Modele macro in ec monetara Cap3.doc
-
Upload
anaverronica2311 -
Category
Documents
-
view
294 -
download
0
Transcript of Modele macro in ec monetara Cap3.doc
Modele macroeconomice cu economie monetară
Cap. III. Modele macroeconomice cu economie monetară
III. 1. Modelul monetarist standard al lui Friedman
Pornind de la concepţia a teoretică privind teoria cantităţii de bani, Friedman a dezvoltat un
model în cadrul căruia sunt utilizate ca ipoteze cele patru propoziţii prezentate mai u.
Modelul lui Friedman este alcătuit din două blocuri: un bloc al sectorului economiei reale şi
unul al sectorului economiei monetare.
Ecuaţiile modelului unt următoarele:
Sectorul economiei reale
, 0 < c < 1 (3.1.)
, (3.2.)
(3..3.)
Sectorul economiei monetare
(3.4.)
(3.5.)
(3.6.)
Sectorul economiei reale este descris, deci, de o funcţie de consum (3.1.), o funcţie a
investiţiilor (3.2.) şi o condiţie de echilibru a pieţei bunurilor şi serviciilor (3.3.). Funcţia
consumului (3.1.) arată că consumul real C / p este proporţional cu venitul real Y / p. Funcţia de
investiţii (3.2.) exprimă faptul că investiţiile reale I / p cuprind o parte autonomă A, reprezentând
suma dintre investiţiile private şi cele publice independente de rata dobânzii şi o componentă i r r
care depinde de rata dobânzii. Aici ir reprezintă parametrul de senzitivitate a investiţiilor reale la
nivelul ratei dobânzii. El este negativ deoarece între investiţii şi rata dobânzii există un raport invers
proporţional.
Condiţia de echilibru (3.3.) spune că venitul naţional real este egal cu suma cheltuielilor
reale planificate pentru bunuri de consum şi investiţii.
Sectorul economiei monetare este descris de următoarele trei ecuaţii. Relaţia (3.4.) exprimă
cererea de bani ca sumă a două componente: cererea tranzacţională my Y / p şi cererea speculativă,
Modele macroeconomice cu economie monetară
mr r. Cererea tranzacţională este proporţională, deci, cu mărimea venitului naţional real în timp ce
cererea speculativă depinde de nivelul ratei dobânzii. Aici my reprezintă parametrul de senzitivitate
al cererii reale în timp ce mr reprezintă senzitivitatea cererii de bani la nivelul ratei dobânzii.
Relaţia (3.5.) arată că oferta de bani MS este dată exogen la nivelul M* în timp ce relaţia
(3.6.) exprimă condiţia de echilibru de pe piaţa monetară.
Modelul conţine şase ecuaţii dar şapte variabile (C, I, Y, MD, MS, p, r) deci este
nedeterminat. Astfel de problemă este rezolvată în teoria clasică introducând o nouă ecuaţie care
permite determinarea venitului real:
(3.7.)
unde Y* este dat exogen. Aici Y* reprezintă nivelul de echilibru al venitului real sau nivelul
de ocupare deplină, şi este stabilit prin sistemul walrasian al ecuaţiilor cererii şi ofertei, precum şi al
condiţiilor de echilibru ale pieţei bunurilor şi serviciilor.
Dacă nivelul venitului real este dat, atunci modelul (3.1.) – (3.6.) pate fi rezolvat recursiv în
modelul următor:
Din ecuaţiile (3.1.) – (3.3.) rezultă că
şi de aici:
(3.8.)
care reprezintă ecuaţia IS a modelului.
Din ecuaţiile (3.4.) – (3.6.) obţinem mai întâi
şi de aici:
(3.9.)
Ecuaţia (3.9.) reprezintă ecuaţia LM a modelului.
Deoarece Y / p = Y* conform (3.7.), putem înlocui valoarea venitului real în (3.8.) şi (3.9.)
şi obţinem:
Modele macroeconomice cu economie monetară
Din relaţiile de mai sus putem obţine, acum, uşor rata dobânzii de echilibru r 0 şi nivelul
preţurilor de echilibru p0:
Se observă că în timp ce rata dobânzii se determină în sectorul real al economiei, utilizând
curba IS, nivelul preţurilor decurge din sectorul monetar al economiei, respectiv din curba LM.
Apare, astfel, o dihotomie în determinarea preţurilor: preţurile relative, inclusiv rata
dobânzii sunt determinate de raportul dintre cererea agregată şi oferta agregată în timp ce nivelul
preţurilor este dat de relaţia dintre cererea de bani şi oferta de bani.
Şcoala macroeconomică keynesiană a rezolvat această problemă făcând ipoteza că nivelul
preţurilor este determinat în afara sistemului.
Soluţia lui Friedman la problema ecuaţiei absente este introducerea unei ecuaţii prin care
este dată rata dobânzii.
El propune următoarea relaţie:
r = re + πe (3.14.)
unde re este rata anticipată a dobânzii iar πe este rata anticipată a inflaţiei.
Dacă notăm cu ye rata aşteptată de creştere a venitului nominal, atunci:
ye = πe + xe (3.15.)
unde xe este rata aşteptată de creştere a venitului real.
Înlocuind πe = ye - xe în ecuaţia (3.14.) obţinem:
r = re + (ye – xe) = (re – xe) + ye (3.16.)
Friedman a considerat că diferenţa dintre rata aşteptării a dobânzii şi rata anticipată de
creştere a venitului real este constantă, deci:
re – xe = R0 (3.17.)
în aceste condiţii, obţinem:
r = R0 + ye (3.18.)
Deci rata dobânzii reprezintă o sumă dintre o constantă şi rata aşteptată de creştere a
venitului nominal, variabilă care nu este explicitată în cadrul modelului. În continuare, modelul
monetarist mai exact blocul monetar al acestuia este modificat în aşa fel încât să poată fi determinat
ye.
Avem:
Modele macroeconomice cu economie monetară
Ecuaţia (3.19.) reprezintă funcţia cererii de bani, m (r) reprezentând rata de creştere a cererii
de bani care variază invers proporţional cu rata dobânzii.
Conform ecuaţiei (3.20.), oferta de bani este exogenă. Toate variabilele endogene şi exogene
sunt funcţii de timp.
Ecuaţia (3.21.) este condiţia de echilibru a pieţei monetare iar ecuaţia (3.22.) este ecuaţia
(3.18.).
Din (3.19.) – (3.21.) obţinem imediat:
(3.23.)
sau
(3.24.)
unde V(t) = 1 / m(t) este viteza de circulaţie a banilor.
Ecuaţiile (3.22.) şi (3.23.) permit determinarea la orice moment de timp t a venitului
nominal Y(t).
Friedman ezită să explice ecuaţia sa referitoare la rata dobânzii şi sectorului real pentru ca
aceasta ar implica o rată reală a dobânzii constantă (mai exact o diferenţă constantă între rata reală a
dobânzii şi rata reală de creştere economică). Cum cererea de bani este influenţată în principal de
rata inflaţiei şi de mărimea venitului real, ipoteza unei rate reale a dobânzii contante nu denaturează
funcţionarea sistemului monetar. În sectorul real, însă, o asemenea ipoteză exclude o determinantă
economică centrală a comportamentului economiilor şi investiţiilor. De aceea, Friedman şi-a limitat
analiza la formularea unei teorii monetare a venitului nominal, lăsând nerezolvată problema
împărţirii acestuia între economii şi investiţii.
Mai mult, după cum a arătat Tobin, modelul monetarist static are anumite proprietăţi care îl
fac mai mult “neokeynesian”. Astfel, dacă cheltuielile guvernamentale cresc, (deci creşte A din
curba IS), venitul real Y / p creşte cu mărimea totală a efectului de multiplicare, în timp ce rata
dobânzii rămâne fixată datorită ecuaţiei de determinare (3.23.). În schimb, dacă oferta de bani MS
creşte, curba IS rămâne neschimbată ca şi curba LM. În schimb, nivelul preţurilor p va creşte în
acelaşi ritm cu MS astfel încât cererea de bani MD să nu fie afectată. De aici concluzia care se
Modele macroeconomice cu economie monetară
regăseşte şi la neokeynesieni conform căreia numai politica fiscală afectează producţia şi ocuparea
forţei de muncă, în timp ce politica monetară este ineficientă.
III. 2. Modelul monetarist dinamic al lui I. Vanderkamp (1975)
Acest model monetarist include trei componente de bază: ecuaţia cantităţii de bani, curba lui
Phillips şi legea lui Okun. Caracterul monetarist al modelului este dat de faptul că rata expansiunii
monetare influenţează rata inflaţiei, iar prin intermediul curbei lui Phillips se face legătura dintre
blocul economiei monetare şi cel al economiei reale.
Modele macroeconomice cu economie monetară
În acest model, un impuls monetar (din o creştere neaşteptată a ofertei de bani) generează o
creştere a ratei de creştere reale peste rata anticipată, ceea ce duce la diminuarea ratei şomajului,
care determină, mai departe o creştere a ratei inflaţiei (legea Okun). La rândul său rata diminuată a
şomajului duce la o creştere a ratei inflaţiei (curba lui Phillips). Această creştere este egală exact cu
diferenţa dintre rata de expansiune monetară şi rata creşterii reale ponderată cu elasticitatea cererii
de bani în funcţie de venit.
Modelul lui Vanderkamp costă din trei ecuaţii:
Ecuaţia (3.41.) reprezintă ecuaţia monetaristă a cantităţii de bani. Aici m t este rata
expansiunii monetare (creşterii cantităţii de bani), xt reprezintă rata de creştere a venitului real iar π t
– rata inflaţiei.
Ecuaţia (3.42.) reprezintă o versiune liniarizată a curbei Phillips. Rata inflaţiei π t este legată
direct proporţional de rata anticipată a inflaţiei πet şi invers proporţional cu diferenţa dintre rata
şomajului ut şi rata naturală (de echilibru) a şomajului ue.
În sfârşit, ecuaţia (3.43.) reprezintă legea lui Okun conform căreia creşterea ratei de creştere
a şomajului este invers proporţională cu decalajul dintre rata creşterii reale x t şi rata anticipată a
creşterii xet.
Modelul are ca variabile endogene rata creşterii reale xt, rata inflaţiei πt şi rata şomajului ut.
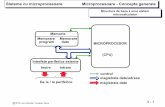
Vanderkamp a dat acestui model o soluţie grafică prezentată în continuare (Figura 1).
În cadranul I al graficului, funcţia R0 reprezintă o curbă Phillips liniară în care aşteptările
inflaţioniste πe = 0. Intersecţia curbei Phillips cu axa Ou determină rata naturală (de echilibru) a
şomajului ue .
În cadranul II e reprezintă grafic ecuaţia cantităţii de bani.
R0FF1
x = xe III
Modele macroeconomice cu economie monetară
Figura 1
Dreptele FFo şi FF1 corespund a două valori diferite a ratei de creştere a ofertei de bani, m0
şi, respectiv, m1. Fiecare punct aflat pe dreptele FF exprimă, deci, o combinaţie posibilă (π, x)
corespunzătoare unei rate de creştere a cheltuielilor nominale. Dreapta verticală x = xe este rata
constantă de creştere echilibrată a venitului real.
Cadranul IV conţine o reprezentare grafică a legii lui Okun. Dreapta OK reprezintă curba
Okun în starea iniţială. Ea arată ratele şomajului care corespund unor rate alternative ale creşterii
reale. Cum curba lui Okun este o ecuaţie cu diferenţe de ordinul I, ea se deplasează către stânga
atunci când rata şomajului scade în urma unei creşteri neaşteptate a ratei de creştere a venitului real
(în figura 1 distanţa ).
Cadranul III transferă valorile lui x din cadranul II în cadranul IV.
În starea staţionară, sistemul economic este caracterizat de următoarele relaţii:
(3.44.)
FF0
x = xe
xe
xe
ue
πA
xA
xA
x1x
x
uAu
A’
A”
A
OK
O
IIIIV
Modele macroeconomice cu economie monetară
În acest caz, rata constantă de creştere a ofertei de bani m0 (aparţinând dreptei FF0) este
utilizată complet pentru finanţarea creşterii economice reale, xe. Rata şomajului corespunde ratei
naturale ue aflată, cum am arătat, la intersecţia dintre R0 şi abscisa Ou.
Să presupunem acum că oferta de bani înregistrează o accelerare, deci rata de creştere a
ofertei de bani sporeşte de la m0 la m1.
Să analizăm ce se întâmplă în acest caz pe termen scurt cu sistemul economic, “termenul
scurt” desemnând aici faptul că în cursul proceselor de ajustare care se declanşează nu are loc nici o
modificare în rata aşteptărilor inflaţioniste (πe rămâne tot timpul egal cu zero).
În figura 1, creşterea lui m0 la nivelul m1 deplasează curba FF din cadranul II de la poziţia
FF0 în poziţia FF1. Primul efect este o sporire a ratei de creştere a venitului real de la x e la xA (mai
mare decât xe corespunzător stării staţionare), o reducere a ratei şomajului la uA şi o creştere a
inflaţiei la πA. Această nouă stare este reprezentată în figură prin punctele A, A’ şi A”.
Analizând mai amănunţit această nouă stare, observăm că acceleraţia monetară (creşterea
ratei de creştere a ofertei de bani de la m0 la m1), concretizată în deplasarea dreptei FF0 la FF1 a
produs o acceleraţie neanticipată a ratei de creştere reale (a cheltuielilor reale) de mărime xA – xi.
Această creştere este transferată în cadranul IV, dând de-a lungul curbei OK a lui Okun, punctul A’
corespunzător unei rate a şomajului uA < ue. În cadranul I, rata mai redusă a şomajului duce, prin
intermediul curbei lui Phillips la o rată pozitivă a inflaţiei, πA. În cadranul al II-lea, punctul A de pe
dreapta FF1 arată divizarea ratei de creştere a venitului nominal x1 într-o componentă reală xA şi o
componenta inflaţionistă x1 – xA = πA .
Să dăm, în continuare, o exprimare matematică a acestor efecte pe termen scurt.
Se observă că modelul (3.41.) – (3.43.) poate fi rescris în următoarea formă:
sau, sub formă matriceală:
Modele macroeconomice cu economie monetară
De aici obţinem sistemul de ecuaţii liniare cu diferenţe:
Iniţial, se presupune că ut-1 = ue ceea ce face ca ultimii termeni din partea dreaptă a ecuaţiilor
(3.48.) – (3.50.) să fie zero. În aceste condiţii, o acceleraţie monetară, deci o creştere a ritmului de
creştere a masei monetare peste xe + πe va determina, simultan, o creştere a lui xt şi πt şi o diminuare
a lui ut .
Noua rată a şomajului devine atunci ut-1 = uA < ue , altfel spus în cadranul IV curba lui Okun
se deplasează spre stânga, corespunzător noii distanţe de pe ordonată uA = -a (x – xe) (vezi figura 2).
În urma noii poziţii a curbei lui Okun noua reprezentare a sistemului economic este
dreptunghiul (B,B’,B”, ). În această etapă, noua stare e caracterizează printr-o diminuare a
diferenţialei de creştere până la xB – xe, printr-o rată sporită a inflaţiei πB (corespunzătoare
punctului B’ din cadranul al II-lea). Deoarece creşterea ofertei de bani rămâne constantă, inflaţia
sporită determină o diminuare a ratei de creştere a economiei reale până la valoarea xB (punctul B
din cadranul I) şi, în consecinţă, o rată mai scăzută a şomajului, uB = – a(xB – xe).
Acum, curba lui Okun e deplasează din nou spre stânga, în poziţia OK2 , noua reprezentare
a sistemului economic fiind dreptunghiul (C, C’, C”, ), completat cu curba corespunzătoare a lui
Okun, OK2 , unde termenul constant al curbei este dat de rata şomajului uB.
Deplasarea de la A’ la G’ de-a lungul curbei lui Phillips se realizează în condiţiile unei rate
descrescânde a şomajului. Deplasarea corespondentă de la A la G pe dreapta FF1 redă variaţia
componentelor ratei nominale de creştere a venitului în favoarea ratei inflaţiei.
FF1
x = xe
π
IIIR
Modele macroeconomice cu economie monetară
Figura 2
Dinamica proceselor de ajustare este determinată de deplasarea curbei lui Okun. Atât timp
cât această curbă se deplasează către stânga nu se poate ajunge la echilibru deoarece se modifică
atât rata inflaţiei cât şi rata şomajului. Curba lui Okun va continua să e deplaseze atât timp cât
diferenţa xt – xe este pozitivă (adică distanţele sunt nenule) sau, altfel spus, atât timp
cât ritmul de creştere a venitului real manifestă o acceleraţie neaşteptată.
Vom analiza acum punctele G, G’, G”, G din figura 2. Din primul cadran putem determina
corespondentele ritmului de creştere a venitului nominal (xG , πG). Deoarece, acum, xG – ue = 0 nu
mai avem o acceleraţie neaşteptată a ritmului de creştere a venitului. În cadranul IV, G” se află la
intersecţia curbei lui Okun OKG cu dreapta x = xe astfel încât, în acest punct, legea lui Okun nu mai
R0
FF0
x = xe
ue
πA
xB
xA
xAx uA u
A’
A”
A
OK
O
III IV
C
B
G G1
xG = xe
xG = xe
xC
xC
xB
G’
C’
B’
OK1OK2
OK3
uBuCuG
OK3
Modele macroeconomice cu economie monetară
acţionează şi curba lui Okun nu mai rămâne stabilă. Punctul G” reprezintă un punct de echilibru
pentru piaţa forţei de muncă iar rata corespondentă a şomajului uG nu e mai modifică.
Atunci echilibrul pe termen scurt se caracterizează prin următoarele relaţii:
(3.51.)
Dacă aşteptările inflaţioniste nu sunt revizuite, atunci curba lui Phillips rămâne stabilă şi
predomină un echilibru pe termen scurt. Acest echilibru este caracterizat de o rată mai ridicată a
inflaţiei, π, o rată mai redusă a şomajului, u dar aceeaşi rată stabilă de creştere reală x e ca şi înaintea
impulsului monetar.
Creşterea ratei de creştere a ofertei de bani (sporirea cheltuielilor nominale) determină,
deci, o accelerare temporară a creşterii care induce o creştere a ratei inflaţiei şi o diminuare a
salariilor reale. În noua stare de echilibru predomină o rată mai înaltă a inflaţiei şi acelaşi ritm al
creşterii reale, precum şi un nivel mai ridicat al ocupării forţei de muncă şi o valoare crescută a
PNB real. Acest echilibru pe termen scurt poate persista numai până în momentul în care aşteptările
inflaţioniste (în special cele reflectate de salariile nominale) sunt ajutate la rata efectivă a inflaţiei.
Putem presupune, de exemplu, că procesul de ajustare a aşteptărilor este descris de
modelul aşteptărilor adaptive.
adică rata aşteptată a inflaţiei variază proporţional cu eroarea de previziune πt – πet-1.
Pe termen lung, rata aşteptată a inflaţiei nu poate rămâne zero dacă rata efectivă a inflaţiei
depăşeşte valoarea zero. Dacă s-ar întâmpla acest lucru, ar fi contrazisă ipoteza comportamentului
raţional al agenţilor economici.
Conform ecuaţiei (3.52.), rata aşteptată a inflaţiei πet va începe să crească şi va continua să se
mărească până când πe = πG . Pe graficul din figura 2, acest proces de ajustare a aşteptărilor
inflaţioniste implică o deplasare a curbei lui Phillips de la R0 la R. În această nouă stare stabilă, nu
vor mai apare surprize şi valorile efective ale variabilelor sistemului corespund întocmai valorilor
lor anticipate. Starea este descrisă, deci, de relaţiile:
(3.53.)
Modele macroeconomice cu economie monetară
Deosebirea dintre echilibrul pe termen lung, caracterizat de punctul (G, G1, G2, ) şi
echilibrul pe termen scurt (G, G’, G”, ) constă în faptul că primul, diferenţa de creştere anticipată
(x – xe) cât şi efectul real aspra pieţei muncii au dispărut.
Ca urmare a deplasării în sus şi spre dreapta a curbei lui Phillips, deplasare cauzată de o rata
anticipată a inflaţiei mai mare, rata şomajului creşte din nou până când, în punctul G2, rata naturală
a şomajului, ue este din nou atinsă. Deplasarea curbei lui Phillips antrenează şi o deplasare a curbei
lui Okun, pe care o vom studia în continuare.
La echilibrul pe termen lung, rata inflaţiei este complet anticipată şi este, ca şi în cazul
echilibrului pe termen scurt, egală cu diferenţă dintre rata de expansiune a ofertei de bani m şi
ritmul xe al creşterii reale.
Această analiză arată că un impuls monetar (diferit ca o deplasare de la FF 0 la FF1)
determină o accelerare neaşteptată a creşterii economice care dispare în cursul procesului de
ajustare pe termen scurt, prin deplasările ecuaţiei lui Okun.
În timpul procesului de ajustare pe termen lung, care duce la deplasări ale curbelor lui
Phillips şi Okun, rata şomajului creşte din nou până la nivelul celei naturale.
Spre deosebire de procesul de ajustare pe termen scurt, analizat mai sus, procesul de ajustare
pe termen lung implică a deplasare a curbei lui Phillips datorită unei variaţii a ratei anticipate a
inflaţiei, πe. Trăsăturile esenţiale ale acestui proces sunt următoarele:
a) Poziţia curbei lui Phillips depinde de rata decalată a inflaţiei aşteptate π e-1 şi de eroarea de
previziune π-1 – πe . Dacă are loc o accelerare neanticipată a ratei inflaţiei, curba lui Phillips se
deplasează ascendent dacă π-1 – πe < 0;
b) Poziţia curbei corespondente a lui Okun este dată de rata decalată a şomajului, u -1 . Dacă
rata şomajului creşte, deci u-1 > u-2 , curba lui Okun se deplasează către dreapta; în caz contrar către
stânga;
c) În situaţia în care curbele lui Phillips şi Okun pentru o anumită perioadă sunt determinate
de valorile anterioare, rata creşterii reale x (mai precis g = x – xe ) şi curba lui Okun determină
atunci rata corespondentă a şomajului. Introducând în expresia curbei lui Phillips rata şomajului,
obţinem rata efectivă a inflaţiei.
Traiectoriile de evoluţie ale variabilelor endogene πt , πet şi gt = xt – xe sunt determinate de
rezolvarea sistemului de ecuaţii cu diferenţe finite (3.48.) – (3.50.) la care e adaugă o ipoteză
privind formarea aşteptărilor inflaţioniste, de exemplu:
(3.53.)
Modele macroeconomice cu economie monetară
În plus trebuie specificate aşteptările privind rata şomajului, respectiv rata de creştere, u e şi
xe care rămân contante pe orizontul de timp considerat.
Valorile iniţiale sunt date de echilibrul pe termen scurt, căruia îi corespund anumite valori
numerice pentru πG = π0; xG = xe şi uG = u0.
În aceste condiţii, sistemul compus din ecuaţiile (3.48.) – (3.50.) şi (3.52.) la care se adaugă
condiţiile iniţiale poate fi rezolvat, generând traiectoriile de evoluţie ale variabilelor endogene
amintite.
Se arată uşor că procesul de ajustare este stabil (deci oscilaţiile sunt amortizate) dacă:
(3.54.)
în timp ce aşteptările inflaţioniste sunt convergente către cele date de rata reală a inflaţiei
dacă 0 < θ < 1.
Evoluţia oscilantă a variabilelor endogene este determinată de condiţia:
(3.55.)
caz în care sistemul de ecuaţii cu diferenţe finite are rădăcini complexe.
III.3. Modelul monetarist dinamic cu aşteptări raţionale (Frish, 1982)
Vom introduce, pornind de la modelul lui Vanderkamp, un model dinamic cu aşteptări
raţionale.
Modelul este alcătuit din următoarele ecuaţii:
Modele macroeconomice cu economie monetară
Aici gt = xt – xe exprimă abaterea ratei reale de creştere a venitului de la valoarea de
echilibru iar εit, i = 1, 2, 3, sunt variabile aleatoare independente între ele şi faţă de celelalte
variabile ale modelului având media 3e+0 (E (εit) = 0) şi dispersie constantă (var (εi
t) = ct.).
Se remarcă faptul că în legea lui Okun (3.58.), termenul ut-1 este înlocuit cu ue ceea ce
presupune că o accelerare a creşterii reale poate împinge rata şomajului sub valoarea sa naturală de
echilibru ue , în timp ce în modelul lui Vanderkamp rata şomajului cobora sub nivelul să din
perioada anterioară.
În modelul (3.56.) – (3.58.) variabilele endogene sunt πt – rata curentă a inflaţiei, gt –
abaterea creşterii reale faţă de trend şi ut – rata şomajului. Variabilele exogene sunt mt – rata de
creştere a ofertei de bani; πet – rata aşteptată a inflaţiei, ue
– rata naturală (de echilibru) a şomajului,
εit (i = 1, 2, 3) – variabilele aleatoare şi xe – rata creşterii reale în condiţii de echilibru.
Pentru a determina sistemul de ecuaţii cu diferenţe vom pune modelul (3.56.) – (3.58.) sub
forma:
(3.59.)
care mai poate fi scris matriceal:
(3.60.)
De aici:
Modele macroeconomice cu economie monetară
(3.61.)
şi efectuând înmulţirile:
Vom nota termenii aleatori ai ecuaţiilor (3.62)-(3.64) cu ω1t , ω2
t şi, respectiv ω3t, deci:
(3.65.)
Modelul cu aşteptări raţionale se scrie:
Se poate observa acum că variabilele endogene gt şi ut sunt influenţate atât de diferenţa (mt –
xe – π2t) cât ş de termenii aleatori ω1
t , ω2t şi ω3
t.
Modelul de mai us trebuie completat cu o ipoteză privind generarea ratei de creştere a
ofertei de bani mt. În modelul cu aşteptări raţionale acest lucru se face prin introducerea unei reguli
de politică monetară, de exemplu o regulă feed-back liniară de forma:
(3.69.)
Modele macroeconomice cu economie monetară
Deci mt depinde de o componentă autonomă μ0, de abaterea ratei de creştere reală de la rata
naturală de creştere, gt, de rata inflaţiei πt, ambele decalate cu o perioadă, precum şi de o variabilă
aleatoare εt de medie zero şi dispersie contantă.
Primii trei termeni din partea dreaptă a ecuaţiei (3.69.) formează partea sistematică a regulii
de politică monetară în timp ce termenul aleator εt reprezintă aspectul nesistematic al acestei reguli.
Friedman considera μ1 = μ2 = 0, deci recomanda o regulă monetară pasivă mt = μ0. Alţi
monetarişti recomandau alegerea lui μ1 şi μ2 la valori negative, fiind adepţii unei politici monetare
anticiclice.
O ipoteză esenţială a teoriei aşteptărilor raţionale este că agenţii economici cunosc
componenta sistematică a ratei de creştere a ofertei de bani şi ţin cont de ea. Dacă notăm cu Ωt-1
informaţia totală existentă la nivelul agenţilor economici atunci aşteptările acestora în legătură cu mt
pot fi scrise:
(3.70.)
Ecuaţia (3.69.) poate fi scrisă sub forma :
(3.71.)
Ecuaţia (3.71.) arată că rata de creştere a ofertei de bani conţine o componentă sistematică
E(mt / Ωt-1) şi o componentă aleatoare εt care nu poate fi prevăzută.
Să arătăm, în continuare, cum se formează aşteptările raţionale din cadrul componentei
sistematice. Începem cu aşteptările inflaţioniste. Ţinând seama de faptul că E(εit) = 0, i = 1, 2, 3 şi
aplicând operatorul de aşteptare ecuaţiei (3.63.) obţinem:
(3.72.)
De aici rezultă:
(3.73.)
care exprimă inflaţia anticipată raţional πet luând în considerare toate variabilele endogene şi
exogene precum şi interdependenţele dintre ele. Rata inflaţiei anticipată raţional reprezintă, deci,
diferenţa dintre componenta sistematică a ratei de creştere a ofertei de bani E(mt / Ωt-1) şi tendinţa
ratei de creştere a economică reală, x2.
O creştere a ratei aşteptată de expansiune a ofertei de bani generează imediat o creştere a
ratei aşteptate a inflaţiei.
Dacă înlocuim, acum, ecuaţia (3.73.) în (3.63.) şi ţinem cont de relaţia (3.71.) obţinem:
Modele macroeconomice cu economie monetară
(3.74.)
Rata curentă a inflaţiei πt ete alcătuită din două componente: rata anticipată a inflaţiei
(primul termen din partea dreaptă) şi o componentă sistematică a ofertei de bani, determinată ca
diferenţă dintre rata efectivă a ofertei de bani mt şi rata anticipată a acesteia E(mt / Ωt-1).
Din ecuaţia (3.74.) rezultă imediat:
(3.75.)
Această ecuaţie arată faptul că diferenţa dintre rata curentă a inflaţiei şi rata anticipată a
acesteia este dependentă de eroarea de previziune a ofertei de bani, termenul de proporţionalitate
fiind ab / (1 + ab), la care se adaugă şi o componentă aleatoare ε2t .
În continuare să determinăm influenţa aşteptărilor raţionale asupra sectorului economiei
reale.
Pentru aceasta vom înlocui ecuaţia (3.73.) care dă inflaţia anticipată în ecuaţiile (3.62.) şi
(3.64.) şi obţinem:
Ecuaţiile (3.76.) şi (3.77.) dau ecuaţiile ratei şomajului ut şi ratei de creştere a producţiei
reale gt. Se poate observa că amândouă aceste rate sunt influenţate de eroarea de previziune a ofertei
de bani mt – E(mt / Ωt-1). De exemplu, o diferenţă mt – E(mt / Ωt-1) > 0 va determina, prin
intermediul unei abateri πt - πet > 0 coborârea lui mt sub ue în ecuaţia (3.76.) şi creşterea lui gt în
ecuaţia (3.77.).
Dar aceste efecte reale sunt influenţate şi de o componentă sistematică εit şi de aceea nu pot
fi folosite într-o politică economică. Deci sectorul real al economiei este independent de politica
monetară anticipată. În cadrul modelului, rata aşteptată a inflaţiei reflectă perfect orice schimbare a
componentei sistematice a creşterii ofertei de bani ceea ce sporeşte rata curentă a inflaţiei, fără a
avea, însă, repercusiuni asupra sectorului real. O astfel de concluzie poartă numele de “teza
ineficienţei politice” şi asupra sa au fost purtate polemici îndelungi între monetarişti şi keynesişti.
Modele macroeconomice cu economie monetară
III.4. Modelul neoclasic cu aşteptări raţionale al lui McCallum - Whitaker
Înainte de a prezenta modelul este necesar să precizăm anumite caracteristici generale ale
aşteptărilor raţionale. Pentru aceasta ne vom imagina o variabilă economică Y ale cărei valori sunt
determinate de următorul proces stochastic, incluzând un element imprevizibil:
(3.78. )
unde λt ~ N(0, σ2λ), iar valoarea sa în perioada t este necunoscută: nu face parte din It-1
(mulţimea informaţională de la momentul t-1).
Este clar că predictor raţional, care se bazează pe procesul determinant al lui Y pentru a
previziona la sfârşitul perioadei t-1 valoarea lui Y în perioada curentă t, trebuie să-şi formeze o
aşteptare în privinţa valorii pe care o va lua eroarea λ în perioada curentă:
(3.79.)
unde reprezintă aşteptarea raţională asupra lui Yt-1, formată la
momentul t-1 şi este dată de media condiţionată a lui Yt în raport cu informaţia disponibilă la
momentul t-1.
adică:
iar eroarea de aşteptare este dată de relaţia :
(3.80. )
deci de diferenţa dintre valoarea reală, la momentul t1, a lui Y şi cea previzionată la
momentul t-1.
3.3.1. Caracteristicile generale ale aşteptărilor raţionale
Mai multe concluzii rezulta din faptul că dacă procesul care îl determină pe Y este înţeles,
eroarea unei aşteptări raţionale este aceeaşi cu componenta aleatoare a acelui proces:
a) eroarea medie este zero. Odată ce procesul lui Y este stocastic, aşteptările raţionale nu
mai au caracteristica implauzibilă de a fi exacte în fiecare perioadă. În loc de aceasta au
caracteristica mai slabă de a fi corecte în medie.
Modele macroeconomice cu economie monetară
b) Nu va exista nici un model de comportament pe care să-l urmeze eroarea
aşteptărilor raţionale. Dacă se observă că ν urmează o lege de comportament, de
exemplu:
(3.81)
atunci indivizii îşi vor forma aşteptările asupra lui λ în funcţie de această lege. Rezultă că aşteptările
raţionale asupra lui Y vor fi în medie corecte, iar eroarea (acum εt) nu va urma nici o lege de
comportament.
Ipoteza aşteptărilor raţionale sugerează astfel că, atât timp cât procesul ce determină
variabila nu se schimbă, nu se va schimba nici metoda de formare a aşteptărilor. Altfel, metoda se
va schimba odată cu el.
c)aşteptarea raţională este, în general, cea mai bună aşteptare care se poate forma. λ
are variantă finită, ceea ce fixează o limită superioară erorii de previziune. Dacă avem aşteptări
raţionale, eroarea în fiecare perioadă va fi egală cu λt . atunci, pentru orice alt model de estimări,
acurateţea pe o anumită perioadă de timp nu poate să depăşească σλ2 , astfel încât aşteptările
raţionale sunt cea mai eficientă metodă de previzionare: varianţa erorilor de estimare va fi
întotdeauna mai mică în acest caz decât orice alt model de previziune.
3.3.2. Descrierea modelului
Modelul utilizat de McCallum şi Whitaker este o versiune simplificată a modelului discret
Sargent – Wallce (1975).
1.Oferta agregată:
(3.82.)
cu:
yt reprezentând logaritmul outputului agregat din perioada t
pt reprezentând logaritmului nivelului preţului agregat din perioada t
Et-1 pt = E(pt/ It-1) aşteptarea asupra nivelului mediu al preţului în perioada t (pt), folosind
informaţia disponibilă la momentul t-1.
ut reprezentând o variabilă aleatoare generată de un proces de tip zgomot alb
a1> 0, 0< a2 < 1
Modele macroeconomice cu economie monetară
Termenul al treilea presupune faptul că deviaţiile outputului de la nivelul capacităţii
productive determinate de erorile de aşteptare pot persista mai multe perioade (datorită costurilor
reale de ajustare).
2.Funcţiile IS şi LM:
(IS)
(LM)
unde:
Et-1 (pt+1 – pt) – aşteptarea formată la momentul t-1 privind diferenţa dintre preţul la
momentul t+1 şi preţul la momentul t
gt – logaritmul cheltuielilor guvernamentale
zt – logaritmul taxelor reale
mt – logaritmul ofertei de bani
rt – rata nominală a dobânzii
vt, et – variabile aleatoare generate de procese independente de tip zgomot alb
b1, b3, c2 < 0 iar b2, c1 > 0
De notat faptul că diferenţa gt – zt reprezintă logaritmul raportului dintre cheltuielile
guvernamentale şi taxe, astfel încât, dacă este pozitivă, ea va implica un deficit bugetar
Apariţia lui zt în ecuaţia curbei (IS) susţine viziunea în care finanţarea cheltuielilor
guvernamentale cu ajutorul taxelor în loc de obligaţiuni va diminua cererea agregată.
Pentru a completa modelul trebuie să specificăm modul în care sunt determinate politicile gt,
zt şi mt. Astfel, vom presupune că autoritatea monetară menţine rata taxelor neschimbată în raport
cu condiţiile economice, astfel încât veniturile din taxe depind doar de outputul curent:
zt = τ1 · yt,
unde:
τ1 – reprezintă parametrul ratei de taxare (= raportul între rata marginală şi rata medie)
τ1 > 0