File d1332352347file4f6a155b62379
-
Upload
adina-georgiana -
Category
Engineering
-
view
114 -
download
1
Transcript of File d1332352347file4f6a155b62379
Tehnici (Transformate) utilizate in procesarea semnalelor analogice
• Convolutia: – concept de baza in procesarea
semnalelor care afirma ca semnalul de IN poate fi combinat cu diferite functii ale sistemului pt. determinarea marimii de IE;
• Transformata Fourier– Descompune un semnal intr-un sir de
componente sinusoidale de frecvente diferite, facand trecerea din domeniul frecventa in domeniul timp, realizand calculul amplitudinii si fazei semnalului transformat
• Transformata Laplace– Transformata Fourier generalizata care
transforma un semnal sau un sistem intr-un nr. complex
( ) ( ) ( ) ( ) ( )b
a
y t x h t x h t dτ τ τ= × × = × − ×∫
( ) ( ) j tX j x t e dtωω∞
−
−∞
= ×∫
( ) ( ) stX s x t e dt∞
−
−∞
= ×∫
Analiza Fourier
• Analiza Fourier este extrem de utilă pentru procesarea datelor, deoarece descompune un semnal într-un şir de componente sinusoidale de frecvenţe diferite, făcând trecerea din domeniul timp în domeniul frecvenţă, realizând calculul amplitudinii şi fazei variabilelor (datelor, semnalelor) transformate.
• Pentru eşantionarea datelor vectoriale, analiza Fourier utilizează transformata Fourier discretă (discrete Fourier transform-DFT).
• Transformata Fourier rapidă - FFT (Fast Fourier Transform) este un algoritm foarte eficient pentru calcularea transformatei Fourier, sau a transformatei Fourier discrete (DFT).
Transformata Fourier
• Unealta matematică pentru analiza unui semnal în domeniul frecvenţei care poate lua diferite forme în funcţie de semnalul analizat.
• Ceea ce au în comun aceste semnale este faptul că sunt alcătuite dintr-un număr de componente sinusoidale de frecvenţe diferite, fiecare având o anumită amplitudine şi fază iniţiale.
• Transformata Fourier face conversia unui semnal din domeniul timp într-un semnal discret în domeniul frecvenţei.
• Dacă g(t) este un semnal neperiodic exprimat ca funcţie de timp, transformata Fourier a funcţiei g(t) este dată de expresia integrala:
∑∞
∞−
−= dtftjtgfG )2exp()()( π
Transformata Fourier Rapida-FFT
• Transformata Fourier rapidă (FFT) este o metodă eficientă de calcul a transformatei Fourier discrete.
• Transformata Fourier discretă poate fi exprimată prin relaţia:
• FFT reduce numărul de calcule matematice necesare pentru calculul transformatei Fourier discrete (DFT). De exemplu, dacă o secvenţă are N puncte, pentru calculul DFT sunt necesare N2 operaţii iar pentru calculul FFT sunt necesare doar N/2 log2(N) înmulţiri şi împărţiri complexe.
• FFT poate fi utilizată si pentru calculul spectrului puterii unui semnal, pentru filtrarea digitală a semnalelor sau pentru obţinerea corelaţiei dintre 2 semnale.
∑−
=
−=1
0
)/2exp(][][N
n
NnkjngkG π
Distorsiunea Totala a Armonicilor unui Semnal-THD(Total Harmonic Distorsion)
• Distorsiunea armonică aproximează forma de undă a unui semnal (curent, tensiune, putere etc.) cu fundamentala acestuia.
• Pentru seria Fourier, distorsiunea armonică procentuală, pentru fiecare componentă este dată de una din relaţiile:
%100*...[%]2
1
2
1
3
2
1
2
++
+
=
A
A
A
A
A
ATHD n
%100*...
[%]1
223
22
A
AAATHD n+++
=
Transformata Laplace
• Transformata Laplace a unui semnal in timp continuu x(t) poate fi exprimata prin relatia:
• Poate fi reprezentata in planul s in doua dimensiuni, cu σ de-a lungul axei reale si pulsatia Ω pe axa imaginara.
( ) ( ) stX s x t e dt∞
−
−∞
= ×∫
s jσ= + ×Ω
TehniciTehnici (Transformate) (Transformate) utilizate in procesarea utilizate in procesarea semnalelor digitalesemnalelor digitale
• Corelatia (autocorelatia);• Convolutia (produsul de convolutie);• Transformata Fourier Discreta (TFD-fft);• Transformata z;• Transformata Hilbert;• Transformata Wavelet.
CORELATIA• Permite recunoasterea
sau identificarea semnalelor emise (radar, ECG);
• Pt. un semnal (secventa) de IN x[n] si o secventa data(sablon) h[n] de lungime ct. M, corelatia se defineste:
1
[ ] [ ] [ ( 1) ]0
M
n k n M kk
y h x−
− − +=
= ×∑
CONVOLUTIA
• Este unul dintre cei mai importanti algoritmi utilizati in procesarea numerica a semnalelor;
• La convolutia dintre coeficientii unui sistem liniar si semnalul de IN (x[n]), esantionul curent de IE se obt. ca suma ponderata a ultimelor N esantioane ale semnalului de IN;(pt. calculul esantionului de IE sunt necesare N inmultiri si N-1 adunari);
• Convolutia semnalelor poate fi determinata:– Direct:utilizand formula de def.;– Indirect: utilizand transformata
Fourier (se calculeaza transf. Fourier, se face produsul semnalelor si apoi se calculeaza transformata Fourier inversa);
[ ] [ ] [ ] [ ] [ ]n k n k n ny h x h x−= × = ×∑
Transformata Fourier discreta-TFD
• Ofera informatii despre spectrul de frecventa al unui sistem (spectrul unui semnal discret);
• Este utilizata pt. esantionarea datelor vectoriale (multimea semnalelor armonice in care semnalul discret poate fi descompus);
• Transforma N esantioane ale unui semnal din domeniul timp in N valori complexe din domeniul frecventa;
0
0
1
[ ] [ ]0
[ ] ; 0,1, 2,..N
jn kTenTe TFD n
k
TFD u U u kTe e n−
− Ω ×Ω
== = × =∑
Legatura dintre Transformata Fourier si Transformata Fourier discreta
• Considerand ca tensiunea u[nTe] provine din tensiunea u(t), esantionata cu frecventa fe=1/Te, atunci TFD poate fi privita ca un caz particular al Transformatei Fourier in care:
0
0
1
[ ]0
[ ]
; ;
( ) ( )
( )
e
e e
Njk nTj t
nT ek
e TFD n
t n T dt T k
F j u t e dt u e T
F j T U
ω
ω
ω
ω
∞ −− Ω ×−
=−∞
Ω
= × = = ×Ω
= × → ×
→ ×
∑∫
Transformata Fourier discreta rapida
• Algoritm de calcul f. eficient pt. analiza unui semnal in raport cu frecventa;
• Reduce nr. de calcule matematice de la N2 operatii la N/2 * log2(N);
• Daca aplicam TFD unei secvente de N date, semnalul caruia ii va corespunde spectrul rezultat se obtine multiplicand prin periodicitate aceasta secventa (daca secventa nu contine un nr. intreg de perioade spectrul rezultat nu este corect);
Transformata z
• Este o unealta matematica f. utila pt. analiza si proiectarea semnalelor in timp discret;
• Plecand de la Transf. Fourier in timp discret a unui semnal x[n] si notand variabila complexa z=ejω se obtine transformata z a semnalului:
( ) [ ] n
n
X z x n z∞
−
=−∞= ×∑
Transformarea semnalelor în domeniul frecvenţă
Procesorul de semnal (DSP) nu poate opera cu ambele concepte simultan.
Pentru a calcula ieşirea unui sistem pentru un semnal de intrare dat, trebuie să-i furnizăm o metodă de calcul a rezultatului logică, pas cu pas.
Suntem deci în faţa unei dileme: dacă semnalul de intrare este o serie secvenţială de pulsuri numerice, deci un semnal în domeniul timp şi sistemul este descris prin răspunsul său în frecvenţă, cum va executa DSP –ul acest program ?• Transformăm semnalul de intrare în domeniul frecvenţă;• Transformăm răspunsul sistemului în domeniul timp.
Amândouă tipurile de transformări sunt utilizate în procesarea numerică a semnalului.
Adesea transformăm răspunsul în frecvenţă în domeniul timp pentru a ne permite să construim filtre numerice.
Transformarea semnalelor în domeniul frecvenţă
• Cu filtrele FIR sau IIR producem o reprezentare în domeniul timp a răspunsului filtrului, pe care îl combinăm cu semnalul de intrare pentru a calcula ieşirea rezultantă.
• Altă metodă este de a converti semnalul de intrare în domeniul frecvenţă, care este extrem de util când dorim să înţelegem caracteristicile de frecvenţă ale unui semnal. De exemplu, cunoaşterea răspunsului în frecvenţă a unui canal de telecomunicaţii este extrem de utilă. Aceasta ne permite să decidem care este frecvenţa maximă pe care o putem transmite şi ce distorsiune va căpăta semnalul după străbaterea canalului.
Transformarea semnalelor în domeniul frecvenţă• Alt exemplu este în analiza vorbirii. Prin transformarea
semnalului de vorbire în componente de frecvenţă, putem distinge între vorbitori şi putem determina cuvintele rostite. Aceasta este foarte util în recunoaşterea şi identificarea vorbirii, două aplicaţii care au crescut în interes o dată cu creşterea performanţelor DSP –urilor.
• Alt exemplu foarte evident al transformării unui semnal din domeniul timp în domeniul frecvenţă este în analizoarele de spectru, care sunt acum în uz general în majoritatea laboratoarelor electronice. Analizoarele de spectru pot fi utilizate pentru a examina ieşirea de la senzorii ataşaţi structurilor mecanice, de exemplu: poduri, unde o schimbare semnificativă în răspunsul în frecvenţă poate însemna o solicitare excesivă a unei anume părţi a structurii şi ruperea în viitorul imediat.
Transformarea semnalelor în domeniul frecvenţă
Jean Baptiste Joseph Fourier a obţinut formulele sale clasice în anul 1822 !
În lucrarea lui Fourier intitulată Mémoire sur la propagation de la chaleur dans les corps solides, la paginile 218 și 219, se pot citi următoarele:
Înmul ind ambele păr i cu ț ț
i apoi integrând de la ș la
rezultă:
Transformarea semnalelor în domeniul frecvenţă
Modelul fazoruluiCa un punct de plecare, avem nevoie de o metodă simplă pentru descrierea unui semnal. Vom utiliza modelul fazorului.
Un fazor este de fapt un vector care se roteşte în planul complex, cu o amplitudine A şi o viteză de rotaţie ω rad/sec.
Transformarea semnalelor în domeniul frecvenţă
Dacă luăm un moment instantaneu de timp, putem vedea că semnalul în acel moment, x(t) este dat de:
X(t) = (coordonata reală) + j (coordonata imaginară) = a + jb
unde:
Transformarea semnalelor în domeniul frecvenţă
Cealaltă metodă, este forma polară, unde:
x(t) = A ej(ωt) şi ej(ωt) = cos (ωt) + j sin(ωt)
Transformarea semnalelor în domeniul frecvenţăDescrierea fazorului poate fi cu uşurinţă extinsă la timpul discret sau sisteme numerice, unde semnalul se produce numai la intervale specifice de timp, definite prin intervalul de eşantionare TS:
x(n) = Aej(nωTs)
Astfel în loc de variabila continuă timp t, avem acum o variabilă discretă n, astfel că fazorul avansează în salturi de TS.
Luând oricare dintre cazuri, continuu sau discret, dacă avem o valoarea iniţială pentru x:
x(0) = Aej(α)
Putem obţine forma generală pentru ambele ecuaţii, după cum urmează:
x(t) = Aej(ωt + α) sau x(n) = Aej(nωTs + α)
Aceste simple ecuaţii formează baza tuturor analizelor următoare.
Transformarea semnalelor în domeniul frecvenţă
Modelarea sinusoidelorÎntorcându-ne la descrierea lui ej(ωt) putem să îl rescriem astfel:
ejθ = cosθ + jsinθde asemenea:
e-jθ = cosθ – jsinθ. unde
θ = (ωt + α) sau (nωTS + α)
Din aceste două ecuaţii putem obţine următoarele relaţii:
Transformarea semnalelor în domeniul frecvenţă
Aceasta înseamnă că un semnal general sinus sau cosinus, x(t) poate fi definit ca suma a doi fazori. De exemplu
Astfel semnalul nostru cosinus poate fi reprezentat prin doi fazori care formează o pereche conjugată.
Transformarea semnalelor în domeniul frecvenţă
Aceasta înseamnă că au aceeaşi valoarea reală (a) şi valori egale şi de semn contrar pentru b. Putem calcula forma fazorului a unei forme de undă sinusoidale şi vom găsi că aceasta constă de asemenea într-o pereche conjugată de fazori, însă semnul va fi diferit.
Transformarea semnalelor în domeniul frecvenţă
Să ne reamintim că fazorii noştri se rotesc în oricare direcţie, în sensul acelor de ceasornic sau în sens contrar şi că putem obţine o proprietate foarte interesantă şi anume că toate semnalele reale trebuie făcute din perechi conjugate de fazori, astfel că suma vectorilor va fi întotdeauna legată de axa reală.
Transformarea semnalelor în domeniul frecvenţă• Serii Fourier
Formele de undă mai complicate pot să fie de asemenea împărţite în mai multe forme de undă sinus sau cosinus.
De exemplu, un tren de pulsuri dreptunghiulare constă într-un număr infinit de forme de undă sinusoidale de o amplitudine variabilă.
Astfel, putem descrie orice semnal periodic complex ca o sumă de mai mulţi fazori. O metodă de descriere a semnalului în acest mod este numită serii Fourier, care presupune că setul fazorilor are frecvenţe care sunt multipli de anumite frecvenţe fundamentale, f0 (sau frecvenţe unghiulare ω0)
Transformarea semnalelor în domeniul frecvenţă• Serii Fourier
Orice semnal periodic poate fi reprezentat printr-o serie Fourier cu condiţia ca N să fie destul de mare. Componentele individuale de frecvenţă sunt cunoscute ca şi armonici.
Putem construi modelul Fourier mai general prin utilizarea fazorilor ai căror frecvenţe nu sunt legate armonic care este în general cazul când un semnal complex nu este periodic (majoritatea cazurilor în aplicaţiile reale):
Orice formă de undă arbitrară poate fi reprezentată printr-o serie Fourier de acest tip general.
Serii Fourier Discrete• Acum avem nevoie să translatăm aceste ecuaţii continue în timp
în domeniul discret sau numeric pentru a ne permite să obţinem anumite formule folositoare pentru DSP –uri.
• Analiza de mai sus poate fi extinsă la sisteme cu timp discret. Tot ceea ce e necesar este să înlocuim funcţia continuă t, cu una care progresează în salturi de ω0TS astfel că pentru cazul periodic
Este interesant de remarcat că atunci când saltul fazei pentru armonica de ordinul k este dat de:
k ω0TS = 2πm
unde m este un întreg, faza nu se distinge de cazul când k = 0.
Aceasta se întâmplă deoarece 2 π = 3600 şi are loc când:
Aceasta înseamnă că răspunsul în frecvenţă al unui semnal discret este periodic, cu o perioadă de 1/TS.
Am utilizat acum modelul de fazor simplu pentru a descrie un semnal discret general.
Utilizând această descriere putem merge mai departe să explicăm cum putem face transformarea între domeniile timp şi frecvenţă.
Semnale neperiodice – Transformata Fourier
În aplicaţiile reale, cele mai multe semnale nu sunt periodice, deci trebuie să modificăm seria noastră Fourier ca să cuprindă aceasta. Hai să considerăm seria Fourier generală unde toate frecvenţele sunt legate armonic, deci
ωk = ωk0
Faptul că semnalul final nu este periodic poate fi reprezentat prin
ω0 0
Această ecuaţie pur şi simplu stabileşte că nu există “cel mai mic numitor comun” în frecvenţele tuturor fazorilor noştri separaţi. Când numărul fazorilor tinde către infinit şi suma noastră devine o integrală:
În ecuaţia de mai sus am presupus că amplitudinea semnalului poate fi definită ca o funcţie de frecvenţă (ω), deci x(ω). Ecuaţia “inversă” care defineşte pe x(ω) este dată de:
Astfel, avem acum o ecuaţie care ne permite să calculăm amplitudinea răspunsului unui semnal continuu în domeniul frecvenţă utilizând răspunsul său în domeniul timp. Aceste două ecuaţii sunt numite perechea de transformate Fourier.
Aceste formule sunt foarte utile pentru matematicieni însă, din nefericire, nu este posibil să le implementăm pe un DSP.
Evident, acum este necesar un număr infinit de măsurători pentru a determina funcţia x(ω). În practică, transformatele Fourier nu sunt în realitate calculate; pur şi simplu utilizăm tabelele de perechi de transformate Fourier care se găsesc tipărite în majoritatea cursurilor de matematică sau de DSP
Transformata Fourier discretă (DFT)Pentru a găsi echivalentul discret al transformatei Fourier, trebuie să înlocuim variabila continuă t cu variabila discretă nTS.
În afara intervalului ±π/TS, spectrul se repetă; astfel putem schimba limitele de integrare ωTS şi integrala devine acum:
Transformata inversă este:
Consideratii practicePână acum, am introdus o metodă de descriere a unui semnal care variază în timp, numită modelul fazorului.
Am raportat acest model la formele de undă sinus şi cosinus şi am introdus seriile Fourier, care ne spun că orice semnal periodic poate fi reprezentat printr-un număr de forme de undă sinusoidale raportate armonic.
După ce am făcut seriile Fourier mai generale prin eliminarea relaţiei dintre armonici am aplicat forma discretă a ecuaţiei care în final ne-a dat perechea de DFT.
Astfel acum avem o pereche de ecuaţii care ne va permite să transformăm orice semnal discret între domeniile timp şi frecvenţă, însă cum programăm DSP –ul pentru a face-o DFT ?
Referindu-ne în urmă la ecuaţia DFT pentru x(ω), există două probleme evidente:
• Prima, în lumea reală o adunare infinită nu este posibilă, că nu vom furniza niciodată un răspuns.
• A doua, suntem limitaţi în timp când trebuie să calculăm o ieşire – chiar şi cu un DSP. Astfel, suntem restrânşi în numărul frecvenţelor la care putem face calculele matematice.
• Prima problemă este uşor de depăşit:
Trebuie să luăm doar o secţiune din mărimea de intrare x(n). Aceasta este de obicei referită ca deschidere şi este utilizată în multe alte aplicaţii.
Dacă executăm DFT asupra lui x(n) deschis, spectrul rezultant este dat de:
XN(ω) = X(ω) * W(ω)unde XN(ω) denotă spectrul deschis cu N – numărul de eşantioane utilizate, W(ω) denotă spectrul deschiderii cu * denotă convoluţia dintre W(ω) şi x(ω).
Fereastra ideală ar trebui să aibă un spectru dreptunghiular în domeniul frecvenţă. Spectrul de frecvenţe va fi periodic cu frecvenţa ωS, un spectru dreptunghiular în domeniul frecvenţă implică faptul că nu vom produce nici o interferenţă între buclele adiacente ale răspunsului. Din nefericire, un răspuns în frecvenţă dreptunghiular este practic imposibil de realizat.
• Să presupunem că am ales o funcţie de deschidere. Trebuie să ştim cum are sens să utilizăm numai un număr limitat de frecvenţe şi cât de multe frecvenţe sunt necesare pentru a menţine o suficientă acurateţe. În principiu nu este un răspuns simplu. În general, numărul optim de fazori este egal cu numărul punctelor iniţiale în x(n) deci, N. Calea cea mai simplă ca să ne inaugurăm aceasta este să presupunem că porţiunea noastră deschisă din x(n) constă într-o perioadă dintr-o secvenţă lungă cu perioada NTS şi frecvenţa ωS/N. Dacă facem aceasta putem trata secvenţa ca pe o serie Fourier şi putem vedea că spectrul va consta în N fazori.
Am remarcat mai devreme că spectrul unei DFT este periodic cu perioada ωS, astfel dacă spunem că fazorii sunt separaţi între ei prin δ atunci:
Nδ = ωS
Aceasta ne-a permis să digitizăm scala de frecvenţe astfel că spectrul nostru poate acum fi scris în termeni de k în loc de ω:
Transformate Fourier
• Obiectiv: descompunerea unui semnal complex intr-o suma de semnale simple– semnale simple: set de semnale sinusoidale
• pentru ca sunt ortogonale• nu isi schimba forma la trecerea printr-un sistem liniar
(se schimba amplitudinea si faza, dar semnalul ramane sinusoidal si de aceeasi frecventa)
– Mai multe tipuri de transformate Fourier pentru diferite tipuri de semnale:
Transformate Fourier
• Mai multe tipuri de transformate Fourier pentru diferite tipuri de semnale
Tip semnal Forma senalului Tip de transformata Fourier
Semnal aperiodic continuu
Transformata Fourier
Semnal periodic continuu
Serii Fourier
Semnal aperiodic discret
Transformata Fourier de timp discreta
Semnal periodic discret
Transformata Fourier discreta (DFT)
Transformata Fourier Discreta• se aplica numai semnalelor discrete periodice
– pentru ca are un numar finit de termeni– se poate calcula printr-un numar finit de pasi– semnalele digitale aperiodice pot fi “transformate” artificial in
semnale periodice– transformata Fourier discreta (DFT) transforma un set de N
esantioane de intrare (din domeniul timp) in 2 seturi de N/2+1 esantioane de iesire din domeniul frecventa
• un set de amplitudini pentru functii cosinus – partea reala – ReX[k], pentru functii ck[i] = cos (2πki/N) – cos() esantionat
• un set de amplitudin pentru functii sinus – partea imaginara– ImX[k], pentru functii Sk[i] = sin (2πki/N) – sin() esantionat
unde k=0 - N/2, iar i=0 – (N-1)
Sinteza unui semnal pe baza coeficientilor transformatei Fourier discrete:
• unde
sunt valorile normalizate ale coeficientilor din transformata Fourier discreta
Calcularea DFT• trei metode:
– didactica, dar foarte lenta– prin convolutie (clasica)– transformata Fourier rapida FFT
• Didactica:– folosind formula anterioara de sinteza, scriem N ecuatii cu N
necunoscute pentru cele N valori discrete ale lui x[i]• teoretic ar fi (N/2+1) + (N/2+1) = N+2 coeficienti de determinat, dar
se poate arata ca ImX[0]=0 si ImX[N/2]=0, asa ca raman N necunoscute ReX[k] si ImX[k]
– se rezolva setul de N ecuatii cu N necunoscute (ex. cu metoda eliminarii a lui Gauss)
– metoda prea lenta, nu se foloseste practic, dar arata teoretic de ce se pot determina coeficientii Fourier din N esantioane ale intrarii
Calcularea DFT prin convolutie
• se bazeaza pe ortogonalitatea functiilor elementare sinusoidale– daca un semnal de intrare x[i] contine o sinusoida de o anumita
frecventa atunci corelatia lui x[i] cu acea functie este diferita de zero (este amplitudinea acelei componente in x);
– daca semnalul nu contine acea componenta convolutia lui x[i] cu acea sinusoida este 0
• formula de calcul a coeficientilor:
Reprezentarea polara a transformatei Fourier discrete
• reprezentarea grafica a ReX[k] si ImX[k] nu este relevanta pentru ochiul uman– perechile sin si cos de aceeasi frecventa se transforma intr-o
functie cos dupa formula:
• A cos(x+θ)= C cos(x) + S sin (x)– pentru fiecare frecventa rezulta o magnitudine A (amplitudine) si
o faza θ, care se calculeaza cu:A[k] = ReX[k]2 + ImX[k]2
θ[k] = arctan(ImX[k]/ReX[k]))
ImX[k]
ReX[k]
θ[k]
A[k]
Reprezentarea frecventei in diagramele DFT (reprezentarea axei x)
• patru posibilitati de reprezentare a frecventei:– ca esantioane ale transformatei, de la 0 la N/2
• N este numarul de esantioane ale intrarii• de exemplu pentru N=128, se obtin 64 de esantioane ale transformatei• programatorii prefera aceasta metoda, desi nu este prea sugestiva privind
frecventele reale prezente in semnal– ca o fractie din frecventa de esantionare, cu interval de variatie (0-0,5)
• teorema lui Shannon limiteaza frecventa semnalului de intrare la jumatate din frecventa de esantionare
• trecerea din prima reprezentare in a doua se face prin divizare cu N– similar cu cazul 2 dar multiplicat cu 2π
• se obtine o variatie in radiani, intre 0 si π– ca o secventa de frecvente reale
• valorile din cazul 2 de reprezentare se inmultesc cu frecventa de esantionare• de exemplu daca frecventa de esantionare este 1000Hz atunci axa Ox variaza intre
0 si 500 Hz
Reprezentarea unui semnalin Domeniul timp si in Domeniul frecventa
Domeniul timp Domeniul frecventa
a. semnalul esantionat in timp
b. partea reala a transformatei (functii cos())
c. partea imaginara a transformatei (functii sin())
Reprezentare prin N/2
esantionane
Reprezentare prin fractii ale frecventei de esantionare
Transformata Fourier Rapida (FFT)
• observatii preliminarii:– o metoda de a calcula mult mai eficient DFT– timpul de calcul scade cu 2, 3 ordine de marime;– permite utilizarea transformatei Fourier ca metoda de analiza in aplicatii de
procesare a semnalelor on-line (in timp real)– complexitatea algoritmului de calcul al DFT prin convolutie este n2
;complexitatea FFT este n*lg n– explicarea bazelor matematice ale metodei FFT este mult mai complexa decat
forma algoritmului care rezulta– “FFT este pentru Procesarea digitala a semnalelor ca si un tranzistor pentru
circuitele electronice: o componenta de baza; • dar nu trebuie sa intelegi structura complexa a tranzistorului ca sa-l folosesti
cu succes; • doar un mic numar de specialisti inteleg cu adevarat cum functioneaza
tranzistorul (ca si FFT-ul) dar foarte multi il folosesc”
Metoda de calcul a FFT
• Secventa de calcul:– pasul 1: un semnal de N puncte din domeniul
timp se descompune in N semnale de cate un singur punct
– pasul 2: se calculeaza distributiile spectrale pentru cele N semnale de un punct
– pasul 3: cele N spectre obtinute se sintetizeaza intr-un singur spectru
Detalii privind calculul FFT
• Pasul 1: Decompozitia semnalului avand N puncte in domeniul timp– exemplu de descompunere pentru un semnal avand 16 puncte
Semnalul initial cu 16 puncte
2 semnale a cate 8 puncte
16 semnale a cate 1 punct
log2n pasi
Detalii privind calculul FFT• Pasul 2: descompunerea spectrala a semnalului de un punct
– banal: spectrul este egal cu valoarea punctului (demonstrat in teoria semnalelor)
– deci nu se calculeaza nimic, valorile spectrale sunt valorile punctelor din domeniul timp
• Pasul 3: sinteza spectrelor fiecarui punct pentru a obtine spectrul semnalului initial– sinteza se face in ordine inversa celei de descompunere:
• se combina cate 2 spectre de punct pentru a obtine spectrul pentru 2 puncte, apoi spectrele de 2 puncte cate 2 pentru a obtine spectre de cate 4 puncte s.a.m.d. pana la obtinerea spectrului pentru semnalul initial cu N puncte
Detalii privind calculul FFT
• Pasul 3(continuare):– exemplu de combinare a 2
spectre de 4 puncte pentru a obtine un spectru pentru 8 puncte
– operatia de baza: compozitia a 2 puncte in alte 2 puncte
Spectrul pentru 4 puncte impare
Spectrul pentru 4 puncte pare
Spectrul de frecventa pentru 8 puncte
2 puncte de intrare
2 puncte de iesire
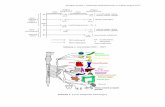
Unitate elementara de calcul de tip fluture (butterfly)
xS – reprezinta multiplicarea cu o sinusoida
Detalii privind calculul FFT
• Diagrama de executie a programului
Decompozitia semnalului de intrare
Antet
Antet
Calculul unei unitati butterfly
Semnal in domeniul timp
Distributia spectrala(semnal in domeniul frecventa)
log2n ori
pentru fiecare sub-DFT
pentru fiecare butterfly
Transformata Hilbert
Se ştie că un semnal armonic: x(t) = A cos(ω0t+φ) poate fi reprezentat ca suma a doi fazori:
Acelaşi semnal poate fi însă reprezentat şi ca partea reală a unei exponenţiale complexe:
Aplicând transformata Fourier semnalului xa(t) obţinem:
)AeRe(=(t)x Re=x(t) )+tj(a
00 ϕω
)-(eA=eeA F=(t)x F ojtjj
aooo ωωδφωφ
Se observă că transformata Fourier a semnalului xa(t) este nulă la frecvenţe negative. Un astfel de spectru este denumit spectru unilateral.
Transformata Fourier a semnalului real x(t) este:
)+(e2
A+)-(e
2
A=
2e+eA
F=x(t) F oj-
oj
)+t-j()+tj(
oo
oooo
ωωδωωδ φφφωφω
Se observă uşor că Xa(ω)=2X(ω)σ(ω), unde σ(ω) este treapta
unitate:
0<pt. 0
0>pt. 1=)(
ωω
ωσ
Se poate extinde reprezentarea complexă şi la semnale x(t) care nu sunt armonice, prin introducerea noţiunii de semnal analitic xa(t). Acesta este un semnal complex a cărui parte reală este chiar semnalul x(t) şi a cărui transformată Fourier este nulă la frecvenţe negative:
x(t): xa(t)= x(t) +j(t)
Se poate scrie în continuare:
Fxa(t) = Xa (ω) = X(ω)+ j(ω)= 2X(ω)σ(ω) şi din această relaţie rezultă: (ω)=(-j sgn ω )X(ω), unde sgn este funcţia:
0<pt. 1-
0>pt. 1 =)sgn(
ωω
ω
Părţile reală şi imaginară ale unui semnal analitic nu sunt independente. Transformatele Fourier ale lor au acelaşi modul, dar fazele diferă cu ±π/2 pentru frecvenţe pozitive şi negative. se numeşte Transformata Hilbert a lui x(t), astfel încât acum putem spune că un spectru unilateral are drept original o funcţie complexă, ale cărei părţi reală şi imaginară sunt legate prin Transformata Hilbert.Se poate scrie:
xa(t) = x(t)+j(t) =
unde
eA(t)=e(t)x+(t)x (t)j(t)j22 φφ~
x(t)
(t)xarctg=(t) ;)(tx+)x(t=A(t) 22
~~ φ
Am arătat mai înainte că: (ω)=(-j sgn ω)X(ω). Este uşor de arătat că originalul lui (-j sgn ω) este 1/πt (ţinînd cont de faptul că F(sgn t)=2/jωt şi folosind proprietăţile de simetrie ale Transformatei Fourier). Se poate scrie:
(t)=Hx(t)= ττ
τππ
d-t
1)x(
1=x(t)*
t
1
-∫∞
∞
Recapitulând, se poate spune că sunt 3 moduri diferite de a introduce Transformata Hilbert a unui semnal real x(t):
- ca parte imaginară a semnalului analitic asociat- utilizând produsul de convoluţie- modificând cu ± π/2 argumentul transformatei Fourier a
semnalului
Este important de subliniat că transformata Hilbert lasă semnalul original în acelaşi domeniu, timp sau frecvenţă.
Principalele proprietăţi ale transformatei Hilbert sunt enumerate mai jos:- liniaritatea:
Hax1(t)+bx2(t)= aHx1(t)+bHx2(t)
- ortogonalitatea: <x, > = 0=dsgn|)X(|X=(t)dtxx(t) 2
-
*
--
-j=)d(X)( ωωωωωω ∫∫∫∞
∞
∞
∞
∞
∞
~~
-HH(t)=-x(t)
Exemplu: Hcos ω0t =sin ω0t; Hsin ω0t =-cosω0t
Transformata Z
Semnale cu timp discret
• Un semnal cu timp discret se obţine prin memorarea valorii unui semnal cu timp continuu la anumite momente de timp,
echidistante. Valorile memorate se numesc eşantioane, iar procesul de memorare a acestur valori poartă numele de
discretizare a unui semnal cu timp continuu. Intervalul de timp intre 2 eşantioane se numeşte pas sau perioadă de eşantionare
şi în cele ce urmează se va nota cu T.
• De multe ori, semnalul obţinut se reprezintă ca în c) omiţând pe axa timp înmulţirea cu timpul de eşantionare T, astfel că
momentele de eşantionare kT apar ca fiind doar k Z. Un astfel de semnal se numeşte semnal discret.
Avantajele utilizarii sistemelor de procesare numerica fata de sistemele analogice
• Flexibilitate;• Eficienta economica;• Fiabilitate;• Diagnoza;• Integrare;• Adaptabilitate;• Stocarea si transmisia performanta a datelor;• Performante superioare.
Flexibilitate, Fiabilitatea si Integrarea
• Flexibilitatea. – Sistemul de prelucrare numeric se bazeaza pe un algoritm de
calcul, pe care-l efectueaza un sistem cu microprocesor sau microcontroller specializat;
– Algoritmul poate fi usor schimbat, reprogramat fara nici o modificare fizica a sistemului de calcul.
• Fiabilitate.– Depinde de partea hardware a sistemului care necesita
intretinere;
• Integrarea.– Sistemele digitale pot fi realizate intr-o capsula de circuit
integrat
Diagnoza, Adaptabilitatea, Stocarea si Transmisia datelor
• Diagnoza– Este necesara testarea atat in functionarea normala cat si in
situatii de avarie. Folosirea sistemelor digitale se preteaza mai bine decat cele analogice prin folosirea unor algoritmi care sa testeze si sa furnizeze informatii usor de interpretat despre starea sistemului, sau sa decida folosirea unor resurse hardware de rezerva;
• Adaptabilitatea– Un algoritm de procesare numerica poate fi folosit in mai
multe aplicatii prin ajustarea parametrilor;• Stocarea si transmisia datelor
– Datele numerice pot fi stocate mult mai rapid si cu o densitate mult mai mare pe unitatea de volum. De asemenea, semnalele numerice au o imunitate redusa la zgomot, atat in procesul de stocare cat si de transmisie.
Transferul de date
Termenul de date se refera la caractere alfabetice, numerice, sau cu destinaţie specială care sunt grupate în mod corespunzător în formă binară pentru a constitui cuvinte, mesaje, sau informaţii. Comunicaţiile de date se referă în primul rând la transferul de date de la un aparat dintr-o locaţie la un aparat aflat într-o altă locaţie. Două sau mai multe dispozitive care comunică unul cu celălalt formează un sistem şi dispozitivele se spune că sunt în reţea. Reţele pot fi cablate, wireless, sau o combinaţie a celor două. Transferul de date de la un dispozitiv la altul este măsurată ca și baud rate sau rată de biţi (bit rate). Rata baud (baud rate) indică numărul de simboluri transmise într-o unitate de timp, de obicei, pe secundă. Rata de biţi indică numărul de biţi transmiși pe secundă.
Rata baud şi rata de biţi sunt aceleaşi doar atunci când pentru fiecare simbol este alocat un singur bit. Dar simbolurile sunt de obicei exprimate ca o serie de biţi care formează cuvinte, fluxuri şi coduri. De exemplu codul Murray, care este utilizat pentru numere şi caractere alfanumerice, conţine cinci biţi pentru fiecare simbol. Informaţiile digitale sunt deseori transmise în secvenţe de date. O secvenţă de date este o colecţie de caractere pentru transmiterea unui mesaj complet și care poate fi înţeleasă de dispozitivul transmiţător şi de cel de recepţie. O secvenţă tipică de date este se arată în figură.
Transferul de date.
Când se utilizează secvenţele de date, rata de informaţie nu este la fel cu rata de biţi sau rata baud, deoarece el conţine în plus date de adrese, controale de eroare, precum şi informaţii de start și stop. Tipul de informaţii din secvenţe este reglementat de protocoalele şi standardele utilizate în aplicaţii speciale. Protocoale sunt configurate în cadrul unor modele de referinţă (de exemplu, modelele de referinţă ale The Institute of Electrical and Electronics Engineers [IEEE] 802 și Open Systems Interconnection [OSI]). Este de înţeles că atunci când sunt utilizate protocoale, rata de informaţii poate fi mult mai mică.
Transferul de date.
Transferul de date.
Teoria, protocoalele, precum şi implementarea sistemelor de comunicaţie digitale şi a reţelelor asociate care se bazează pe conexiuni fizice, cum ar ca fire sau cabluri optice sunt bine stabilite şi au fost folosite de mai mulţi ani. Cu toate acestea, în comparaţie cu tehnicile cablate, transmiterea de date wireless şi crearea de reţele de instrumente şi senzori este relativ nouă şi poate oferi multe facilităţi suplimentare.
Este suficient de spus că, în acest stadiu, componentele wireless din cele mai multe reţele wireless se comportă ca și omoloagele lor din reţelele cablate.
Astfel, principiile de funcţionare a reţelelor wireless și a reţelelor cablate au multe puncte comune, dar reţele wireless sunt în curs de dezvoltare ca o entitate separată în evoluţiile tehnologice şi în aplicaţii.În ambele tipuri de sisteme de comunicaţii, cablate şi wireless, datele pot fi transmise fie paralel sau serie, cu flux de informaţie sincron sau asincron, în formă de transport simplex, semi-duplex, sau full-duplex. Prin urmare, discuţiile prezentate pe aceste concepte sunt aplicabile atât sistemelor de comunicaţie cablate cât și reţelelor wireless.
Transmisia de date serială i paralelăș
Datele pot fi transmise de la un dispozitiv la altul în formă serială sau paralelă. În transmisiile de date seriale, fiecare bit al unui cod este trimis succesiv, după cum se arată în figură.
În consecinţă, transmiterea serială poate fi realizată de către o singură pereche de conductoare care conectează împreună un receptor şi un emiţător.
Transmisia de date serială i paralelăș
În transmisia paralelă a datelor, toţi biţii sau un număr de biţi a unui cod sunt transmiși simultan. Prin urmare, numărul de fire necesar este egal cu numărul de biţi de transmis plus firul de retur. De exemplu, pentru un cod de opt biţi este necesar ca cel puţin opt fire să se conecteze între emiţător şi receptor, astfel cum este ilustrat în figură.
Transmisia sincronă i asincronășTransmisia serială poate fi realizată în două forme: în mod asincron sau sincron. În transmisia asincronă, mesajele sunt transmise sub formă de blocuri. Această formă de transmitere poate conţine perioadele de repaus semnificative între blocuri şi este adesea utilizată în cazul în care nu este necesară o viteză mare de transmisie a datelor. Transmisia asincronă a datelor utilizează caractere de date care conţin informaţii cu privire la procesul de sincronizare, natura şi lungimea datelor, precum şi locaţiile primului şi ultimului bit din blocul de date, astfel încât receptorul să ştie caracteristicile informaţiei ce provine de la transmiţător. De vreme ce receptorul ştie bitul de start și bitul de stop al blocului, acesta poate fi trimis oricând şi cu orice rată. Fiecare bloc între emiţător şi receptor este sincronizat cu drepturi proprii prin utilizarea elementelor de start și stop. Lungimea fluxului de date si decalajul de timp dintre blocuri nu sunt de obicei fixe, dar sunt decise pe baza sincronizării. Fireşte, modul de transmisie asincron este mai lent decât modul de transmisie sincron din cauza adăugării elementelor de sincronizare.
Transmisia sincronă i asincronăș
Figura ilustrează un caracter binar tipic transmis în mod asincron.
Când caracterul este transmis, acesta este precedat de un bit de start (binary 0), urmat de un bit de paritate opţional şi unul sau mai mulţi biţi de stop. Bitul stop are de obicei valoarea binară 1.
Transmisia sincronă i asincronăș
În modul de transmisie asincron, receptorul detectează bitul de start prin sesizarea tranziţiei de la un marker la un spaţiu, apoi decodează următorii şapte biţi ca un caracter. În cazul în care trebuie transmise mai multe caractere, acest proces este repetat. Receptorul şi transmiţătorul au fiecare ceasul intern propriu, ambele fiind la aproximativ aceeaşi rată, dar aceste ceasuri nu sunt neapărat sincronizate. De asemenea, modul de transmitere asincron permite intervale de timp variabile între caractere transmise. Transmisia sincronă este o tehnică de transmisie bazată pe mesaj; acesta nu utilizează biţi de start și stop la fel ca transmisia asincron. Aceasta necesită un tact comun de ceas la cele două capete, de transmisie şi recepţie pentru a realiza sincronizarea. Utilizarea unui ceas comun ajută de asemenea la identificarea frecvenţei caracterelor.
Transmisia sincronă i asincronășReceptorul este capabil să recunoască un cod unic în biţii primiţi ca și flux de date de intrare. Acest cod permite receptorului să blocheze fluxul de biţi de intrare. Receptorul trebuie să fie setat la exact acelaşi ritm de ceas ca și transmiţătorul. Sincronizarea ceasului este cunoscută ca și sincronizare de biţi (bit synchrinization). Funcţionarea sincronă poate fi caracterizată după cum urmează: • Nu există biţi de start sau de stop pentru a sincroniza fiecare caracter. • Fiecare bit la emiţător şi la receptor trebuie să fie sincronizat la un ceas comun. • Datele sunt trimise în blocuri care constau din mai multe elemente, fără separare între ele. • Blocul în întregime este încadrat de codurile care indică începutul şi finalul. • Receptorul trebuie să cunoască codurile, lungimea de bloc, şi alte informaţii relevante şi de control. • Nu este sensibil la posibila denaturare a semnalelor transmise, deoarece cronometrarea se face într-un mod sincronizat. Cu transmisia sincronă, sincronizarea este tratată mai degrabă pe bază de mesaj decât pe bază de caracter. Odată sincronizate, nu se mai permite nici o pauză sau un interval între caractere. Acest lucru poate limita o comunicare eficientă între dispozitivele care nu au un flux continuu de informaţie sau dispozitive care nu au tampoane (buffere) pentru a stopa mesajele în cazul în care transmisia continuă nu poate fi menţinută.
Transmisia sincronă i asincronăș
Transmisiile sincrone şi asincrone sunt realizate cu dispozitive dedicate, cum ar fi universal synchronous-asynchronous receiver/transmitters (USARTs) și universal asynchronous receiver/transmitters (UARTs). USARTs şi UARTs sunt părţi importante în transmisia serială a datelor. Un USART este un dispozitiv care transformă biţii paraleli într-o un flux de date continuu serial, sau invers. Un USART poate funcţiona în formă sincronă sau asincronă. Un UART este un dispozitiv care se ocupă de comunicaţia serială asincronă. Un UART tipic este un dispozitiv programabil cu 40 de pini care transmite şi primeşte date în mod asincron fie în mod semi-duplex fie în mod full duplex. Un UART acceptă date paralele şi le converteşte în mod asincron pentru a le pregăti pentru o transmisie serială.
Transmisia de date simplex, half-duplex i full duplexș
Transmiterea de date între două dispozitive poate fi caracterizată ca: simplex, semi-duplex sau duplex complet, după cum se arată în figură.
Operarea simplex indică faptul că transmisia poate avea loc într-o singură direcţie de la un aparat la altul. În acest mod, unul dintre dispozitivele poate transmite, dar nu poate recepţiona, sau recepţionează dar nu transmite. Operarea half-duplex se referă la o transmisie în orice direcţie, dar aceasta poate avea loc într-o singură direcţie la un moment dat. Operarea full-duplex indică faptul că operaţiunea de transport are loc în ambele direcţii simultan. În reţelele unde sunt implicate în comunicare multe dispozitive, transmisia utilizează mai multe canale. Un canal este definit ca o singură cale pe o linie prin care circulă semnalele. Liniile sunt definite ca și componentele şi părţile care se extind între terminalele dispozitivelor de comunicare.
Transmisia de date simplex, half-duplex i full duplexș
Un exemplu de operare simplex este un sistem de paging. În paging, mesaje sunt primite, dar nu neapărat confirmate. Un exemplu de operare semi-duplex este un walkie-talkie. În walkie-talkie, operatorul apasă un buton pentru a vorbi şi eliberează butonul pentru a asculta. Ambii operatori nu pot să comunice în acelaşi timp. Un sistem full-duplex oferă simultan, dar separat canale prin tehnici cum ar fi duplexarea divizării de frecvenţă (FDD) sau duplexarea divizării de timp (TDD). FDD utilizează canale de frecvenţă diferite şi TDD folosește intervale de timp adiacente pe un singur canal.
Transmisia de date simplex, half-duplex i full duplexș
Transmisia de date wireless
Dispozitivele pot comunica prin conexiuni wireless sau cablate formând reţele locale de zonă (LAN). Componentele wireless ale celor mai multe reţele locale se comportă la fel ca și omoloagele lor cablate, dar ele utilizează spaţiul ca și mediu de transmisie. Principiile operaţionale ale reţelelor cablate și wireless sunt asemănătoare: este necesar să se anexeze o interfaţă de reţea pentru dispozitivele care transmit respectiv recepţionează. În cazul reţelelor wireless, interfaţa este mai degrabă un transciever de radiofrecvenţă (RF) decât cabluri. În multe cazuri, sistemele cablate şi sistemele wireless sunt folosite împreună, într-o formă mix-and-match. În cazul interfaţării sistemelor wireless cu sisteme cablate, sunt utilizate dispozitivele numite puncte de acces (access point) pentru a realiza această conexiune. Acest lucru permite transferul traficului de date între componentele cablate şi wireless.
În sistemele de comunicaţii wireless, frecvenţele utilizate pentru transmiterea datelor afectează cantitatea de date şi de viteza la care datele pot fi transmise. Tăria sau nivelul de putere a semnalului de transmisie determină distanţa la care datele pot fi trimise şi primite, fără erori şi de corupţie. În general, principiul care reglementează transmisiile wireless stipulează că o frecvenţă mai mică de canal poate transporta mai puţine date, mai lent, dar pe distanţe mai lungi. Pe de altă parte, frecvenţele mai mari pot transporta mai multe date, la rate mai rapide, dar distanţa de transport eficient devine mai scurtă. Sistemele moderne de comunicaţii wireless utilizează în mare măsură partea de mijloc a spectrului electromagnetic. Partea de mijloc a spectrului electromagnetic este împărţită în mai multe game de frecvenţe, sau benzi, pentru scopuri de comunicare. Aceste benzi de frecvenţă sunt:
•spectrul de frecvenţe radio (10 kHz până la 1 GHz);•spectrul de frecvenţe cu microunde (1 GHz la 500 GHz);•frecvenţa vizibilă și în infraroşu (500 GHz până la 1 THz).
Transmisia de date wireless
Eficienta economica. Performante superioare
• Eficienta economica– Pentru modificarea comportamentului unui amplificator
numeric se modifica programul (o parte din algoritmul de calcul) fara modificari fizice ale sistemului.
– In cazul unui amplificator analogic cu tranzistoare, pentru modificarea caracteristicilor trebuie modificate diferite componente (R, C) ceea ce implica cheltuieli materiale, experimente, teste etc
• Performante superioare– Exista numeroase tipuri de procesari a datelor care nu pot fi
realizate in sisteme analogice (filtre de ordin superior);