t. Sorohan

I. N. Constantinescu

PRACTICA MODELRII I ANALIZEI CU ELEMENTE FINITE

PREFALucrurile sunt numere Pitagora Metoda elementelor finite (MEF) este departe de a fi perfect, dar este cea mai bun dintre metodele disponibile n prezent pentru o mare varietate de tipuri de calcule, n toate domeniile activitilor inginereti. Metoda i programele bazate pe ea, au devenit componente fundamentale ale sistemelor de proiectare asistat de calculator (CAD) i sunt indispensabile n toate situaiile n care se cere competitivitate unei activiti inginerti. Cartea pe care o avei n fa nu este un curs de elemente finite. Ea se adreseaz unor utilizatori care au cunotine n MEF, cel puin la un nivel introductiv. De asemenea, autorii au presupus c cititorii crii au o minim experien n modelarea unei structuri simple i n utilizarea unui program cu elemente finite. Ideea fundamental a lucrrii este c pentru analiaza cu elemente finite (FEA) demersul principal este elaborarea unui model de calcul corect, adecvat i eficace, ceea ce reprezint ntr-o mare msur o provocare i o art, procesul modelrii avnd un mare grad de arbitrar, prin care trebuie satisfcute cerine multiple i contradictorii. Capitolele, sau subiectele, abordate n carte, sunt foarte variate, viznd aspecte teoretice, dar mai ales practice, ale modelrii i analizei cu elemente finite, cu referiri i exemplificri la structuri mecanice ct mai diverse. Redactarea materialului s-a fcut astfel nct fiecare cititor s poat parcurge fr dificultate doar subiectele care l intereseaz. Din acest motiv capitolele sunt inegale ca ntidere, unele avnd doar cteva pagini iar altele cteva zeci de pagini. Aplicaiile i exemplele incluse n carte au fost tratate cu programe consacrate, cunoscute i comercializate pe piaa soft, sau programe proprii. Programele consacrate au fost accesate n cadrul catedrei de Rezistena materialelor a Universitii Politehnica din Bucureti. Autorii nu au menionat numele programelor utilizate pentru a nu face reclam sau a nu aduce critici acesora, adic pentru a nu implica n nici un fel firmele care produc i (sau) comercializeaz programele respective. n carte au fost nserate numeroase aplicaii i exemple pentru a enuna, ilustra i motiva diverse aspecte ale modelrii i analizei cu elemente finite. Unele aplicaii sunt simple, altele se refer la structuri industriale. Rezultatele analizelor au fost prezentate sub cele mai diversificate forme (tabele, grafice, diagrame) cu scopul ca ele s permit o nelegere facil i formularea unor concluzii ct mai clare i mai convingtoare. Aspectele practice ale modelrii i analizei cu elemente nu au fost nici pe departe epuizate n lucrare. De asemenea, sunt multe aspecte ale tematicii abordate, pe care autorii le-au semnalat, dar crora nu au putut s le gseasc soluii satisfctoare. Fr idei preconcepute i cu bun credin, autorii s-au strduit ca n cartea de fa s evidenieze unele aspecte, mai puin sau deloc abordate n lucrrile de prezentare a MEF i FEA, neclare sau controversate, cu scopul de a atrage atenia utilizatorilor asupra lor i astfel s-i ndemne la pruden i discernmnt n munca lor. n ce msur cartea de fa va reui s realizeze acest deziderat al autorilor, vor hotr cititorii.

Bucureti, iunie 2003

Cuprins

1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32.

Sinteza i analiza structurilor mecanice. Locul analizei cu elemente finite n realizarea unui produs Conceptele de baz ale metodei elementelor finite Elemente de teoria elasticitii ... Scurt prezentare a metodei elementelor finite - principiile fundamentale . Avantajele, dezavantajele i limitele metodei elementelor finite ... Discretizarea - demersul fundamental al modelrii cu elemente finite Modelul de calcul i importana sa n ingineria asistat . Verificarea modelelor de calcul cu elemente finite .. Postprocesarea analizelor cu elemente finite .. Surse de erori n modelarea cu elemente finite ... Eficiena modelelor cu elemente finite .. Submodelare i substructurare .. Proceduri speciale n programele cu elemente finite .. Capcane ale practicii analizei cu elemente finite . Modele parametrice pentru analiza cu elemente finite .. Modelarea pentru analize locale Modele diferite pentru aceeai structur .. Particulariti ale modelrii i analizei cu elemente finite a structurilor industriale Exemple de structuri modelate i analizate cu elemente finite .... Interfaa CAD - elemente finite ... Aspecte fundamentale ale modelrii i analizei problemelor dinamice ... Structuri axial simetrice solicitate nesimetric ... Unele aspecte ale modelrii i analizei structurilor neliniare . Aspecte fundamentale ale modelrii i analizei problemelor de contact . Modelarea i analiza structurilor la stabilitate .. Propagarea i transmisia cldurii n modelarea i analiza cu elemente finite ........................................ Aspecte practice ale optimizrii structurilor .. Modelarea i analiza reelelor de conducte .. Modelarea n biomecanica sistemului osteo-articular uman . Simulri cu elemente finite ..... Elemente finite pentru materiale compozite ........................................................................ Modelarea i calculul cu elemente finite la solicitri variabile oboseal..........

1 3 10 19 49 52 57 62 67 77 90 95 100 130 138 143 153 159 163 173 180 209 220 232 254 269 281 287 291 295 300 307

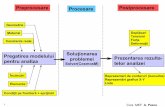
1.SINTEZA I ANALIZA STRUCTURILOR MECANICE. LOCUL ANALIZEI CU ELEMENTE FINITE N REALIZAREA UNUI PRODUSProiectarea este o activitate de creaie, cu implicaii multidisciplinare. Pentru rezolvarea unei probleme, proiectantul trebuie s primeasc informaii care s-i permit s formuleze problema dat n termeni numerici. Dac tema pe care a primit-o conine condiii calitative, la care nu s-au asociat i termeni cantitativi, este de ateptat ca soluia s fie nesatisfctoare, cel puin din unele puncte de vedere. Scopul primordial al proiectrii este de a obine cel mai bun sistem posibil pentru un ansamblu de cerine impuse. Pentru aceasta se concepe un sistem candidat i se studiaz cum se comport acesta. n inginerie n general, precum i n construcia unei maini, a unui utilaj sau a unei instalaii, o component de baz este structura de rezisten, care reprezint un ansamblu mecanic cu o funcionalitate riguros definit, ca de exemplu: preluarea diverselor sarcini, asigurarea unei anumite poziii relative ntre subansamble, posibilitatea efecturii unor micri relative ntre unele componenete, asigurarea unei stabiliti statice i dinamice, garantarea unei rigididiti impuse etc. n limbajul ingineresc obinuit structura de rezisten se numete mai simplu: structur. Calculele de rezisten, de stabilitate, de durabilitate, dinamice etc au n vedere structura de rezisten n ansamblu, componentele acesteia, precum i alte elemente, componente sau subansamble ale mainii, utilajului sau instalaiei care se proiecteaz. Aceste calcule constitue o componenet important a proiectrii dar ele pot fi duse la bun sfrit numai dup ce alte aspecte, de principiu sau de detaliu, au fost clarificate. Este cazul cerinelor beneficiarului, a costurilor impuse, a termenelor acordate, a materialelor disponibile, a tehnologiilor accesibile, a volumului produciei, a durabilitii cerute produsului, a exigenelor ecologice etc. Totdeauna calculele inginereti trebuie s aib n vedere satisfacerea optim a funciilor i cerinelor fundamentale ale proiectrii, ceea ce conduce la concluzia c disocierea procesului de calcul de cel de proiectare implic riscul unor consecine nefavorabile, care pot fi grave, greu de anticipat. O prezentare concis i sugestiv a acestor corelaii multiple se face n schema din figura 1.1.

Figura 1.1

1

Sinteza i proiectarea structurii de rezisten trebuie realizate n aa fel nct aceasta (adic structura) s fie sigur pentru valori clare ale parametrilor funcionali riguros definii, n condiiile ndeplinirii unor cerine severe i adesea contradictorii privind costurile, aspectul estetic, termenele de execuie, dimensiunile de gabarit, fiabilitatea etc. ndeplinirea acestor cerine duce la considerarea unor restricii pe care trebuie s le satisfac calculele, cele mai des ntnlite fiind: valorile maxime ale tensiunilor, deplasrilor i/sau deformaiilor, coeficientul de siguran la flambaj, la rupere sau la oboseal, minimum de sensibilitate la imperfeciuni de execuie, de montaj sau de exploatare, frecvenele modurilor fundamentale de vibraii, viteza de deformare n curgerea plastic staionar, durata de via, greutatea, volumul, rigiditatea la diverse solicitri, momentele de inerie, stabilitatea static i dinamic, comportarea la solicitri dinamice. Mai pot fi avute n vedere diferitele moduri de rupere, suprasarcinile la transport, la montaj sau n exploatare, precum i prevederile diverselor legi, standarde, norme etc. n prezent, marea majoritate a calculelor inginereti cerute pentru sinteza, proiectarea i analiza unui produs se pot face cu metoda elementelor finite (MEF). n condiiile proiectrii asistate de calculator (CAD) i a fabricaiei asistate de calculator (CAM), analiza cu elemente finite (FEA) devine o component a unui proces unitar integrat, aa cum se poate vedea n figura 1.2. Trebuie remarcat faptul c n succesiunea CAD FEA CAM exist un proces iterativ de proiectare calcul - execuie. n acest proces se realizez succcesiv operii de sintez i de analiz ale prototipului i ale modelului pentru calculul cu elemente finite (fig. 1.2). La fiecare iteraie a procesului se aduc mbuntiri ale prototipului i (sau) ale modelului de calcul, pn cnd se ating performanele dorite.

Figura 1.2 Analiza cu elemente finite (FEA) a modelului unei structuri de rezisten este un calcul numeric de verificare, adic pentru o anumit geometrie definit dimensional, pentru o ncrcare dat i condiii de rezemare bine precizate se obin valorile deplasrilor, tensiunilor, reaciunilor n reazeme, frecvenelor vibraiilor proprii etc. Nu este ns evident (n cazul general) cum trebuie modificat structura pentru ca aceasta s rspund ct mai bine ansamblului cerinelor impuse. Deci nu se poate concepe o tehnic general de optimizare automat, care s rezolve orice problem, de orice natur. Ce se poate face, este elaborarea unei metodologii de proiectare optim. Programele MEF actuale au implementate proceduri speciale de optimizare care permit determinarea prin calcul automat a valorilor optime ale unor parametri de proiectare astfel nct s fie satisfcute un set de condiii impuse unei funcii obiectiv, definit de utilizator.

2

2.CONCEPTELE DE BAZ ALE METODEI ELEMENTELOR FINITESimplitatea conceptelor de baz ale metodei elementelor finite (MEF) este unul dintre avantajele importanate ale acesteia. Importana nsuirii i a nelegerii corecte a acestora rezult din faptul c aceste concepte includ anumite ipoteze, simplificri i generalizri a cror ignorare poate duce la erori grave n modelarea i analiza cu elemente finite (FEA). Se prezint, n continuare, cele mai importante dintre conceptele de baz ale MEF.

StructuraPentru a avea o eficien ct mai ridicat, n FEA se utilizeaz un concept de structur mai general i mai simplu dect n mod obinuit. Uzual n FEA prin structur (de rezisten) se nelege un ansamblu de bare, plci, nveliuri i volume (solide). De exemplu, o structur poate fi batiul unui strung paralel, trenul de aterizare al unui avion, braul unei balane, carcasa unui reactor nuclear, corpul unui submarin, o reea de conducte etc. Definit astfel, noiunea de structur implic acceptarea ipotezei seciunii plane, a lui Bernoulli, pentru bare i a ipotezei normalei rectilinii, a lui Kirchhoff, pentru plci i nveliuri. Acceptarea acestor ipoteze face posibil, n MEF i FEA pentru bare i plci - nlocuirea forelor exterioare reale prin rezultantele interne eforturile N, T, M cu care sunt static echivalente, ceea ce nu este permis n teoria elasticitii. n analiza structurilor se poate deci introduce conceptul de for concentrat, fr ca prin aceasta s se produc cmpuri de tensiuni, deformaii i (sau) deplasri cu singulariti, aa cum se ntmpl n teoria elasticitii, cnd aplicarea unei fore concentrate ntr-un punct al semispaiului elastic (problema lui Boussinesq) duce la producerea unor tensiuni i deplasri infinite n punctul respectiv. De asemenea, conceptul sau noiunea de structur, definit ca mai sus permite stabilirea teoremelor deplasrii unitate i a forei unitate ale lui Maxwell precum i a teoremelor lui Castigliano, care au un neles clar n rezistena materialelor i n teoria structurilor, dar nu i n teoria elasticitii.

Modelul de calculPentru a putea efectua o analiz cu elemente finite a unei structuri, demersul hotrtor care trebuie ntreprins este elaborarea modelului de calcul al structurii respective. Toate aspectele privind acest proces se prezint n detaliu ntr-un paragraf separat, datorit importanei subiectului. Modelele MEF sunt modele matematice aproximative ale structurii care urmeaz s fie analizat. Pentru trecerea de la structura real la modelul ei de calcul nu exist algoritmi i metode generale care s asigure elaborarea unui model unic, care s aproximeze, cu o eroare prestabilit, cunoscut, structura care urmeaz s se aproximeze. n general este posibil ca pentru o structur s se elaboreze mai multe modele, toate corecte dar cu performane diferite. Modelul pentru calculul de rezisten al unei structuri se elaboreaz pe baza intuiiei, imaginaiei i experienei anterioare a celui care face modelarea. Modelul trebuie s sintetizeze eficient toate informaiile disponibile referitoare la structura respectiv. Elaborarea unui model de calcul corect i eficient depinde de anumii factori i trebuie s ndeplineasc anumite condiii. Toate aceste aspecte se prezint detaliat n cadrul capitolului 7 .

3

DiscretizareaModelul de calcul al structurii care urmeaz s fie supus analizei cu elemente finite, n cazul general, este format din linii, care sunt axele barelor structurii, din suprafee plane i curbe, care sunt suprafeele mediane ale plcilor componenete ale structurii i volume, care sunt corpurile masive ale structurii. n aceast etap a elaborrii, modelulul este un continuu, cu o infinitate de puncte, ca i structura dat. Discretizarea este demersul fundamental cerut de MEF i const n trecerea de la structura continu (cu o infinitate de puncte) la un model discret, cu un numr finit de puncte (noduri). Aceast operaie se face acoperind modelul cu o reea de dicretizare i se justific prin aceea c din punct de vedere practic, ingineresc, sunt suficiente informaiile privind structura (ca de exemplu, cunoaterea valorilor deplasrilor i ale tensiunilor) ntr-un numr oarecare de puncte ale modelului, numrul acestora putnd fi orict de mare. Metoda elementelor finite, n mod obinuit, definete necunoscutele (deplasri sau eforturi) n punctele modelului i calculeaz valorile lor n aceste puncte. n aceste condiii, rezult c dicretizarea trebuie fcut astfel nct s se defineasc un numr suficient de mare de puncte n zonele de interes, pentru ca aproximarea geometriei structurii, a condiiilor de rezemare i a condiiilor de ncrcare s fie satisfctoare pentru scopul urmrit de FEA. Din cele menionate rezult importana deosebit a modului cum se face dicretizarea modelului, motiv pentru care toate detaliile procesului de discretizare se prezint cadrul unui capitol special, care este capitolul 6.

NodulPunctele definite prin reeua de dicretizare se numesc noduri. n noduri se definesc necunoscutele nodale primare, ale cror valori sunt rezultatele FEA. Necunoscutele asociate nodurilor pot fi deplasrile, caz n care MEF se numete model deplasare, sau eforturile, cnd MEF se numete model echilibru. Relativ rar se folosete i modelul mixt. Pentru modelul deplasare se admite c forma deformat a structurii, ca urmare a unei solicitri oarecare, este definit de deplasrile tuturor nodurilor n raport cu reeaua nodurilor nainte de deformare, fiecare nod putnd avea maximum ase componente ale deplasrii, denumite deplasri nodale, n raport cu un reper global (la care este raportat structura n ansamblu): trei componente u, v, w ale deplasrii liniare i trei rotiri x, y, z. Componentelor nenule ale deplasrilor pe care le poate avea un nod al modelului structurii n procesul de deformaie li se asociaz un versor denumit grad de libertate geometric DOF al nodului, care are valoarea DOF=0, dac pe direcia respectiv componenta deplasrii este nul sau cunoscut i valoarea DOF=1, dac deplasarea este necunoscut. Se pot defini gradele de libertate geometric ale structurii n totalitate. Rezult c numrul total al necunoscutelor care trebuie determinate prin calcul este egal cu numrul gradelor de libertate geometric crora le sunt ataate necunoscute (care au DOF=1), pentru toate nodurile modelului structurii. Unele din gradele de libertate ale modelului trebuie eliminate deoarece unele noduri sunt legate, reprezentnd reazeme i deci deplasrile lor sunt nule sau au valori cunoscute, impuse i nu mai trebuie calculate.

Elementul finitProcesul de discretizare are drept urmare mprirea modelului structurii ntr-un numr oarecare de fragmente sau elemente, aa cum, de exemplu, zidul unei cldiri poate fi privit ca fiind format din crmizile utilizate la construcia sa. De exemplu, recipientul din figura 2.1, executat din table asamblate prin sudur, poate fi descompus sau discretizat ntr-un numr de elemente patrulatere i triunghiulare - denumite elemente finite - ca n figura 2.2. Elementele finite se leag ntre ele prin nodurile comune, care sunt vrfurile patrulaterelor sau triunghiurilor (sunt i tipuri de elemente care au noduri i pe laturi). Un element finit poate fi privit ca o pies de sine stttoare, interacionnd cu celelalte elemente numai n noduri. Studiul structurii reale se nlocuiete cu studiul ansamblului de elemente finite obinut

4

prin discretizare, care devine astfel o idealizare a structurii originare i este un model de calcul al structurii date. Pentru ca rezultatele analizei s fie ct mai precise trebuie ca procesul de idealizare al structurii date s fie ct mai performant, ceea ce implic respectarea unor regului i exigene privind discretizarea, elaborarea modelului de calcul i - printre altele - utilizarea unor elemente finite adecvate. n principiu, dimensiunile elementelor finite pot fi orict de mici, dar trebuie totdeauna s fie finite, adic nu poate fi fcut o trecere la limit prin care dimensiunile acestora s tind spre zero.

Figura 2.1

Figura 2.2

Din nefericire, nu se poate concepe un element finit general, care s aib o utilitate universal. Pentru a putea fi implementat ntr-un program MEF i utilizat pentru un model de calcul, elementul finit trebuie n prealabil proiectat n toate detaliile, adic trebuie definit din punct de vedere geometric, fizic, matematic etc. Privit din punct de vedere informaional, un element finit este un dispozitiv - sau un model care trebuie s poat prelucra ct mai precis un volum ct mai mare de informaii, pentru un set de condiii impuse. Aceasta presupune ca elementul de o anumit form geometric, de exemplu triunghiular, s aib un numr ct mai mare de noduri, fiecare nod s aib un numr ct mai mare de grade de libertate geometric, iar funciile de interpolare s fie ct mai complexe, adic s aib un numr ct mai mare de parametri. Desigur c meniunile anterioare sunt de principiu, deoarece cu ct crete complexitatea elementului finit cresc i dificultile de calcul, astfel nct pentru fiecare situaie concret n parte se caut o soluie de compromis cnd se concepe un element finit de un anumit tip. O consecin nefast a acestei situaii este c programele MEF au biblioteci cu un numr relativ mare de tipuri de elemete finite, pentru a satisface un numr ct mai mare de cerine, ct mai diverse. Ideea de baz a MEF este c, pentru un element de un tip oarecare, trebuie fcut ipoteza c deplasrile din interiorul elementului variaz dup o lege cunoscut, aleas apriori, determinat de o funcie de interpolare. Consecina acestui demers este c, local, acolo unde se va afla plasat elementul finit, n urma procesului de discretizare, acesta va aproxima starea de deplasri a structurii prin legea de interpolare implementat n elementul respectiv.

Figura 2.3 Funciile de interpolare au frecvent forma unor polinoame. Alegerea gradului polinomului i determinarea valorilor coeficienilor acestora trebuie s asigure o ct mai bun aproximare a soluiei

5

exacte necunoscute a problemei date. n figura 3 se prezint schematic modul n care polinoamele de gradul zero, unu i doi respectiv cu unu, doi i trei termeni - pot aproxima o stare de deplasri oarecare. Elementele care au aceleai tipuri de funcii (de obicei polinoame), att pentru definirea geometriei elementului (de exemplu, pentru laturile sale), ct i pentru definirea deplasrilor n interiorul su (funcia de interpolare), se numesc elemente izoparametrice i sunt cele mai eficiente i folosite elemente finite n practica MEF. Elementele finite se pot clasifica dup diverse criterii, dintre care cele mai importante sunt: Tipul de analiz. Pe o reea de discretizare se pot defini elemente finite care au incluse diverse proceduri matematice destinate unor analize diverse, ca, de exemplu: liniar elastic, neliniar, transfer de cldur, mecanica fluidelor, electro magnetism, electro magnetism de nalt frcven etc. Rolul funcional. Elementele finite utilizate pentru modelarea unei structuri trebuie s poat asigura ct mai bine rolul funcional al structurii date, adic, de exemplu, o grind cu zbrele trebuie modelat cu elemente de tip bar, un capac din tabl subire trebuie modelat prin elemente de tip plac, o fundaie prin elemente de tip crmid etc. Din aceste considerente elementele sunt de tip punct (element de mas sau de tip arc), de tip linie (elemente de bare drepte sau curbe, n plan sau n spaiu) de tip suprafa (elemente de plci plane sau curbe, groase sau subiri, n plan sau n spaiu, elemente axial simetrice, de membran etc) sau de tip volum (elemente spaiale, - 3D pentru structuri solide, compozite, cu numr variabil de noduri, pentru fluide, piezoelectrice, magnetice etc). Fiecare din categoriile de elemente enumerate au mai multe variante, numrul acestora putnd ajunge la cteva zeci. De asemenea, categoriile prezentate includ i elemente cu rol funcional special, ca de exemplu: rigid, de contact, de frecare, de legtur, definit prin matricea de rigiditate etc. Forma geometric. Elementele finite au, n general, forme simple ca, de exemplu, linie dreapt sau arc de cerc, triunghi, patrulater oarecare, tetraedru, hexaedru etc. De asemenea, unele caracteristici geometrice pot fi constante sau variabile, ca seciunile barelor sau grosimile plcilor. Numrul nodurilor. Pentru unele dintre elemente, o form geometric dat, de exemplu un triunghi, poate avea mai multe variante n ceea ce privete numrul de noduri, deoarece n afara nodurilor din vrfuri mai pot exista noduri i pe laturi i (sau) n interior. De asemenea se pot utiliza noduri i n interiorul elementului, pentru rezultate. Se utilizeaz i elemente cu numr variabil de noduri, ca, de exemplu, pentru plci groase elementul poate avea ntre 8 i 48 de noduri. Numrul gradelor de libertate ale fiecrui nod. Nodurile elementelor au ataate, implicit, unele DOF din cele ase posibile, deci se poate opera i cu numrul total de DOF pentru un element, care este numrul nodurilor nmulit cu numrul DOF pe nod. Gradul polinomului de interpolare. Fiecare element finit are implementate polinoame de interpolare de un anumit grad, ncepnd cu gradul nti. Cu ct gradul polinoamelor este mai ridicat cu att crete cantitatea de informaii cu care elementul opereaz i deci el este, n general, mai performant. Caracteristicile materialului. n practica FEA, materialul elementului finit poate fi omogen i izotrop sau cu o anizotropie de un anumit tip. De asemenea, constantele elastice i fizice ale materialului pot fi dependente de temperatur sau solicitare. Trebuie fcut precizarea c descrierea de mai sus a elementelor finite nu este exhaustiv, ci c ea doar semnaleaz unele aspecte importante din practica MEF. n concluzie, se menioneaz c fiecare tip de element finit este un ansamblu de condiii i ipoteze i el trebuie privit ca un ntreg i folosit ca atare, numai dup ce s-a studiat temeinic documentaia care l nsoete. De exemplu, din parametrii care definesc elementul rezult comportarea sa la solicitare, tipul strii de tensiuni, interaciunea sa cu celelalte elemente etc. Programele MEF care se folosesc n practica FEA au biblioteci cu un numr impresionant de tipuri de elemente finite, la care se adaug periodic elemente noi. Pentru a ilustra dinamica dezvoltrii MEF, se citeaz articolul [1], n care nc din anul 1984 se identificaser 88 de variante ale elementelor finite de plac.

6

Aproximarea i interpolarea Un model matematic pentru analiza unei structuri de rezisten implic determinarea unui numr de variabile i funcii u*( ) reprezentnd deplasri, deformaii, tensiuni etc, fiind funcii de coordonate (x,y,z), definite n punctele domeniului pe care este definit structura. Dac soluia exact u*() nu se cunoate i u() este o aproximare a acesteia, funcia eroare e() este e() = u() - u*(). ( 2.1)

Pentru constituirea unei soluii aproximative este suficient s se descrie o expresie care s conin n parametrii de aproximare ai u() = u(, a1, a2, ,an) i s se determine aceti parametri pe baza relaiei (2.1) i a unui criteriu de convergen adecvat. n MEF aproximarea este nodal i are forma u1 u2 u( ) = [ N1() N2() Nn () ] . = [N]T{un}, . un

n care: ui sunt parametrii nodali ai aproximrii i au o semnificaie fizic concret (deplasri nodale, temperaturi nodale etc); Ni() - funcii de interpolare sau de aproximare, care de regul au forme polinomiale. Soluiile aproximative u() pot fi construite pe ntreg domeniul V de definiie a structurii sau pe subdomenii elementare Ve ale elementelelor finite - ceea ce nseamn c Ve V . n MEF aproximaia nodal se face pe subdomenii Ve, care sunt de fapt elementele finite, valorile funciilor aproximative ui( ) = u*(xi) fiind variabilele nodale ale problemei iar xi, coordonatele nodurilor. n mecanica structurilor se poate construi o funcional care este energia potenial total a structurii. Impunnd acestei funcionale condiia de staionaritate

= W = 0,se obine ecuaia caracteristic W(u) =

V

R(u)wdV

=

V

w(L(u)

f v ) dV = 0

n care: L(u) este soluia exact a problemei; fV soluia aproximativ; R(u) = (L(u) - fV) - funcia reziduu; w - funcii pondere, denumite i funcii de corecie. Precizia soluiei u depinde de alegerea funciilor de pondere w, care au uzual forma

w = i i ,i=1

k

n care: i sunt un set de funcii liniar independente; i - coeficieni numerici arbitrari. Presupunnd c soluiile aproximative u satisfac condiiile de margine ale structurii, eroarea de aproximare reprezentat de rezidul R(u) este ponderat (distribuit) prin multiplicare cu funciile de pondere w, pe ntreg domeniul V. Dac funcionala structurii este (u) aceasta se poate aproxima prin procesul de discretizare, devenind (u) = [u (a1, a2, ,an)],

7

sau

a1 + a2 + .... + an. a1 a2 an Se obine sistemul de ecuaii = 0, i =1, 2, ..., n , ai prin rezolvarea cruia se determin parametrii ai ai aproximrii i se rezolv problema MEF. = Tabelul 2.1 Tipul funciilor Din interiorul elementului Deplasri continue Tensiuni continue aflate n echlibru Tensiuni continue aflate n echlibru Deplasri continue Deplasri continue Continuitatea Eforturilor i Funcii ale deplasrilor Deplasri continue Tensiuni continue aflate n echlibru Condiiile impuse n lungul frontierelor dintre elemente Compatibilitatea deplasrilor Echilibrul eforturilor de pe frontiere Necunoscutele din sistemul final de ecuaii Deplasrile nodale

Metoda elementelor finite

Principiul varaiional

Model deplasare, cu elemente conforme

Model echilibru H I B R I D M I X T Metoda generalizat a deplasrilor Metoda generalizat a eforturilor Metoda hibrid a deplasrilor (1) Metoda hibrid a deplasrilor (2) Principiul lui Reissner Metoda hibrid a eforturilor

Minimum energiei poteniale Minimum energiei complementare Energia complementar modificat Energia potenial modificat Energia potenial modificat Metoda lui Reissner modificat de Herrmann Energia potenial modificat Energia complementar modificat

a. Deplasri generalizate b. Eforturi parametrice Compatibilitatea Deplasrile deplasrilor nodale Compatibilitatea deplasrilor Echilibrul eforturilor de pe frontiere Combinarea eforturilor i deplasrilor de pe frontiere Multiplicatorii Lagrange pentru eforturi Multiplicatorii Lagrange pentru Deplasri Deplasrile nodale Deplasrile nodale i eforturile de pe Frontiere Combinarea eforturilor i deplasrilor Deplasrile nodale i Multiplicatorii Lagrange Deplasrile nodale i Multiplicatorii Lagrange

Varaiante conceptuale de formulare a MEFCnd a aprut MEF, prin anii 60, fundamentarea matematic era foarte sumar, utilizarea metodei fcndu-se mai mult intuitiv. Ulterior, pe msura clarificrii conceptelor de baz, MEF a fost formulat

8

n diverse variante, dintre care cele mai cunoscute au fost trecute n revist n lucrarea [2], n anul 1969 i n lucrarea [1], n 1984, din care se reproduce Tabelul 2.1. Se menioneaz faptul c i n prezent se utilizeaz mai multe formulri ale MEF, fiecare variant avnd avantajele, dezavantajele, susuintorii i utilizatorii ei. Dar aceste aspecte aparin mai ales speculaiilor matematice i nu fac obiectul prezentei lucrri. n programele MEF actuale se folosete mai ales modelul deplasare, pentru care neconoscutele sunt deplasrile nodale.

Bibliografie1. Hrabok M. M., Hrudey T. M., A review and catalogue of plane bending finite elements. Comput. Structures, 19 (3), 479-495 (1984). 2. Pian H.H., Tong P., Basis of finite element methods for solid continua. Int. J. Numer. Meth. Engng. 1 (1), 3-28 (1969).

9

3.ELEMENTE DE TEORIA ELASTICITIIIntroducereElementele de rezisten ale unei structuri sunt n general solide. Un corp solid, la scar microscopic se compune din molecule, atomi, nuclee, electroni etc. Studiul corpurilor la scar microscopic, pentru a obine comportarea de ansamblu, este dificil de abordat. Este posibil ns, s se dezvolte o teorie fundamentat pe legi matematice i fizice a mediului considerat continuu, care este verificat de comportarea experimental a solidului deformabil. De obicei aceast teorie se completeaz cu o serie de ipoteze simplificatoare. Dac comportarea materialului, for - deformaie, este descris de o relaie elastic atunci se discut de teoria elasticitii. Dac ns comportarea materialului este n domeniul plastic se discut despre teoria platicitii. n continuare se prezint cteva elemente de baz ale teoriei elasticitii, pentru materiale cu comportare liniar elastic, care se deformeaz foarte puin n prezena unor ncrcri (n domeniul deformaiilor mici), astfel nct ecuaiile de echilibru se consider pentru structura nedeformat. De regul, analiza unei structuri tehnice complexe este un proces iterativ i se face pe ct posibil pe cte un element component din structur sau subansamblu. Pentru aceasta este necesar a se introduce toate efectele corpurilor vecine asupra elementului de analizat. Figura 3.1 prezint un astfel de corp, cruia i se asociaz un sistem de referin cartezian drept XYZ. Solicitrile n general sunt produse de efectul corpurilor vecine (presiuni de contact ntre solide, presiuni cauzate de fluide n contact cu corpul, dilatarea produs de variaia temperaturii) i de forele de inerie (produse de gravitaie, de micarea de translaie accelerat sau micarea de rotaie).

Figura 3.1

Figura 3.2

Definiii i notaiiFore. Aciunea unui corp asupra altui corp definete o for. ntotdeauna forele apar perechi aciune-reaciune i trebuie avut n vedere despre ce fel de fore se discut. n teoria elasticiti forele sunt mrimi vectoriale, cu punctele de aplicaie fixate (vectori legai). Forele de inerie (de volum) se definesc de obicei n sistemul global de axe prin vectorul

{p V } = {p Vx

p Vy

p Vz } ,T

(3.1)

n care p Vx , p Vy , p Vz sunt funcii continue, de obicei pe tot domeniul de analiz.

10

Forele de presiune (de suprafa), care acioneaz numai pe conturul domeniului de analiz, se definesc n sistemul global de axe, sau uneori n sisteme de referin locale, prin vectorul

{p S } = {p Sx p Sy p Sz }T ,n care p Sx , p Sy , p Sz sunt funcii continue pe suprafeele pe care se aplic.

(3.2)

Forele concentrate reprezint suma forelor de presiune (fig. 3.2) care lucreaz pe o suprafa foarte mic n comparaie cu suprafaa total a domeniului de analiz. Acestea sunt mrimi "echivalente" cu care se lucreaz uneori n scopul simplificrii problemei atunci cnd nu intereseaz efectul local i se noteaz

{Fi } = {Fi ,x Fi , y Fi,z }T .

(3.3)

Uneori distribuia forelor de presiune este de aa natur nct se reduce la un torsor echivalent, adic o for concentrat i un moment. Deplasri. Deplasarea definete modificarea poziiei unui punct n raport cu un sistem de referin fix. Ea are o component elastic i una de corp rigid. Cmpul deplasrilor, se definete prin vectorul

{u} = {u v w}T ,

(3.4)

n care u = u(x,y,z), v = v(x,y,z), w = u(x,y,z) reprezint funciile deplasrilor liniare pe cele trei direcii ale sistemului de referin considerat (de obicei, sistemul de referin global). Pentru plci, nveliuri i bare se introduc i rotirile, care mpreun cu deplasrile, formeaz deplasrile generalizate. Tensiuni. Gradul de solicitare al unui corp ntr-un punct (element de volum infinitesimal) se definete prin tensorul tensiunilor care are nou componente, dintre care ase independente. Starea de tensiune ntr-un punct se definete n sistemul de referin global (fig. 3.3.a), sau n alt sistem de referin, prin vectorul tensiunilor independente (deoarece xy = yx , yz = zy i zx = xz )

{} = { x y z xy yz zx }T ,

(3.5)

sau echivalent prin tensiunile principale 1 > 2 > 3 n sistemul de referin rotit X Y Z (denumit al direciilor principale), fa de sistemul de referin global (fig. 3.3.b). Tensiunile sunt normale iar tangeniale.

a. Figura 3.3

b.

11

Deformaii specifice. Similar tensiunilor se definete vectorul deformaiilor specifice

{} = { x y z xy yz zx }T ,

(3.6)

n care sunt deformaii specifice liniare, iar deformaii specifice unghiulare. Se menioneaz c tensiunile i deformaiile specifice sunt mrimi tensoriale. Avnd n vedere simetria acestor mrimi, pentru simplitate, se utilizeaz vectorii asociai prezentai mai sus.

Transformarea mrimilor prin schimbarea axelor de coordonateFie dou sisteme de referin carteziene drepte XYZ i X Y Z , rotite ntre ele, sistemul al doilea fiind definit prin cosinusurile unghiurilor l , m, n dintre perechile de axe, astfel X Y Z l1 m1 n1 l2 m2 n2 l3 m3 n3 n continuare, mrimile notate cu prim reprezint valorile raportate la sistemul de referin notat cu prim, iar celelalte corespund sistemului de referin iniial. Transformarea deplasrilor i rotirilor se efectueaz cu o relaie de forma Axele X Y Z

{u } = []{u} ,n carel1 [ ] = l 2 l 3 m1 m2 m3 n1 n2 , n3

(3.7)

(3.8)

este matricea cosinusurilor directoare. Transformarea tensiunilor se efectueaz cu o relaie de forma

{} = [T ]{} ,n care2 l1 2 l2 2 l [T ] = 3 l 1l 2 l 2 l 3 l l 3 1 2 m1 2 n1

(3.9)2m 1 n 1 2m 2 n 2 2m 3 n 3 m1 n 2 + m 2 n 1 m 2 n 3 + m3n 2 m 3 n 1 + m1 n 3 2n 2 l 2 2n 3 l 3 . n 1l 2 + n 2 l 1 n 2 l 3 + n 3l 2 n 3 l 1 + n 1l 3 2n 1 l 1

2l 1 m 1 2l 2 m 2 2l 3 m 3 l 1 m 2 + l 2 m1 l 2 m3 + l 3m 2 l 3 m1 + l 1 m 3

m2 22 m3

n2 22 n 31

m1m 2 m2m3 m 3 m1

n 1n 2 n 2n3 n 3n1

(3.10)

Transformarea deformaiilor specifice se efectueaz cu o relaie de forma

{} = [T ]{} ,n care

(3.11)

12

2 l1 2 l2 2 l [T ] = 3 2l 1 l 2 2l 2 l 3 2l l 3 1

2 m1

2 n1

l 1 m1 l 2m2 l 3m3 l 1 m 2 + l 2 m1 l 2m3 + l 3m 2 l 3 m1 + l 1 m 3

m1n 1 m2n 2 m3n 3 m1n 2 + m 2 n 1 m 2 n 3 + m3n 2 m 3 n 1 + m1 n 3

m2 22 m3

n2 22 n 31

2m 1 m 2 2m 2 m 3 2m 3 m 1

2n 1 n 2 2n 2 n 3 2n 3 n 1

n 2l 2 n 3l 3 . n 1l 2 + n 2 l 1 n 2 l 3 + n 3l 2 n 3 l 1 + n 1l 3 n 1l 1

(3.12)

Observaie! Pentru transformri ntre sisteme de referin diferite, spre exemplu dintr-un sistem de referin cartezian ntr-un sistem de referin cilindric sau sferic, expresiile matricelor de transformare [T ] i [T ] de mai sus trebuie reformulate.

Relaii ntre deplasri i deformaii specificeDeformaiile specifice liniare i unghiulare se pot determina din funciile deplasrilor. Uneori aceste relaii poart denumirea de condiii de compatibilitate geometric, deoarece se obin din examinarea cmpului deplasrilor. Se consider un element de suprafa dreptunghiular, de dimensiuni infinitesimale dx dy, n starea nedeformat a structurii, ca urmare a solicitrilor, se constat o modificare att a dimensiunilor dreptunghiului ct i a formei lui (fig. 3.4). Dac deplasrile sunt mici rezult c modificarea lungimilor laturilor 01 i 02 ale elementului dx dy, produce deformaiile specifice liniare u v x = , ; y = (3.13) x y

iar modificarea unghiului drept 012 duce la deformaia specific unghiular xy = 1 + 2 = v u . + x y

(3.14)

Pentru un element de volum dx dy dz , aceste relaii se completeaz i se scriu n form matriceal astfel

Figura 3.4

13

x x 0 y 0 z = xy y yz 0 zx z

0 y

0 x z

0

0 0 u z v , 0 w y x

(3.15)

sau n form condensat,

{} = [ ]{u} .Relaii de echilibru (Cauchy)

(3.16)

Dac se consider un element de volum dx dy dz n interiorul unui corp (fig. 3.5), relaiile de echilibru sum de momente pe cele trei axe, conduc la dualitatea tensiunilor tangeniale yx = xy ; zy = yz ;

xz = zx ,

(3.17)

relaii de care s-a inut seama la definiia vectorului tensiunilor; iar sum de fore pe cele trei axe, conduc la relaiile x xy zx + + p vx = 0 ; + x z y xy y yz + + + p vy = 0 ; (3.18) x y z zx yz z + + p vz = 0 , + x z y care se rescriu, avnd n vedere definiiile precedente, n form matriceal condensat

[ ]T {} + {p v } = 0 .

(3.19)

Figura 3.5

Figura 3.6

14

Dac elementul de volum considerat, conine un contur al corpului (fig. 3.6), atunci relaiile de echilibru devin p Sx = l x + m xy + n zx (3.20) p Sy = l xy + m y + n yzp Sz = l zx + m yz + n z

n care l , m i n reprezint cosinusurile directoare ale normalei la contur, n raport cu sistemul global de axe.

Relaii constitutive ale materialuluiRelaiile dintre tensiuni i deformaiile specifice corespunztoare se obin pe cale experimental pentru fiecare material n parte. Funcie de tipul materialului ncercrile experimentale prezint anumite particularitti. Pentru unele tipuri de materiale, ncercrile sunt standardizate, i n urma acestora se obin curbe caracteristice, coeficieni, constante de material etc. De regul, aceste constante sunt dependente de o serie de factori cum ar fi: temperatura, dimensiunile i forma epruvetei de ncercare, calitatea suprafeelor, tehnologia de obinere a materialului, etc. Pentru unele materiale (n special metale) i pentru solicitri care nu depesc anumite limite, ntre tensiuni i deformaii specifice exist o relaie cvasi liniar, de forma

{} = [C]{} ,

(3.21)

n care [C] este matricea de complian a materialului, care se mai numete i matricea coeficienilor de elasticitate. Din relaia (3.21) rezult

{} = [C]1 {} = [D]{} ,1

(3.22)

n care [D ] = [C] este matricea de rigiditate a materialului care se mai numete i matricea proprietilor materialului. Pentru un material anizotrop matricea de complian [C] este simetric i conine 21 de constante independente, adic C11 C12 C13 C14 C15 C16 C 22 C 23 C 24 C 25 C 26 C 33 C 34 C 35 C 36 [C] = . (3.23) C 44 C 45 C 46 Sim C 55 C 56 C 66 Pentru un material ortotrop n coordonate carteziene, cu direciile principale de-a lungul axelor, conform relaiilor generalizate ale lui Hooke, rezult

15

1 E x xy E x xz E [C] = x 0 0 0

yx

Ey 1 Ey yz Ey 0 0 0

zx Ez zy

0 0 0 1 G xy 0 0

0 0 0 0 1 G yz 0

Ez 1 Ez 0 0 0

0 0 0 . 0 0 1 G xz

(3.24)

Din motive de simetrie exist relaiile yx xy = ; Ey Ex

zx xz ; = Ez Ex

zy Ez

=

yz Ey

,

(3.25)

astfel nct din cele 12 constante de material, nou sunt independente. Pentru un material izotrop, innd seama de relaia dintre modulul de elasticitate longitudinal E, transversal G i coeficientul de contracie transversal , adic E , G= (3.26) 2(1 + ) rezult 0 0 0 1 1 0 0 0 1 0 0 0 1 [C] = , (3.27) E 2(1 + ) 0 0 Sim 2(1 + ) 0 2(1 + ) din care, prin inversare, rezult matricea de rigiditate a materialului omogen, liniar i izotrop

1 1 1 E [D] = (1 + )(1 2 ) Sim

0 0 0 1 2

0 0 0 0 1 2

0 0 0 0 . 0 1 2

(3.28)

Observaie! Pentru sistemul de referin cilindric, utilizat pentru structurile axial simetrice, relaiile (3.24) - (3.28) au alte forme.

16

Expresii ale energieiLucrul mecanic. Lucrul mecanic este suma dintre produsul forelor i deplasrile produse pe direciilae lor. n continuare, se are n vedere lucrul mecanic al forelor care produc deplasri elastice, deci se consider c domeniul de analiz nu are deplasri de corp rigid. Forele aplicate unui element de volum dV, pot fi fore exterioare (fore de volum, fore de suprafa sau fore echivalente concentrate) i fore interioare (tensiuni), toate considerate constante. Lucrul mecanic al forelor de volum, se scrieWe = {u} {p V }dV ,V T

(3.29)

similar, lucrul mecanic al forelor de suprafa, rezultWe = {u} {p S }dS ,S T

(3.30)

iar lucrul mecanic al forelor concentrate esteWe = {u i } {Fi } .T i

(3.31)

Energia potenial de deformaie. Un corp liniar elastic, acumuleaz o energie intern, exprimat prin T 1 U = {} {}dV . (3.32) 2 V Energia potenial a forelor exterioare. Aceast energie notat Wp , se definete prinWp = We .

(3.33)

Dac se consider, drept fore exterioare, forele de volum i forele de suprafa, energia potenial a forelor exterioare se scrie T T (3.34) W = {u} {p }dV {u} {p }dS .p

V

V

S

S

Tensiuni iniiale i variaia de temperaturCorpul supus analizei este obinut prin procedee tehnologice i este supus unor tratamente termice sau mecanice care induc n material o distribuie de tensiuni iniiale, care se suprapun peste tensiunile mecanice produse de solicitri. Prezena unor tensiuni iniiale este nsoit de deformaiile corespunztoare, dar este suficient s se cunoasc una dintre ele dac materialul are o comportare liniar elastic. Din cauza unor variaii de temperatur la care lucreaz materialul, acesta se dilat dac temperatura crete sau se contract dac temperatura scade. De obicei se accept o temperatur iniial (de referin) la care corpul nu prezint influene produse de temperatur. Dac dilatarea este liber, corpul i modific dimensiunile (apare { 0 } ) fr apariia unor tensiuni iniiale. Dac dilatarea este total

mpiedicat, atunci, corpul nu poate suferi deformaii, dar apar tensiuni iniiale termice { 0 } . Dac dilatarea este parial mpiedicat, atunci n corp apar att deformaii specifice termice ct i tensiuni termice. De obicei se face o distincie ntre deformaiile i tensiunile termice i cele mecanice, deoarece ele sunt nsumate.

17

n prezena unor tensiuni iniiale { 0 } i a unor deformaii specifice iniiale { 0 } , indiferent de modul de producere, relaia (3.22) se rescrie sub forma

{} = [D]({} { 0 }) + { 0 } .Deformaiile specifice produse de dilatarea liber a unui material ortotrop, sunt date de relaia

(3.35)

{ 0 } = T{ x y z 0 0 0}T

(3.36)

n care x , y , z sunt coeficienii de dilatare termic pe cele trei direcii principale, iar T este variaia de temperatur. Dac n relaia (3.35) se consider tensiunile iniiale { 0 } = {0} i deformaiile specifice mecanice

{} = {0} , efectul variaiei de temperatur pentru un corp cu dilatarea total mpiedicat este {} = [D]{ 0 }{} = { 0 } = E T {1 1 1 0 0 0}T . 1 2

(3.37)

Pentru un material omogen i izotrop x = y = z = i innd seama de relaia (3.28) se obine (3.38)

Observaie ! Variaia de temperatur produce modificri sesizabile ale constantelor elastice ale materialului, ducnd la probleme neliniare. De cele mai multe ori ns, pentru a lucra cu o singur valoare a constantelor de material, n special pentru variaii ale temperaturii apropiate de variaiile temperaturii mediului nconjurtor (circa 50 ) se consider valorile medii ale constantelor, n ipoteza c se cunoate temperatura iniial Ti i variaia ei T . Astfel, pentru coeficientul de dilatare termic al unui material izotrop, deoarece (T ) , n practic, de cele mai multe ori, se lucreaz cu valoarea medie 1 Ti + T m = dT . (3.39) T Ti

Bibliografie1. Cook R.D., Malkus D.S., Plesha M.E., Concepts and Applications of Finite Element Analysis, John Wiley & Sons, University of Wisconsin-Madison, Third Edition, 1989. 2. Pascariu I., Elemente Finite. Concepte-Aplicaii, Editura Militar, Bucureti, 1985.

18

4.SCURT PREZENTARE A METODEI ELEMENTELOR FINITE - PRINCIPIILE FUNDAMENTALEIntroduceren cele ce urmeaz se vor folosi notaiile i relaiile prezentate n capitolul 3. Pentru a facilita prezentarea, unele din relaiile respective sunt reluate, n forma necesar pentru dezvoltrile din acest capitol. Pentru a rezolva o problem independent de timp (analiz static liniar pentru obinerea strii de tensiuni i deformaii), n teoria elasticitii trebuie s se in seama de patru tipuri de ecuaii, care n domeniul liniar elastic al deplasrilor mici sunt: 1. relaii de echilibru (Cauchy), adic pentru orice punct din domeniul de analiz (4.1) [ ]T {} + {p v } = {0} ; 2. relaii de compatibilitate ntre deplasri i deformaii specifice

{} = []{u} ;3. relaii constitutive ale materialului

(4.2)

{} = [C]{} sau {} = [D]{} ;

(4.3)

4. condiii la limit n deplasri i fore (fore de inerie, presiuni, variaii de temperatur, deformaii sau tensiuni iniiale cunoscute, deplasri impuse etc). Ecuaiile difereniale care descriu un fenomen se spune c definesc problema n form "exact" ("strong form"), pentru c ele sunt valabile pentru toate punctele din domeniul de analiz. O funcional, care implicit conine ecuaiile difereniale, se spune c descrie problema n form "slab" ("weak form"), deoarece satisface anumite condiii la nivel global (n sensul unei medieri pe domeniul de analiz). Metoda elementelor finite (MEF) este o metod aproximativ de rezolvare a ecuaiilor cu derivate pariale care se bazeaz pe "echivalarea" mediului continuu printr-un model de calcul discret. Ecuaiile difereniale sunt transformate n ecuaii liniare. Mrimile care definesc o problem prin funcii continue (o infinitate de valori) se limiteaz la un numr finit de necunoscute (grade de libertate), alese arbitrar de analist. Gradele de libertate sunt mrimi (cantitative) independente, utilizate pentru a defini configuraia unui sistem. n MEF gradele de libertate reprezint mrimi utilizate pentru definirea variaiei spaiale a unui domeniu de analiz. MEF este fundamentat teoretic. Din punct de vedere matematic exist mai multe modaliti de a obine relaiile de baz cu care opereaz MEF. Una dintre acestea (n analiza structural) este folosirea n form variaional a energiei poteniale totale. Aceast abordare teoretic este sugestiv i poate fi uor interpretat fizic.

Principiul energiei poteniale totale minimeConfiguraia de echilibru a unui sistem se poate analiza prin intermediul energiei poteniale totale. Energia potenial se exprim n form integral (din punct de vedere matematic poart numele de

19

funcional). O funcional este, aadar, o expresie integral care conine implicit ecuaile difereniale care descriu un fenomen anume. n analiza structural, se folosete de obicei, expresia energiei poteniale totale. Funcionalele se ntlnesc i n descrierea fenomenelor termice, electrice, n unele probleme de curgere a fluidelor, n acustic, etc. Energia potenial total a unui sistem elastic conservativ, , se definete ca suma energiei poteniale de deformaie U i potenialul forelor aplicate din exterior (al sarcinilor) Wp

= U + Wp .

(4.4)

Un sistem se numete conservativ dac lucrul mecanic al forelor aplicate (exterioare) i al forelor interioare este independent de traseul deplasrii, fiind o funcie doar de configuraia iniial i final a cmpului deplasrilor. n figura 4.1 se prezint principiul energiei poteniale totale minime aplicat unui element elastic de tip "arc", pentru obinerea poziiei de echilibru. Se observ c poziia de echilibru x ex se obine pentru d minimul energiei poteniale totale, adic din condiia = 0. dx

Figura 4.1 Din punct de vedere matematic, condiiile la limit pentru o problem sunt de dou tipuri: geometrice (numite adesea cinematice sau eseniale) i naturale (numite i neeseniale). Condiiile la limit geometrice se refer la deplasri i uneori la primele derivate (rotiri , curburi) n timp ce condiiile la limit naturale sunt legate de derivatele superioare ale deplasrilor. Spre exemplu dac se consider grinda de rigiditate constant EI, din figura 4.2.a, condiiile eseniale sunt n sgei i rotiri ( v(0) = 0 i (0) = v(0) = 0 ), iar condiiile neeseniale n for tietoare i moment ncovoietor ( T(l ) = EI v(l ) = P i M(l ) = EI v(l ) = 0 ).

a.

b. Figura 4.2

c.

O funcie de clas Cm (continu i derivabil pn la ordinul m), este admisibil dac satisface condiiile la limit eseniale. Configuraiile deformatelor din figura 4.2.b sunt exemple de funcii admisibile iar cele din figura 4.2.c sunt funcii neadmisibile. Funciile admisibile nu trebuie neaprat s coincid cu forma real a deformatei.

20

Deplasrile virtuale {u} sunt deplasri admisibile, care n plus satisfac urmtoarele condiii: sunt independente de forele aplicate structurii i sunt infinitezimale (li se pot aplica regulile calculului diferenial). Forele aplicate structurii rmn constante pentru exprimarea variaiei energiei poteniale totale fa de poziia de echilibru. Din relaia (4.4), innd seama de relaiile (3.32), (3.34) i (4.3), rezult

=

1 T {} [D]{}dV V {u}T {p V }dV S{u}T {p S }dS . V 2

(4.5)

Principiul energiei poteniale totale se enun astfel: la echilibru, variaia energiei poteniale totale pe deplasri virtuale este zero, sau, matematic = 0 ,

= U + Wp = 0 .

(4.6) (4.7)

Echilibrul stabil mai presupune

2 > 0 .Variaia energiei poteniale de deformaie se obine din (3.32) i (4.3b) prin "derivare" U = V

1 1 {}T [D]{}dV + V {}T [D]{}dV = V {}T [D]{}dV , 2 2

(4.8)

n care s-a folosit relaia

matricei de rigiditate a materialului, adic [D] = [D] . Variaia energiei poteniale a forelor exterioare se obine din (3.34)T

({} [D]{})T

T

= {} [D] {} = {} [D]{} i proprietatea de simetrie aT T T

Wp = {u} {p V }dV {u} {p S }dS .T T V S

(4.9)

Metoda de aproximare Rayleigh-RitzAplicarea metodei Rayleigh-Ritz unei funcionale face ca ea s nu mai conin expresii integrale. De regul aceasta duce la un sistem de ecuaii algebrice liniare. Dac funcia necunoscut, respectiv deplasarea, se nlocuiete cu o funcie admisibil, definit prin intermediul unor parametri, atunci din relaia (4.6) se pot gsi valorile lor pentru parametrii care, funcia admisibil aleas aproximeaz cel mai bine funcia exact.Exemplul 1. Se consider grinda de rigiditate constant EI, simplu rezemat din figura 4.3, ncrcat cu o sarcin uniform distribuit. Dac se dorete obinerea sgeii maxime (neglijnd efectul forei x tietoare), se poate alege drept funcie admisibil v(x ) = v m sin , care satisface condiiile la limit l eseniale.

Figura 4.3

Figura 4.4

21

n expresia (4.5) se pun n eviden: {u} = v(x ) , {p V } = 0 , {p S } = u = y dv , dV = dA dx , dS = b dx , I = y 2 dA . A dx Expresia potenialului (4.5) devine2

p du , [D] = E , {} = x = , b dx

2 1 x x = EI v m 2 sin 2 dx pv m sin dx . l l l l 2 l 4 d 4 pl = 0 , se obtine v m = 5 . Efectund calculele, din condiia dv m EI Pentru alte funcii de aproximare se obin alte valori (tabelul. 4.1). Expresia exact a sgeii maxime 5 pl 4 este v m = i se obine dac funcia admisibil coincide cu funcia exact. Deci, dac se alege 384 EI o funcie admisibil adecvat, metoda aproximativ Rayleigh-Ritz poate conduce la soluii exacte.Funcia de aproximare x v(x ) = v m sin l x x v ( x ) = v m 1 l l x x x x2 v ( x ) = v m 1 1 2 l l l l Sgeata maxim vm pl 4 0.013071 EI pl 4 0.010416 EI pl 4 0.0130208 EI Tabelul 4.1 Eroarea relativ a sgeii [%] +0.39

-20.00 0

Exemplul 2. Pentru grinda din figura 4.4, ecuaia fibrei medii deformate se aproximeaz cu polinoame de ordinul doi, trei, patru i cinci. Aplicnd metoda Rayleigh-Ritz, sgeata maxim v m se obine pentru x = x 0 i se prezint n tabelul 4.2. Pentru polinomul de ordinul trei, calculele decurg astfel: - deoarece v (0) = v (l ) = 0 , rezult c polinomul are doar dou constante independente; - alegnd polinomul v (x ) = (c l + d l 2 )x + c x 2 + d x 3 , prin eliminarea constantelor a i b, rezult v (x ) = 2c + 6d x ; - nlocuind n expresia energiei poteniale totale rezult 2 1 = EI(2lc 2 + 6lcd + 6l 3 d 2 ) p l 3 c l 4 d ; 15 12 = 0 i = 0 , conduc la sistemul de - condiiile de minim pentru energia potenial total, c d ecuaii liniare pl 3 EI(4lc + 6l 2 d ) + =0 12 4 EI(6l 2 c + 12l 3 d ) + 2pl = 0 15 2 pl pl i d = 0.00277778 ; de unde rezult c = 0.0166667 EI EI

22

pl 0.0194445l 2 x 0.0166667lx 2 0.00277778x 3 , iar EI v(x ) = 0 , adic pentru x m = 0.516611l i are valoarea sgeata maxim se obine pentru - expresia fibrei deformate devine v (x ) = pl 4 . EI Deci, metoda Rayleigh-Ritz conduce ctre un sistem de ecuaii liniare n care necunoscute sunt parametrii care definesc funcia aleas pentru aproximare. Tabelul 4.2 Funcia de aproximare Poziia Eroare rel. Eroare rel. Sgeata maxim x0 x 0 [%] vm v m [%] v max = v (x m ) = 0.00521412v(x ) = a + b x + c x 2v(x ) = a + b x + c x 2 + d x 3v (x ) = a + b x + c x 2 + d x 3 + e x 4v( x ) = a + b x + c x 2 + d x 3 + e x 4 + f x 5

(

)

0.5 l 0.516611 l 0.511097 l 0.51933 l

-3.72 -0.52 -1.58 0

pl 4 EI pl 4 0.00521412 EI pl 4 0.00651427 EI pl 4 0.00652219 EI

0.00520833

-20.14 -20.05 -0.12 0

Metoda elementelor finite: variant localizat a metodei Rayleigh-RitzDeoarece alegerea unei funcii de aproximare valabil pe ntreg domeniul de analiz nu se poate adopta dect n anumite cazuri particulare, metoda elementelor finite, lucreaz cu funcii de aproximare pe subdomenii (elemente finite, n total NE). n virtutea proprietiilor integralelor sau a nsumrii energiilor componentelor, energia potenial total (pentru toate cele NE elemente finite), se exprim astfel = e ,e =1 NE

(4.10)

iar principiul energiei poteniale totale minime devine

e =1

NE

e

= 0.

(4.11)

Deoarece energia potenial total a unui element este strict pozitiv, din relaia (4.11) rezult

e = 0 ,

(4.12)

relaie care st la baza ecuaiei statice a fiecrui element finit, din mprirea pe subdomenii (discretizare). Domeniul de analiz se poate discretiza n elemente de acelai tip (de exemplu elemente de plac, triunghiulare, cu trei noduri) sau n elemente finite de tipuri diferite (bare, plci i blocuri). Pentru fiecare tip de element finit se face o investigare matematic separat. Cmpul deplasrilor pentru un element finit {u e (x , y, z )} se aproximeaz prin funcii admisibile [N(x, y, z )] denumite funcii de interpolare sau funcii de form, valabile pe tot domeniul elementului. Aceste funcii conin ca parametri valorile coordonatelor nodurilor elementului. Dac deplasrile nodale sunt {U e }, atunci {u e (x , y, z )} = [N e (x , y, z )]{U e }, sau n form condensat

{u} = [N ]{U e } ,de unde rezult

(4.13)T

{u} = [N ]{U e }; {u}T = {U e } [N ]T .23

(4.14)

Deoarece {} = [ ]{u} , rezult

{} = [ ][N ]{U e } = [B]{U e } ,i

(4.15)T

[B] = [][N] ; {} = [B]{U e }; e = e T T e e T T

{}T = {U e } [B]T .e T

(4.16)

Folosind relaiile (4.13) - (4.16) ecuaia (4.12) devineVe

{U } [B ][D][B]{U }dV {U } [N] {p }dV {U } [N] {p }dS = 0 .T Ve V Se S T

(4.17)

Deoarece {U e } este o deplasare virtual nenul, independent de solicitare, iar {U e } este constant, relaia (4.17) se rescrie sub forma

{U } ( [B] [D][B]dV ){U } = {U } ( [N] {p }dV + [N] {p }dS),e T T e e T T T Ve

Ve

V

Se

S

(4.18) (4.19) (4.20)

sau n care

[K ]{U } = {F },e e e

[K ] = [B] [D][B]dV ,e T Ve

este matricea de rigiditate a elementului finit, iar

{F } = [N] {p }dV + [N] {p }dS = {F }+ {F },e T T Ve V Se S e i e p

(4.21)

este vectorul forelor nodale echivalente ale elementului, care asigur condiiile de echilibru ale elementului. Vectorul forelor (4.22) {Fie } = e [N]T {p V }dV ,V

reprezint fora echivalent produs de ncrcarea sarcinilor de volum (de inerie, de obicei). Vectorul forelor nodale al elementului

{F } = [N] {p }dS ,e p T Se S

(4.23)

reprezint fora echivalent produs elementului cu sarcini distribuite sau presiuni care provin att din ncrcrile exterioare (pe conturul domeniului de analiz) ct i din forele interioare de legtur ntre elemente. Dac elementele vecine satisfac anumite cerine, din motive de continuitate (sau datorit principiului aciunii i reaciunii), suma forelor nodale ntr-un nod interior domeniului de analiz este zero. Din acest motiv, forele echivalente produse de presiune se evalueaz doar pentru presiunile care lucreaz pe contururile exterioare. Dac exist fore concentrate care nu lucreaz direct n noduri, acestea se echivaleaz n noduri, conform relaiei (4.24) {Fce } = [N]T {Fi } i se adun la {F } .e

i

Proprietile matricei de rigiditate a unui element finitMatricea de rigiditate a elementului finit este "piatra de temelie" a metodei elementelor finite. Precizia metodei este "dictat" de calitatea acesteia. Fiecare tip de element finit trebuie conceput

24

(proiectat) astfel nct s satisfac ct mai bine anumite cerine. Nu este posibil a se obine un element finit "universal valabil", care s poat modela orice form geometric, s aib un numr oarecare de noduri i de grade de libertate, s includ orice comportare (lege) de material etc. Din acest motiv, de regul, un tip de element finit satisface numai o parte dintre multiplele cerine dictate att de domeniul de analiz i fenomenele descrise de ecuaiile difereniale pe care le rezolv "aproximativ" ct i de dorinele multiple ale utilizatorului. Proiectarea elementului finit se face n anumite ipoteze simplificatoare, iar limitrile performanelor lui sunt generate att de anumite aspecte matematice ct i numerice. Elementele finite trebuie s satisfac anumite cerine eseniale care "asigur" convergena, stabilitatea numeric, soluii ct mai precise pentru discretizri mai puin fine etc. Pentru a concepe un element finit se stabilesc anumite cerine considerate fundamentale i apoi se au n vedere aspecte ct mai general posibile a fi satisfcute din punct de vedere practic, fr un efort "deosebit" din punct de vedere matematic i informatic. De exemplu, pentru un element finit structural patrulater plan cu patru noduri, care prezint dou grade de libertate pe nod, este de dorit ca elementul s poat avea o form oarecare, s poat modela att stare plan de tensiune ct i stare plan de deformaie eventual structuri axial simetrice, s poat include opiuni pentru neliniariti de material, deplasri mari, materiale ortotropice etc. De obicei "performanele" elementelor finite sunt direct proporionale cu funciile de interpolare alese pentru aproximare. Acestea ns nu se pot alege la ntmplare, de obicei funciile de form se aleg din clasa polinoamelor, ntre numrul total de noduri a elementului i gradul polinomului de interpolare este o legtur direct. Astfel dac elementul finit mai sus menionat, are patru noduri i dou grade de libertate n fiecare nod: deplasare pe cele dou direcii ale unui sistem de referin, atunci deplasarea pe fiecare din cele dou direcii (u i v) se poate aproxima "corect" prin polinomul u (x , y ) = a1 + a 2 x + a 3 y + a 4 xy ; v(x , y ) = b1 + b 2 x + b 3 y + b 4 xy deoarece exist opt constante a i i b i , i = 1,,4 i tot attea condiii la limit n noduri, adic deplasarea pe fiecare direcie n fiecare nod reprezint necunoscutele nodale u i i v i , i = 1,,4. Polinomul de interpolare nu se poate alege la ntmplare, deoarece elementul finit trebuie s satisfac o serie de cerine fundamentale cum ar fi: s poat reprezenta micarea de corp rigid i starea de tensiuni constant. Pentru aceasta polinomul de interpolare trebuie s conin termenul liber i cei liniari, de obicei un polinom de interpolare pentru o problem plan se formeaz din triunghiul lui Pascal 1x x2 xy y y2

x3 x2y xy 2 y3 astfel nct, termenii reinui corespund, pe ct posibil, triunghiului de vrf. Dac dintr-o anumit linie nu sunt necesari toi termenii, atunci se aleg termeni simetrici fa de vertical, deoarece altfel elementul prezint izotropie geometric (adic comportarea elementului este funcie de poziia lui n sistemul de referin). Atunci cnd polinomul de interpolare conine toi termenii unui triunghi superior se spune c acesta este complet. Matricea de rigiditate a elementului se obine din relaia (4.20), uneori aceast expresie integral conduce la o expresie algebric simpl (explicit), n care intervin parametrii de definiie a formei elementului i constantele materialului, ns, n general, aceast integral este evaluat numeric deoarece practic nu este posibil a obine formul algebric de calcul. Matricea de rigiditate a elementului K e are urmtoarele proprieti: -simetrie fa de diagonala principal (ca urmare a teoremei reciprocitii forelor); -termeni pozitivi pe diagonala principal; -dimensiunea matricei este egal cu produsul dintre numrul total de noduri a elementului i numrul de grade de libertate pe nod;

[ ]

25

-matricea este singular, (deficient de rang pentru c trebuie s reprezinte micarea de corp rigid, uneori, din motive de integrare ea poate s prezinte i micri de mecanism), se mai spune c matricea de rigiditate a elementului este semipozitiv definit. Semnificaia fizic a elementelor K ij ale matricei K e este cea de fore nodale produse de deplasri

[ ]

unitate.

Asamblarea ecuaiilor de echilibru ale elementelorFolosind relaia (4.11) pentru ntreg domeniul de analiz, n care se nlocuiete (4.19), se obine

{U } [K ]{U } {U } {F } = 0 .NE e T e e NE e T e e =1 e =1

(4.25)

Dac vectorul deplasrilor nodale ale fiecrui element {U e } se exprim funcie de vectorul deplasrilor corespunztor ntregului domeniu de analiz {U} , prin intermediul matricei de ~ conectivitate T e adic

[ ]

~ {U } = [T ]{U} , ~ ~ se obin relaiile {U } = [T ]{U}; {U } = {U} [T ]e ee ee T T

(4.26) care nlocuite n (4.25) conduce laT

e T

~ T ~ T ~ {U} [T e ] [K e ][T e ]{U} {U} [T e ] {F e } = 0 ,NE T NE e =1 e =1

(4.27)

de unde rezult (deoarece {U} {0} ) ecuaia global de echilibru (pentru ntreg domeniul)T

[K]{U} = {F},

(4.28)

n care [K] este matricea de rigiditate a structurii i se obine prin asamblarea matricelor de ~ rigiditate ale elementelor (adunarea matricelor de rigiditate "expandate" ale elementelor, K e ):

[ ]

~ [K ] = [K e ] ;NE e =1

~ ~ ~ [K ] = [T ] [K ] [T ].e e T e e

(4.29)

{F} este vectorul ncrcrilor nodale al structurii i se obine prin asamblarea ncrcrilor echivalente ~ ale elementelor (adunarea ncrcrilor "expandate" ale elementelor F e , n care se includ numai forele exterioare):

{ }

{F} = {~ e }; FNE e=1

~ {~ }= [T ] {F }. Fe e T e

(4.30)

Practic asamblarea se realizeaz fr "expandarea" matricelor de rigiditate i a vectorilor ncrcrilor, prin aa numita asamblare direct, care ine seama de matricea de conectivitate a structurii. Dac matricea de rigiditate i vectorul forelor echivalente n nodurile elementeului se determin ntr-un sistem de referin diferit de sistemul de referin global (n sistemul de referin local al elementului) atunci matricea de rigiditate a elementului n coordonate globale [K e ] se obine din maticea de rigiditate n coordonate locale [k e ] folosind relaia de transformare

[K ] = [T ] [k ][T ] ,e e T e e

(4.31)

26

similar, vectorul forelor {F e } se obine din {f e } prin

{F } = [T ] {f },e e T e

(4.32)

n care [T e ] este matricea de rotaie a coordonatelor, de aceeai dimensiune ca matricea de rigiditate i care conine pe diagonal blocuri ale matricelor cosinusurilor directoare [ i ] (vezi relaia (3.8)).

Efectul tensiunilor iniiale i efectul termoelasticDac modelul de analiz are o distribuie iniial de tensiuni nenule cunoscute { 0 } sau sufer o variaie de temperatur T , atunci ecuaiile de echilibru ale elementului finit se modific. Astfel, considernd ecuaia (3.35) n locul ecuaiei (4.3b), energia potenial intern (3.32) rezult U= 1 T {} [D]{}dV V {}T [D]{ 0 }dV + V {}T { 0 }dV V 2 (4.33)

care duce la apariia unor ncrcri suplimentare cu fore echivalente, adic fore generate de deformaiile specifice iniiale (de obicei produse de variaia de temperatur)

{F } = [B] [D]{ }dV ,e T Ve 0

(4.34)

i fore generate de tensiunile iniiale {Fe } =

Ve

[B]T { 0 }dV .

(4.35)

Aceste fore se adun la vectorul forelor echivalente al elementului finit {F e } .

Efectul fundaiilor elasticeAnumite elemente finite, n special elementele de plac (fig. 4.5) i bar, permit introducerea unor condiii la limit, de tipul rezemrilor elastice, nc din formularea ecuaiei de echilibru a elementului finit.

Figura 4.5 n general, se consider c presiunea exercitat de fundaie asupra elementului finit este proporional cu deplasarea normal n fundaie prin coeficientul de rigiditate k w [N/m3], adic p f = k w w , sau n form matriceal (4.36) {p f } = k w {u} . Energia potenial suplimentar a forelor exterioare (presiunea p f ) esteWp ,f = e {u} {p f }dS f .T Sf

(4.37)

27

Dac pentru aproximarea deplasrii se alege expresia

{u} = [N n ]{U e },Wp ,f = {U e } k w e [N n ] [N n ]dS f {U e }T T Sf

(4.38)

n care [N n ] reprezint funciile de form pentru aproximarea deplasrii normale la plac, se obine

(

)

(4.39

de unde rezult o component suplimentar a matricei de rigiditate a elementului, generat de efectul fundaiei (4.40) [K ef ] = k w e [N n ]T [N n ]dSfSf

care se adun la matricea de rigiditate definit prin relaia (4.20).

Efectul ncrcrii cu fore de inerieVectorul forelor de volum, generate de o micare accelerat (sau gravitaie), se exprim prin 2 {u} 2 {U e } {p V } = 2 = [N ] 2 t t

(4.41)

nodal care se noteaz

2 {U e } && e = {U }, este conoscut (spre exemplu acceleraia gravitaional), t 2 atunci din relaia (4.22) se obine

n care s-a inut seama de relaia (4.13). Dac densitatea materialului este constant i acceleraia

&& && {F } = ( [N] [N]dV ) {U } = [M ]{U }e i T e e e Ve

(4.42) (4.43)

n care

[M ]= [N] [N]dV ,e T Ve

este matricea de mas (coerent) a elementului finit.

Metoda deplasrilorMetoda deplasrilor s-a dezvoltat cu mult nainte de metoda elementelor finite i a fost aplicat structurilor complexe formate din bare articulate i grinzi. La nceput metoda elementelor finite s-a inspirat din metoda deplasrilor, iar n momentul de fat aceasta (metoda deplasrilor) poate fi privit ca un caz particular al metodei elementelor finite, fiind o metod exact pentru calculul static al structurilor din bare drepte. Prezentarea metodei deplasrilor constituie pentru cititorul care stpnete elementele de baz din rezistena materialelor o mai uoar nelegere a unor noiuni de baz cum ar fi matricea de rigiditate a unui element i asamblarea matricei de rigiditate a structurii. Se consider o structur simpl din bare articulate n plan, pentru care se prezint modul de obinere a matricei de rigiditate a elementului n coordonate locale i globale, modul de asamblare a matricei de rigiditate a stucturii, impunerea condiiilor la limit i rezolvarea problemei pentru o analiz static. Structura din figura 4.6.a, raportat la sistemul global de referin XOY, este format din cinci bare articulate n plan. Cunoscnd lungimea l , ariile barelor de parametru A, modulul de elasticitate longitudinal E, constant la toate barele, i valoarea parametrului F care definete forele, se cere s se determine deplasrile nodurilor, reaciunile n reazeme i forele axiale (eforturile) n bare.

28

Nodurile i elementele structurii se numeroteaz ca n figura 4.6.b, adic structura se discretizeaz. Dac se face abstracie de ncrcri i rezemri, n fiecare nod (fig. 4.6.c) se pot defini forele care ar putea s acioneze asupra structurii, izolate din eventualele legturi cu exterioru. Similar, fiecare nod poate avea o deplasare n lungul axei X i Y (fig. 4.6.d). Se observ c toate mrimile (considerate pozitive) s-au figurat n sensul pozitiv al axelor, pentru a uura implementarea metodei deplasrilor ntr-un algoritm uor de programat. Forele i deplasrile din figurile 4.6.c, d, definesc vectorul ncrcrilor nodale {F}, respectiv vectorul deplasrilor nodale {U}, pentru ntreaga structur

Figura 4.6

Figura 4.7

FX1 U1 FY1 V1 FX 2 U 2 F V 2 Y2 {F} = ; {U} = . (4.44) FX 3 U3 FY 3 V3 FX 4 U 4 F V Y4 4 Legtura dintre cei doi vectori urmeaz a fi realizat prin matricea de rigiditate global a structurii [K], de dimensiune 8 8, care se obine din matricele de rigiditate ale elementelor. Pentru a obine matricea de rigiditate a unui element oarecare de bar articulat n plan (TRUSS2D), se consider o bar oarecare cu nodurile la capete I i J (fig. 4.7.a) care face un unghi cu axa sistemului global de referin OX. Elementului i se definete sistemul propriu de referin, adic sistemul de axe xoy, n care axa ox este axa barei. Pentru acest element se consider c seciunea lui este constant de valoare A, bara este dintr-un singur material, cu modulul de elasticitate longitudinal E, lungimea elementului este L, forele preluate de element sunt numai forele axiale (notate N), ceea ce nseamn c elementul face parte dintr-o structur n care legturile dintre bare sunt articulaii plane perfecte. De asemenea se consider c elementul este ncrcat numai cu fore n nodurile sale i deformaiile lui sunt mici, ceea ce se traduce prin faptul c ecuaiile de echilibru scrise pentru elementul nedeformat sunt aceleai i pentru elementul deformat. Forele din nodurile elementului n sistemul de referin global se noteaz cu litere mari, iar n sistemul de referin local cu litere mici

29

(fig. 4.7.a), similar deplasrile (fig. 4.7.b). Se observ c n sistemul de referin local, conform ipotezelor enunate, elementul prezint fore i deplasri numai n lungul axei ox. n concordan cu aceste notaii, pentru elementul finit supus analizei, se pot defini forele {Fe } i deplasrile {U e } din noduri, n sistemul de referin global FxI UI V FyI (4.45) e e {F } = ; {U } = I . U J FxJ VJ FyJ e e Similar se pot defini forele {f } i deplasrile {u } n sistemul de referin local f xI f I u I v f yI 0 (4.46) {f e } = = ; {u e } = u I . f xJ f J J v J f yJ 0 Este mult mai simplu s se obin matricea de rigiditate a elementului n coordonate locale, fr a NL . face apel dect la cunotinele de baz din rezistena materialelor, adic L = EA Avnd n vedere notaiile, rezult c fora axial din bar i lungirea ei, se poate exprima NL L = ; N = f I = f j ; L = u J u I , (4.47) EA relaii din care rezult EA fI = (u I u J ) L . (4.48) EA fJ = (u I u J ) L Considernd relaiile de definiie (4.46), mpreun cu relaiile (4.48), se poate scrie 1 0 1 0 u I f xI E A 0 0 0 0 v I f yI (4.49) = , L 1 0 1 0 u J f xJ 0 0 0 0 v f J yJ relaie n care se pune n eviden matricea de rigiditate [k e ] a elementului n coordonate locale1 EA0 e [k ] = L 1 0 0 1 0 0 0 0 . 0 1 0 0 0 0

(4.50)

este matricea de transformare a vectorilor deplasri i fore din sistemul de referin local la cel global. Particularizarea acestei matrice de transformare (vezi relaia general (3.8) pentru 3D, care se consider n 2D pentru dou noduri), conduce la

[K ] = [T ] [k ][T ], n care [T ]e e T e e e

Pentru a obine matricea de rigiditate n coordonate globale se folosete relaia (4.31), adic

30

0 0 c cos sin 0 0 s sin cos e [T ] = = 0 cos sin 0 0 0 sin cos 0 0

0 c 0 0 , 0 c s 0 s c s 0

(4.51)

n care s-a inut seama de relaiile trigonometrice cos = sin , cos + = sin i s-a notat 2 2 c = cos , s = sin . Din relaia (4.31), prin nlocuirea relaiilor (4.50) i (4.51) rezult matricea de rigiditate a elementului de bar articulat 2D, n coordonate globale c2 cs c 2 cs s 2 cs s 2 EA cs (4.52) [K e ] = L 2 , 2 e c cs c cs 2 cs s2 cs s EA n care prin se nelege c toate mrimile aparin elementului. L e Relaia (4.52) se poate aplica pentru toate elementele modelului considerat. Se poate creea tabelul 4.3 cu datele proprii fiecrui element, ceea ce simplific operaia de identificare a parametrilor respectivi, adic Tabelul 4.3 Nod EA Elem. I J c s cs Le Ae E e L e o c2 s2 l 1 1 2 0 1 0 1 0 0 A E EA l l 2 2 3 0 1 0 1 0 0 A E EA l l 0 1 0 0 1 3 2 4 2A E EA 90o 2 l 4 1 4 EA 1 1 1 45o 2l 2 2A E 2 2 2 l 2 2 2 2 2 5 3 4 EA 1 1 1 135o 2l 2 2A E 2 2 2 l 2 2 2 2 2 Matricele de rigiditate ale elementelor, n coordonate globale sunt:1 EA 0 1 2 [K ] = [K ] = l 1 0 0 1 0 0 0 0 ; 0 1 0 0 0 0 0 0 EA 0 2 3 [K ] = l 0 0 0 2 0 0 2 ; 0 0 0 2 0

31

1 1 1 1 EA 1 1 1 1 4 [K ] = l ; 1 1 1 1 1 1 1 1

1 1 1 1 EA 1 1 1 1 5 [K ] = l . 1 1 1 1 1 1 1 1

Matricele de rigiditate ale elementelor se expandeaz n vederea asamblrii, pentru aceasta se ~ ~ T ~ folosete relaia (4.29b), adic K e = T e [K e ] T e , n care matricele de conectivitate fac legtura ntre gradele de libertate ale elementului i gradele de libertate a structurii. Din acest motiv aceste matrice conin doar valori nule sau unitate. De exemplu pentru elementele 3 i 4, matricele de conectivitate sunt 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 ~ 3 0 0 0 1 0 0 0 0 ~ 4 0 1 0 0 0 0 0 0 T = T = ; , 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1

[ ] [ ]

[ ]

[ ]

[ ]

~ deoarece se poate verifica cu uurin c {U e } = T e {U} . Matricele de rigiditate expandate ale celor cinci elemente sunt:1 2 3 4

[ ]-1 0 1 0 0 0 0 0

~ [K ] = EA l1

1 0 -1 0 0 0 0 01

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 01

0 0 0 0 0 0 0 02

0 0 0 0 0 0 0 03

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 03

0 0 0 0 0 0 0 04

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 04

1 2 3 4

~ [K ] = EA l2

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0 0 1 0 -1 0 0 02

0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 -2

0 0 -1 0 1 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

1 2 3 4

~ [K ] = EA l3

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 -2 0 0 0 2

1 2 3 4

32

1

2

3

4

~ [K ] = EA l4

1 1 1 1 0 0 0 0 0 0 0 0 -1 -1 -1 -11

0 0 0 0 0 0 0 02

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 03

0 0 0 0 0 0 0 0

-1 -1 1 -1 -1 0 0 2 0 0 0 0 3 0 0 1 1 4 1 14

~ [K ] = EA l5

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0

0 0 0 0 1 0 0 0 0 0 0 0 0 2 0 0 0 0 1 -1 -1 1 3 -1 1 1 -1 -1 1 1 -1 4 1 -1 -1 1

Matricea de rigiditate global (a structurii) rezult1 2 3 4 1 2 3 4

[K ] = [5 e =1

2 1 -1 0 0 0 -1 -1 1 1 0 0 0 0 -1 -1 -1 0 2 0 -1 0 0 0 EA 0 0 0 2 0 0 0 -2 ~ Ke = l 0 0 -1 0 2 -1 -1 1 0 0 0 0 -1 1 1 -1 -1 -1 0 0 -1 1 2 0 -1 -1 0 -2 1 -1 0 4

]

.

Ecuaiile de echilibru global incluznd condiiile la limit n deplasri U1 = V1 = V3 = 0 i condiiile la limit pentru fore (ncrcri) FX 2 = 0 ; FY 2 = 2F ; FX 3 = 0 ; FX 4 = F ; FY 4 = 0 , se scrie1 2 3 4

2 1 -1 EA 0 l 0 0

1 1 0 0 0 0

-1 0 2 0 -1 0 0 0

0 0 0 2 0 0

0 0 -1 -1 0 0 -1 -1 -1 0 0 0 0 0 0 -2 . 2 -1 -1 1 -1 1 1 2 0 -1 0 4

0 0

U2 V2 U3 0 U4 V4

FX1 FY1 0 -2F = 0FY 3 F 0

1 2

.3

-1 -1 -1 -1

0 -1 1 -2 1 -1

4

Se observ c n nodurile n care se cunosc deplasrile nu se cunosc reaciunile i acolo unde se cunosc ncrcrile nu se cunosc deplasrile. Aadar, considernd ecuaiile corespunztoare liniilor albe

33

(liniile i coloanele corespunztoare deplasrilor nule - liniile negrite se "taie" sau se elimin) rezult un sistem de cinci ecuaii, cu cinci necunoscute [K r ]{U r } = {Fr } , adic0 1 0 0 U 2 0 2 2 0 0 2 V2 2F 0 EA 2 1 1 U3 = 0 . 1 0 l 0 0 1 2 0 U 4 F 0 2 1 0 4 V4 0

Rezolvarea acestui sistem conduce la soluiile Fl Fl Fl U 2 = 1.5 V2 = 3.5 ; ; U3 = 3 ; EA EA EA

U4 = 2

Fl ; EA

V4 = 2.5

Fl . EA

Pentru a obine reaciunile, se consider doar ecuaiile corespunztoare liniilor negrite, deoarece o parte din termenii ecuaiilor se nmulesc cu deplasri nule (se consider termenii ncadrai i negrii mai accentuat), adic U 2 FX1 1 0 0 1 1 V2 F EA FY1 = 0 0 0 1 1 U 3 = 0.5 F . l FY 3 0 0 1 1 1 U 4 1.5 F V4

{f } = [k ]{u } = [k ][T ]{U }. De exemplu, pentru elementul 4, se obinee e e e e e

Pentru calculul eforturilor n bare se reconsider ecuaiile de echilibru ale elementului finit 1 0 0 0 1 0 0 0 2 2 2 2 0 0 2 2 2 2 0 0 0 0 2 2 2 2 0 0 2 F 0 2 0 F l 0 . 2 E A = 2 2 F Fl 2 2 2.5 2 E A 0 2 2 3 2 F ; N5 = F. 2 2

N 4 1 0 EA 0 4 =2 l 1 N 0 0

0 0 0 0

Similar pentru toate barele. Rezult: N1 = 1.5 F ; N 2 = 1.5 F ; N 3 = 2 F ; N 4 =

Elementul finit patrulater plan, cu patru noduriUnul dintre cele mai folosite elemente finite pentru modelrile plane, este elementul izoparametric cu patru noduri (fig. 4.8.a). Acesta este definit n sistemul de referin global XOY de nodurile I, J, K, L (notate n continuare pentru simplificarea expunerii, cu 1, 2, 3, 4), i are dou grade de libertate pe nod, adic deplasrile n lungul axelor X i Y. Att deplasrile ct i coordonatele se vor nota cu litere mici, dei ele sunt raportate la sistemul de referin global i ar trebui notate cu litere mari. Geometria elementului este definit de coordonatele nodurilor x i , y i , i = 1, 2, 3, 4 i funciile de interpolare biliniare, n coordonate naturale (fig. 4.8.b)

34

prin formularea

1 (1 )(1 ); 4 1 N 3 = (1 + )(1 + ); 4 N1 = x = Ni x i ;i =1 4

N2 =

1 (1 + )(1 ); 4 1 N 4 = (1 )(1 + ) , 4 y = Ni yi ,i =1 4

(4.53)

(4.54)

care stabilete o relaie de transformare geometric ("mapping") ntre domeniul descris de ptratul de latur 2, n sistemul de referin natural (spaiul ) i domeniul patrulaterului din sistemul de coordonate XOY. Aceast relaie transpune axele sistemului de referin din figura 4.8.b n figura 4.8.a astfel nct acestea rmn linii drepte, trec prin mijloacele laturilor elementului, dar nu mai pstreaz unghiul drept dintre axe i intersecia lor nu corespunde centrului de greutate al patrulaterului de o form oarecare.

Figura 4.8 Cmpul deplasrilor necunoscute se aproximeaz prin aceleai funcii de interpolare (element izoparametric), adic u = Ni u i ;i =1 4

v = Ni vi ,i =1

4

(4.55)

n care u i , v i , i = 1, 2, 3, 4 , sunt deplasrile nodurilor pe direciile axelor OX i OY. Pentru stabilirea matricei de rigiditate a elementului se folosete relaia (4.20), adic T K e = e [B] [D][B]dV , n care [B] = [ ][N] , [D] se obine pentru descrierea 2D a comportrii

[ ]

V

materialului, (vezi relaia (3.28) pentru cazul 3D), iar dV=t dS, n care t este grosimea elementului i dS elementul infinit mic de suprafa. Dac se consider deplasrile nodale descrise de vectorul

{U e }= {u1

v1

u2

v2

u3

v3

u4

T v4} ,

(4.56)

atunci relaia de aproximare matriceal (4.13) {u} = [N ] U e se scrie explicit, folosind relaiile (4.55) astfel

{ }

35

u1 v1 u 2 u N1 0 N 2 0 N 3 0 N 4 0 v 2 (4.57) = . v 0 N1 0 N 2 0 N 3 0 N 4 u 3 v3 u 4 v 4 Problema esenial care apare n relaia de calcul (4.20) a matricei de rigiditate a elementului este c matricea funciilor de form [N] este exprimat n coordonate naturale, iar operatorul de derivare [ ] se aplic n coordonate globale x, y. Deoarece funciile de form N i definite de (4.53) sunt n coordonate naturale , iar x i y conin funciile N i , nseamn c trebuie folosite regulile de derivare a funciilor compuse, care n form matriceal se scriu astfel

x = x

y x x = [J (, )] . y y y

(4.58)

Matricea [J(, )] poart denumirea de jacobianul transformrii, i se noteaz de obicei x [J ] = x y . y

(4.59)

innd seama de relaiile (4.54), jacobianul se poate obine efectund produsul matriceal N1 [J ] = N1 N 2 N 2 N 3 N 3 x1 N 4 x 2 N 4 x 3 x 4 y1 y 2 J11 = y 3 J 21 y4

J12 . J 22

(4.60)

Deoarece n relaia (4.60) intereseaz termenul din dreapta, se obine x 1 = [J(, )] , y unde, pentru calculul inversei jacobianului, trebuie calculat determinantul

(4.61)

det[J ] = J11J 22 J12 J 21 ,i apoi inversa matricei jacobianului

(4.62)

36

[J ]

1

* J11 = J * 21

* J12 1 J 22 = J * det[J ] J12 22

J 21 . J11

(4.63)

Folosind relaiile (4.61) i (4.63) elementele componente ale matricei [ ] n plan devin * * ; = J11 + J12 x . = J* + J* 21 22 y

(4.64)

Matricea operatorilor de derivare (3.15), particularizat pentru 2D, este x [ ] = 0 y 0 . y x

(4.65)

Derivata matricei funciilor de form se exprim n coordonate naturale astfel

* N i * N i + J12 J11 [B] = 0 3 8 N N i i J * + J* 21 22

J* 21

N i N i * J11

* N i + J 22 N i * + J12 i=1 0

i=2

i=3

, i=4

(4.66)

n care s-a scris explicit doar prima partiie a matricei n care N i = N1 . Din relaiile (3.21) i (3.27) rezult matricea de rigiditate a materialului n plan. De exemplu, pentru starea plan de tensiune ( z = 0 , yz = 0 i zx = 0 ), rezult1 0 (4.67) [D] = E 2 1 0 . 1 3 3 0 0 1 2 Elementul de arie se transform prin dS = dx dy = det[J ]d d i astfel expresia matricei de rigiditate n coordonate naturale este

[K ] = [B(, )] [D] [B(, )] t det[J( , )]d d .e 1 1 T 8 8 1 1

(4.68)

Calculul analitic al relaiei (4.68) este complicat. Mai mult, matricea conine 64 de termeni, dintre care 40 trebuie determinai, ceilali obinndu-se din simetria matricei de rigiditate. Din aceste motive se recurg la calculul numeric al acestor integrale. Exist mai multe metode de integrare numeric aproximativ, dar cea care s-a impus n MEF este metoda de integrare Gauss-Legendre.

Integrarea numeric folosind metoda Gauss-LegendreEvaluarea numeric a integralei unei funcii de o variabil I = f (x ) dx decurge astfel:a b

37

b a (1 ) + (1 + ) care transform limitele de integrare ntre 2 2 1 b 1 a 1 i 1; rezult dx = (b a ) d i ( ) = (b a ) f (1 ) + (1 + ) ; 2 2 2 2 1. se face schimbarea de variabil x = 2. integrala se transform n I = ( ) d h i (i ) ; adic ntr-o sum ponderat de n valori ale1 n

1

i =1

funciei de integrat n coordonate naturale . Valoarea lui n se numete ordin de integrare, h i sunt factori de pondere, iar i definesc poziiile punctelor Gauss. Dac funcia de integrat este polinomial, se demonstreaz c pentru polinoame de grad 2n-1, integrarea este exact, altfel integrarea este aproximativ i crete n precizie odat cu creterea ordinului de integrare. n tabelul 4.4 se prezint coordonatele punctelor Gauss i ponderile corespunztoare pentru primele patru ordine de integrare. Figura 4.9 red interpretarea geometric a integrrii pentru primele trei ordine de integrare. Ordinul de integrare n 1 2 3mm

Poziia punctelor Gauss i 0 m 1 3 = m0.577350269189626

Tabelul 4.4 Factori de pondere hi 2 1

m 0.6 = m0.774596669241483 03 + 2 1 .2 = m0.861136311594053 73 2 1 .2 = m0.339981043584856 71 1 n n

4

5 9 = 0.555555555555555 8 9 = 0.888888888888888 1 1 = 0.3478548451 37454 2 6 1 .2 1 1 + = 0.6521451548 62546 2 6 1 .2

Dac funcia de integrat este de dou variabile, atunci n mod similar se arat c

I=

1 1

(, ) d d h i h j (i , j ) .i =1 j=1

(4.69)

Figura 4.9 Revenind la relaia (4.68), pentru calculul matricei de rigiditate, se adopt de obicei integrarea 2 2 sau 3 3, cu patru, respectiv nou puncte de integrare Gauss, care sunt plasate ntr-un element patrulater oarecare ca n figura 4.10. Alegerea ordinului de integrare este o problem delicat. Integrarea cu un numr mic de puncte prezint avantajul unui volum redus de calcul, dar nu asigur precizia sau condiiile pe care trebuie s le ndeplineasc matricea de rigiditate. Pentru o precizie superioar se impune o integrare cu un numr mare de puncte Gauss, ceea ce crete implicit volumul calculului. Integrarea 2 2 este este ns cel mai

38

des folosit, iar uneori pentru elemente patrulatere puternic distorsionate se folosete i integrarea 3 3. Uzual, elementul finit prezentat poart denumirea de Q4.

Figura 4.10 Elementul Q4 prezint unele inconveniente legate n special de "slaba" reprezentare a deplasrii de ncovoiere, adic un element finit supus la ncovoiere (fig. 4.11.a) trebuie s se deformeze ca n figura 4.11.b, dar n realitate se deformeaz ca n figura 4.11.c, deoarece funciile de form alese pentru aproximarea deplasrii sunt liniare pe conturul elementului.

Figura 4.11 Pentru a corecta acest neajuns, elementul Q4 se "mbuntete" prin considerarea a dou funcii de form suplimentare ("extra shape function"), n reprezentarea cmpului de aproximare a deplasrii: N5 = 1 2 ; u = Ni u i ;i =1 6

N 6 = 1 2 v = Ni vi .i =1 6

(4.70)

i se transform n aa numitul element Q6, iar expresiile (4.55) se modific astfel (4.71)

Deplasrile u 5 , u 6 i v5 , v 6 nu corespund unor noduri suplimentare, dar pot fi privite ca deplasri suplimentare ale unor "grade de libertate interioare". Figura 4.12 prezint modul de variaie al funciilor de form considerate att pentru elementul Q4 ct i pentru elementul Q6, precum i variaia cmpului deplasrilor acestora (ntr-un mod oarecare de deformaie). Se observ prin comparaia figurilor 4.12.g i h c funcia necunoscut pe conturul elementului este liniar pentru elementul Q4, i parabolic pentru elementul Q6. Deoarece ecuaia parabolei pe conturul elementului este determinat de gradele de libertate interioare elementului este posibil ca dou elemente vecine s nu prezinte aceeai lege de variaie pe contur, ceea ce face ca elementul Q6 s fie neconform, adic ntre laturile unor elemente vecine pot apare goluri sau suprapuneri. Obinerea matricei de rigiditate a elementului Q6 este similar cu a elementului Q4, cu deosebirea c prezena a ase funcii de interpolare conduce la matricea [B] de dimensiuni 3 12 i n final la o matrice de rigiditate 12 12. Gradele de libertate nenodale nu particip la asamblare i din acest motiv ele nu prezint interes dect n faza de obinere a matricei de rigiditate i mai apoi n calculul tensiunilor i de regul ele se elimin, sau, cu alte cuvinte, se "condenseaz static".

39

a.

b.

c.

d.

e.

f.

g. (Q4) Figura 4.12

h. (Q6)

Condensarea static a gradelor de libertate interioareAcest procedeu de eliminare a unor grade de libertate, este folosit pe scar larg n MEF, i se ntlnete att la nivelul unui element finit, sau al unei substructuri, i chiar n anumite tehnici de rezolvare a sistemelor de ecuaii liniare, cum ar fi metoda de rezolvare frontal a unui sistem de ecuaii liniare. Gradele de libertate ale elementului Q6, care trebuie eliminate, sunt u 5 , v5 , u 6 i v 6 , adic vectorul {U b } din partiionarea ecuaiilor de echilibru a elementului finit[K aa ] [K ba ]

[K ab ] {U a } {Fa } = , [K bb ] {U b } {Fb }{Fa } {F } = {8F1} . 12 1 4b1 e

(4.72)

n care dimensiunile submatricelor i a subvectorilor sunt [K aa ] [K ab ] {U a } 8 4 8 e e 8 8 [1212] = [K ] [K ] ; {U } = {U1 } ; K 12 1 ba bb b 41 4 8 4 4 Ecuaia (4.73) se rescrie n forma

(4.73)

40

[K aa ]{U a } + [K ab ]{U b } = {Fa } ; [K ba ]{U a } + [K bb ]{U b } = {Fb } .

(4.73')

Din ecuaia (4.73'.b) rezult o relaie de legtur ntre deplasrile corespunztoare gradelor de libertate interioare {U b } i deplasrile nodale {U a }

{U b } = [K bb ]1 ({Fb } [K ba ]{U a }) ,care prin nlocuire n relaia (4.73'.a) conduce la

(4.74)

([K

aa

] [K ab ][K bb ]1[K ba ]){U a } = {Fa } [K ab ][K bb ]1{Fb } .

(4.75)

Matricea condensat

[K ] = [K ] [K ][K ] [K ],e c 8 81

aa

ab

bb

ba

(4.76)

n care se regsesc numai gradele de libertate corespunztoare nodurilor elementulu