Algebra si Geometrie

Seminar 2

Octombrie 2017

ii

”Matematica poate fi definita ca materia ın care nu stim niciodatadespre ce vorbim, nici daca ceea ce spunem este adevarat.”

Bertrand Russell

1Spatii vectoriale

Codarea mesajelor

Mesajele transmise, cum ar fi datele provenite de la un satelit, sunt intot-deauna supuse interferentelor. E important asadar sa putem cripta mesajele inasa fel incat, dupa ce sunt alterate de interferente, sa poata fi decriptate la formalor originala. Acest lucru se face uneori prin repetarea mesajului de doua sautrei ori, un lucru de altfel comun si in vorbire. Insa multiplicarea informatiilorstocate intr-un computer va duce la supraincarcarea memoriei acestuia. E im-portant sa incercam sa gasim cai de a decoda mesajele dupa ce sunt distorsionatede interferente. Acest proces se numeste coding. Un cod care detecteaza erorile

1

intr-un mesaj distorsionat de interferente (scrambled message) se numeste de-tector de erori. Daca, in plus, poate corecte erorile se numeste corector deerori.

Tehnici de baza de coding: Cele mai multe mesaje sunt trimise sub formaunui sir digital de 0-uri si 1-ri, ca de exemplu 10101 sau 1010011, asadarsa presupunem ca vrem sa transmitem mesajul 1011. Acest “cuvant” binarpoate reprezenta un cuvant adevarat ca si ”cumpara” sau o intreaga propozitie”cumpara actiuni”. O varianta de criptare a lui 1011 ar fi sa ii atasam o coadabinara in asa fel incat daca mesajul este deformat, sa zicem in 0011, putem sadetectam eroarea. O astfel de coada poate fi 1 sau 0, in functie de numarulde 1-uri din mesaj. Mai precis adaugam un 1 daca avem un numar impar de1-uri in cuvantul binar transmis si 0 daca avem un numar par. In acest fel toatecuvintele criptate vor avea un numar par de 1-uri. Deci 1011 va fi codificat ca si10111. Acum daca acest mesaj este deformat in 00111 stim ca a aparut o eroaredin moment ce avem un numar impar de 1-ri. Aceasta metoda de detectare aerorilor se numeste verificarea paritatii si e prea simpla pentru a fi utila. Deexemplu daca doua cifre sunt schimbate, metoda noastra nu va detecta eroarea.Alta abordare ar fi sa repetam de doua ori mesajul si sa transmitem 10111011.Acum daca 00111011 este receptionat, stim ca una din cele doua copii a fostdeformata. Si aceasta metoda da rezultate slabe si nu este prea des folosita.

O tehnica avansata de codare: codul HammingIn anii 50′ R.H. Hamming a introdus o metoda de corectare a unei singure eroricare e acum cunoscuta ca find codarea Hamming. Pentru a examina detaliileacestei tehnici avem nevoie de cateva notiuni de algebra liniara.

Spatii vectoriale peste corpul K = Z2

Multimea Z2 = {0, 1} a resturilor la impartirea cu 2 impreuna cu adunareasi inmultirea definite mai jos:

0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 0, 0 + 0 = 0

0 · 1 = 0, 1 · 0 = 0, 1 · 1 = 1, 0 · 0 = 0

formeaza un corp.Reamintim ca structura de spatiu vectorial a lui R𝑛 este data de adunarea

vectoriala:

(𝑥1, 𝑥2, . . . , 𝑥𝑛) ⊕ (𝑦1, 𝑦2, . . . , 𝑦𝑛) := (𝑥1 + 𝑦1, 𝑥2 + 𝑦2, . . . , 𝑥𝑛 + 𝑦𝑛)

si inmultirea cu scalari:

𝜆⊙ (𝑥1, 𝑥2, . . . , 𝑥𝑛) := (𝜆𝑥1, 𝜆𝑥2, . . . , 𝜆𝑥𝑛)

pentru 𝑥1, 𝑥2, . . . , 𝑥𝑛, 𝑦1, 𝑦2, . . . , 𝑦𝑛 si 𝜆 numere reale.Analog echipam Z𝑛

2 cu o adunare vectoriala definita de adunarea binara pecomponente si o inmultire cu scalari (0 sau 1). De exemplu in Z3

2 avem:

(1, 0, 1) ⊕ (1, 1, 0) = (0, 1, 1)

0 ⊙ (1, 0, 1) = (0, 0, 0)

2

Echipata cu aceste operatii multimea Z𝑛2 devine un spatiu vectorial peste

corpul K = Z2 si putem discuta despre liniar independenta, sisteme de genera-tori, subspatii, dimensiune. Spre deosebire de R𝑛 spatiul vectorial Z𝑛

2 contineun numar finit de 2𝑛 vectori.

Codul Hamming (7, 4): pentru doua numere intregi 𝑘 ≤ 𝑛, un subspatiuvectorial alui a Z𝑛

2 de dimensiune 𝑘 se numeste cod liniar (𝑛, 𝑘).Consideram matricea 𝐻 cu elemente in Z2 a carei coloane notate 𝑐1, 𝑐2, . . . , 𝑐7

sunt formate din cei 7 vectori nenuli din Z3:

𝐻 =

⎛⎜⎜⎜⎝0 0 0 1 1 1 1

0 1 1 0 0 1 1

1 0 1 0 1 0 1

⎞⎟⎟⎟⎠Subspatiul liniar:

𝑘𝑒𝑟 𝐻 :=

⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎩

⎛⎜⎜⎜⎜⎜⎜⎝𝑥1

𝑥2

...

𝑥7

⎞⎟⎟⎟⎟⎟⎟⎠ ∈ Z72 : 𝐻

⎛⎜⎜⎜⎜⎜⎜⎝𝑥1

𝑥2

...

𝑥7

⎞⎟⎟⎟⎟⎟⎟⎠ =

⎛⎜⎜⎜⎜⎜⎜⎝0

0...

0

⎞⎟⎟⎟⎟⎟⎟⎠

⎫⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎭poarta numele de codul Hamming (7, 4)

Se poate arata ca:

𝐵 = {(1, 0, 0, 0, 0, 1, 1), (0, 1, 0, 0, 1, 0, 1), (0, 0, 1, 0, 1, 1, 0), (0, 0, 0, 1, 1, 1, 1)}

formeaza o baza a spatiului vectorial 𝑘𝑒𝑟 𝐻.Matricea G ale carei linii sunt elementele bazei 𝐵 se numeste matricea

generatoare a codului Hamming (7,4):

𝐺 :=

⎛⎜⎜⎜⎜⎜⎜⎝1 0 0 0 0 1 1

0 1 0 0 1 0 1

0 0 1 0 1 1 0

0 0 0 1 1 1 1

⎞⎟⎟⎟⎟⎟⎟⎠Mai jos explicam procedura codului Hamming si corectarea erorilor dar pen-

tru aceasta trebuie sa facem urmatoarele remarci. Fie {𝑒1, 𝑒2, . . . , 𝑒7} bazacanonica in Z7

2. Putem verifica relatiile 𝐻𝑒𝑖 = 𝑐𝑖 pentru orice 𝑖 = 1, 7 si prinurmare niciunul dintre vectorii bazei canonice nu se afla in 𝑘𝑒𝑟 𝐻.

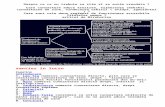
1. Daca 𝑣 apartine lui 𝑘𝑒𝑟 𝐻 atunci 𝑣 + 𝑒𝑖 nu apartin lui 𝑘𝑒𝑟 𝐻 pentruorice 𝑖.

2. Daca 𝑣 este un vector din Z72 pentru care exista un 𝑖 astfel ca 𝐻𝑣 = 𝑐𝑖

atunci 𝑣 + 𝑒𝑖 apartine lui 𝑘𝑒𝑟 𝐻 si pentru 𝑗 = 𝑖 avem ca 𝑣 + 𝑒𝑗 nu apartinacestei multimi.

Algoritmul pentru corectarea erorilor cu codul (7,4)

3

Sa presupunem ca vrem sa transmitem un cuvant u constand din patru cifrebinare 𝑢1, 𝑢2, 𝑢3, 𝑢4, si presupunem ca acesta ar putea fi deformat de interferentecare ii schimba doar o componenta. Fie 𝑤 cuvantul primit.

1. Pentru a coda u, formam combinatia liniara 𝑣 a elementelor din baza 𝐵de mai sus cu cele patru componente a lui u ca si coeficienti. De fapt 𝑣poate fi obtinut din cuvantul original prin inmultirea cu matricea 𝐺:

𝑣 =(𝑢1 𝑢2 𝑢3 𝑢4

)𝐺

Prin constructie vectorul 𝑣 apartine lui 𝑘𝑒𝑟 𝐻. De remarcat ca rezultatul

calculului(𝑢1 𝑢2 𝑢3 𝑢4

)𝐺 este un vector cu sapte componente ale

carui prime patru componente reprezinta mesajul original.

2. Se calculeaza 𝐻𝑤, unde 𝐻 este matricea descrisa mai sus.

3. Daca 𝐻𝑤 = 0, atunci 𝑤 partine lui 𝑘𝑒𝑟 𝐻. Astfel, prezenta unei singureerori va insemna ca w nu apartine lui 𝑘𝑒𝑟 𝐻. In acest caz concluzionam canu au existat deformari si u este reprezentat de primele patru componenteale lui w.

4. Daca 𝐻𝑤 = 𝑐𝑖 pentru un anumit 𝑖, atunci 𝑣 + 𝑒𝑖 este un vector din 𝑘𝑒𝑟 𝐻iar 𝑣 + 𝑒𝑗 nu apartine lui 𝑘𝑒𝑟 𝐻 pentru 𝑗 = 𝑖. In acest caz schimbamcomponenta a i-a in 𝑤 (de le 0 la 1 sau de la 1 la 0) si obtinem un nouvector ��. Primele sale patru componente vor fi acum reprezentate decuvantul u

In tehnica de mai sus cuvintele trimise sunt foarte scurte: doar 4 componente.In realitate mesajele electronice contin mult mai multe componente si decodareanu poate fi facuta decat cu ajutorul calculatorului, calculele fiind enorme. Oproblema cu codul Hamming (7,4) este ca nu poate detecta mai mult de o eroare.

Puteti exersa cele prezentate mai sus:Am receptionat mesajul 𝑤 = 1100011 criptat cu ajutorul codului Hamming

(4, 7). Stim ca s-a scurs cel mult o eroare in transmisia sa. Aflati mesajuloriginal.

4

Notiuni teoretice:

∙ un spatiu vectorial (𝑉,⊕,⊙,K) peste corpul (K,+, ·) este reprezentat decatre o multime 𝑉 ale carei elemente se numesc vectori (putem sa ni-i imaginamca fiind niste imagini) pe care am definit o operatie de adunare ⊕ (simpla lipirea imaginilor) si de scalare ⊙ (marire-micsorare a imaginilor). Operatiile maisus amintite trebuie sa satisfaca urmatoarele axiome:

𝐴1: Nu conteaza ordinea in care lipim imaginile, obtinem aceeasi panorama

��⊕ (𝑣 ⊕ ��) = (��⊕ 𝑣) ⊕ ��

𝐴2: Exista o imagine nula care prin lipire nu schimba nimic

∃ 0, 𝑣 ⊕ 0 = 0 ⊕ 𝑣 = 𝑣

𝐴3: Exista o imagine inversa care prin lipire anuleaza totul

∀𝑣, ∃(−𝑣), 𝑣 ⊕ (−𝑣) = (−𝑣) ⊕ 𝑣 = 0

𝑆1: Daca scalam imaginea 𝛽% si apoi 𝛼% este ca si cum am scala (𝛼 · 𝛽)%

𝛼⊙ (𝛽 ⊙ 𝑣) = (𝛼 · 𝛽) ⊙ 𝑣

𝑆2: Daca scalam 𝛼% doua imagini lipite este ca si cum am lipi intai imaginilescalate 𝛼% anterior

𝛼⊙ (��⊕ 𝑣) = (𝛼⊙ ��) ⊕ (𝛼⊙ 𝑣)

𝑆3: Putem lipi imagini scalate diferit dupa regula

(𝛼⊙ 𝑣) ⊕ (𝛽 ⊙ 𝑣) = (𝛼 + 𝛽) ⊙ 𝑣

𝑆4: O scalare 100% nu modifica imaginea

1 ⊙ 𝑣 = 𝑣

5

∙ un sistem de vectori 𝑆 = {𝑣1, 𝑣2, . . . , 𝑣𝑝} ai unui spatiu vectorial se numesteliniar independent daca:

𝜆1𝑣1 + 𝜆2𝑣2 + . . . + 𝜆𝑝𝑣𝑝 = 𝜃 =⇒ 𝜆1 = 𝜆2 = . . . = 𝜆𝑝 = 0.

Practic 𝑆 este un sistem liniar independent daca niciun vector din 𝑆 nu se poateexprima ca o combinatie liniara de vectori din 𝑆.

Mod practic de studiu al liniar independentei:Fie (𝑉,⊕,⊙,K) un spatiu vectorial si 𝐵𝑐 = {𝑒1, 𝑒2, . . . , 𝑒𝑛} o baza canonica

a sa. Pentru stabilirea liniar independentei unui sistem de 𝑝 vectori:

𝑆 = {𝑣1, 𝑣2, . . . , 𝑣𝑝}

se exprima fiecare dintre acestia in functie de vectorii bazei 𝐵𝑐. Matricea formatacu coeficientii (scalarii) acestor reprezentari o notam cu 𝐴. Daca:

rang(𝐴) = numar de vectori ai sistemului S = 𝑝

atunci 𝑆 este liniar independent.Remarca: O baza canonica a spatiului IR3 este:

𝑒1 = (1, 0, 0), 𝑒2 = (0, 1, 0), 𝑒3 = (0, 0, 1)

O baza canonica a spatiului IR2[𝑋] este:

𝑒1 = 𝑋2, 𝑒2 = 𝑋, 𝑒3 = 1.

O baza canonica a spatiului 𝑀2(IR) este:

𝐸1 =

⎛⎝1 0

0 0

⎞⎠ , 𝐸2 =

⎛⎝0 1

0 0

⎞⎠ , 𝐸3 =

⎛⎝0 0

1 0

⎞⎠ , 𝐸4 =

⎛⎝0 0

0 1

⎞⎠∙ un sistem de vectori 𝑆 = {𝑣1, 𝑣2, . . . , 𝑣𝑝} se numeste sistem de gener-

atori a spatiului vectorial 𝑉 daca pentru orice vector 𝑣 ∈ 𝑉 exista scalarii𝜆1, 𝜆2, . . . , 𝜆𝑝 ∈ K astfel ca:

𝑣 = 𝜆1𝑣1 + 𝜆2𝑣2 + . . . + 𝜆𝑝𝑣𝑝.

Adica orice vector al spatiului se poate exprima ca o combinatie liniara a vec-torilor sistemului 𝑆.

Mod practic de studiu al sistemelor de generatori:Fie (𝑉,⊕,⊙,K) un spatiu vectorial si 𝐵𝑐 = {𝑒1, 𝑒2, . . . , 𝑒𝑛} o baza canonica

a sa. Pentru a stabili daca un sistem de 𝑝 vectori:

𝑆 = {𝑣1, 𝑣2, . . . , 𝑣𝑝}

este un sistem de generatori a lui 𝑉 se exprima fiecare dintre acestia in functie devectorii bazei 𝐵𝑐. Matricea formata cu coeficientii (scalarii) acestor reprezentario notam cu 𝐴. Daca:

rang(𝐴) = dimensiunea spatiului vectorial V = 𝑛

atunci 𝑆 este sistem de generatori.

6

∙ Baza a spatiului vectorial= sistem liniar independent+sistem de generatori∙ daca relativ la o baza 𝐵 = {𝑒1, 𝑒2, . . . , 𝑒𝑛} avem scrierea:

𝑣 = 𝛼1𝑒1 + 𝛼2𝑒2 + . . . + 𝛼𝑛𝑒𝑛

numim 𝛼1, 𝛼2, . . . , 𝛼𝑛 coordonate ale vectorului 𝑣 relativ la baza 𝐵 si notam:

[𝑣]𝐵 =

⎛⎜⎜⎜⎜⎜⎜⎝𝛼1

𝛼2

...

𝛼𝑛

⎞⎟⎟⎟⎟⎟⎟⎠ .

∙ daca 𝐵1 = {𝑒1, 𝑒2, . . . , 𝑒𝑛} si 𝐵2 = {𝑒′1, 𝑒′2, . . . , 𝑒′𝑛} sunt baze in (𝑉,+, ·,K)si ⎧⎪⎪⎪⎨⎪⎪⎪⎩

𝑒′1 = 𝑎11𝑒1 + 𝑎21𝑒2 + . . . + 𝑎𝑛1𝑒𝑛

𝑒′1 = 𝑎12𝑒1 + 𝑎22𝑒2 + . . . + 𝑎𝑛2𝑒𝑛

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

𝑒′𝑛 = 𝑎1𝑛𝑒1 + 𝑎2𝑛𝑒2 + . . . + 𝑎𝑛𝑛𝑒𝑛

se numeste matricea de trecere de la baza 𝐵1 la baza 𝐵2 matricea:

𝑇𝐵1𝐵2=

⎛⎜⎜⎜⎜⎜⎜⎝𝑎11 𝑎12 . . . 𝑎1𝑛

𝑎21 𝑎22 . . . 𝑎2𝑛...

... . . ....

𝑎𝑝1 𝑎𝑝2 . . . 𝑎𝑝𝑛

⎞⎟⎟⎟⎟⎟⎟⎠∙ daca 𝑇𝐵1𝐵2

este matricea de trecere de la baza 𝐵1 la baza 𝐵2 atunci auloc relatiile:

𝑇𝐵1𝐵2 = 𝑇−1𝐵2𝐵1

𝑇𝐵1𝐵2= 𝑇𝐵1𝐵 · 𝑇𝐵𝐵2

si:[𝑣]𝐵2

= 𝑇−1𝐵1𝐵2

· [𝑣]𝐵1.

7

Probleme rezolvate

Problema 1.

Solutie:

Problema 2.

Solutie:

Problema 3.

Solutie:

Problema 4.

Solutie:

Problema 5.

Solutie:

Problema 6.

Problema 7.

8

Probleme propuse

Problema 1. In matematica de liceu apare de multe ori rationamentul numit”identificarea coeficientilor”. De fiecare data in spatele scenei sta ascuns unspatiu vectorial:

In multimea numerelor complexe stim ca:

𝑎 + 𝑏𝑖 = 𝑐 + 𝑑𝑖 ⇐⇒ 𝑎 = 𝑐, 𝑏 = 𝑑

Deci am identicat coeficientii.

i) Arati ca 𝑉 = C impreuna cu adunarea si inmultirea cu scalari din K = Ceste un spatiu vectorial si 𝐵 = {1, 𝑖} este o baza a acestuia.

Doua polinoame de grad trei 𝑝 = 𝑎1𝑋2 + 𝑏1𝑋 + 𝑐1 si 𝑞 = 𝑎2𝑋

2 + 𝑏2𝑋 + 𝑐2 suntegale ⇐⇒ 𝑎1 = 𝑎2, 𝑏1 = 𝑏2 si 𝑐1 = 𝑐2

ii) Arati ca 𝑉 = {𝑎𝑋2 + 𝑏𝑋 + 𝑐 : 𝑎, 𝑏, 𝑐 ∈ R} impreuna cu adunarea poli-noamelor si inmultirea cu scalari din K = R este un spatiu vectorial si𝐵 = {1, 𝑋,𝑋2} este o baza a acestuia.

Doua matrice de ordin doi 𝐴 =

⎛⎝𝑎 𝑏

𝑐 𝑑

⎞⎠ si 𝐵 =

⎛⎝𝑥 𝑦

𝑧 𝑡

⎞⎠ sunt egale ⇐⇒

𝑎 = 𝑥, 𝑏 = 𝑦, 𝑐 = 𝑧 si 𝑑 = 𝑡.

iii) Care este spatiul vectorial care permite aceasta identificare ? Cum aratao baza a sa ? Putem sa interpretam matricele ca pe niste vectori multi-dimensionali ?

Problema 2. Aratati ca multimea:

𝑉 = {(𝑥, 𝑦, 𝑧, 𝑡) ∈ R4 : 2𝑥− 3𝑦 + 𝑧 − 𝑡 = 0}

impreuna cu adunarea si inmultirea cu scalari obisnuite din R4 formeaza unspatiu vectorial.

Problema 3. Sa se studieze daca urmatoarele sisteme de vectori sunt liniarindependente. In caz contrar, sa se determine un subsistem 𝑆′ maximal liniarindependent, precum si dependenta liniara a acestora:

a) 𝑆 = {𝑝1 = −𝑋2+7𝑋+8, 𝑝2 = −𝑋2+3𝑋+2, 𝑝3 = 𝑋2−𝑋+1} ⊂ IR2[𝑋].b) 𝑆 = {𝑣1 = (1, 1,−1), 𝑣2 = (1.0, 2), 𝑣3 = (0, 1, 3)} ⊂ IR3

Problema 4. Sa se studieze care din sistemele de vectori date sunt sisteme degeneratori pentru spatiile mentionate:

a) 𝑆 = {𝑝1 = 𝑋2 + 𝑋 + 1, 𝑝2 = 𝑋2 + 𝑋, 𝑝3 = 𝑋2} ⊂ IR2[𝑋]

b) 𝑆 =

⎧⎨⎩𝐴1 =

⎛⎝1

1

⎞⎠ , 𝐴2 =

⎛⎝1

2

⎞⎠ , 𝐴3 =

⎛⎝0

1

⎞⎠⎫⎬⎭ ⊂ 𝑀2,1(IR)

c) 𝑆 = {𝑣1 = (𝑖, 0, 𝑖), 𝑣2 = (0,−𝑖, 0), 𝑣3 = (2𝑖,−𝑖, 2𝑖)} ⊂ lC3.

9

Problema 5. Fie sistemele de vectori:

𝐵1 = {𝑓1 = (1, 1, 0), 𝑓2 = (1, 0, 0), 𝑓3 = (1, 1, 2)}

𝐵2 = {𝑔1 = (1, 1, 3), 𝑔2 = (1, 1, 2), 𝑔3 = (3, 2, 4)}.

a) Aratati ca 𝐵1 si 𝐵2 sunt baze ale spatiului vectorial IR3

b) Aflati matricea de trecere 𝑇𝐵1𝐵2

c) Sa se determine coordonatele vectorului 𝑣 relativ la baza 𝐵1 daca acestaeste dat prin 𝑣 = −2𝑔1 + 𝑔2 + 3𝑔3.

Problema 6. Fie baza 𝐵 = {𝑣1 = (2, 1), 𝑣2 = (3, 2)} ⊂ IR2. Se cere:

a) Sa se determine baza 𝐵1 ⊂ IR2 stiind ca 𝑇𝐵𝐵1 =

⎛⎝1 1

5 6

⎞⎠a) Sa se determine baza 𝐵2 ⊂ IR2 stiind ca 𝑇𝐵2𝐵 =

⎛⎝1 2

4 9

⎞⎠

Problema 7. Sa se arate ca vectorii 𝑣1 = (1,−1,−1), 𝑣2 = (1,−1, 0) si 𝑣3 =(1, 0, 0) formeaza o baza pentru IR3 si sa se determine coordonatele vectorului𝑢 = (1, 2, 3) in aceasta baza.

10