193 8. PLCIISTRUCTURIDINPLCI 8.1. Generaliti Oplacesteuncorpsolidcareareunadintredimensiuni (grosimea)maimicdectcelelaltedouipoatefiprivitca materializareauneisuprafee,aacumobarestematerializarea unei linii. O plac se definete, n general, prin forma i dimensiunile suprafeeimediane,iarnfiecarepunctalacesteia,seconsidero normalpecaresedefinetegrosimea,h,deoparteidealtaa suprafeei mediane, prin valorile h/2. Plcile au o importan deosebit n ingineria mecanic, deoarece numeroasestructuriauncomponenalorplcideofoartemare varietatedeformeidimensiuni.Estecazulechipamentelor energetice,chimice,siderurgice,almainilorunelteidelucru, vehiculelor auto, navale i feroviare, al unor cupole i acoperiuri etc. Structurile mecanice se realizeaz prin asamblarea diverselor plci componente prin sudur, turnare,nituire etc, sauprin combinaiiale acestor procedee. Calculul plcilor istructurilor din plcieste dificil, deoarece se ajungelasistemedeecuaiicuderivatepariale,greudeintegrat. Chiarpentruproblemerelativsimplevolumulcalculelorestefoarte mare.Deasemenea,trebuiefcutcalculstatic,dinamic,devibraii, de stabilitate etc. Chiar la nceputurile teoriei elasticitii i rezistenei materialelor s-aajunslaconcluziacpentruplcitrebuieelaboratoteorie proprie, deoarece nu este posibil utilizarea ecuaiilor generale (5.10) aleteorieielasticitii(dinnousepoatefaceoparalelcubarele). Teoria plcilor face o serie de ipoteze simplificatoare, unele generale, de principiu i altele de calcul, prin care se neglijeaz unii termeni dinecuaiilesausoluiilerespective.Dinacestemotives-aajunsn situaiadefaptcseutilizeazmaimultevariantealeteoriei 194 plcilor,fiecareavnddelimitrile,precizia,avantajelei dezavantajele sale. ncercriledeaelaboraoteoriegeneralaplciloraufost abandonatedatoritdificultilordecalcul.Prinurmare,nprezent, dinconsiderentepractice,sefolosescninginerieteoriidistincte pentru, cel puin, urmtoarele categorii de plci: - plci subiri (cu grosime mic), cu deformaii i deplasri mici; - plci subiri, cu deplasri mari; - plci groase. Deasemenea,s-auelaboratteoriiirelaiidecalculpentru plcilecurbeipentruceleplane,care,larndullor,sempartn plciderotaie(ngeneral),cilindrice,sferice,conice,toroidaleetc, respectivplciplanedreptunghiulare,circulareetc.Oplacplan poatefiprivitcauncazparticularaluneiplcicurbeianumeo plac curb cu curbur nul. Conceptuldegrosimemicsaumareaplcii,determin posibilitile de neglijare a unor termeni din ecuaiile sau relaiilede calculpentruplcilesubiri.Placsubireseconsiderceapentru care grosimea este relativ mic n comparaie cu raza de curbur sau cu dimensiunile plcii i anume:-dacplacaestecurb,raportuldintregrosimeahirazade curbur principal R trebuie s satisfac condiia h/R < 1020; -dacplacaesteplan,raportuldintregrosimeahilungimea (sau limea plcii) trebuie s satisfac condiia h/ < 1020. Deplasareawaplciipedirecianormaleilasuprafaamedian se consider mic, dacw/h < 510, iar placa se consider cu deplasri mici.ncadrulcategoriilormenionate,deobicei,seconsiderc plcilesuntelastice,calcululnregimelasto-plasticdesolicitare fiind foarte dificil. S-auimpus,deasemenea,teoriiirelaiidecalculdistincte pentru plci plane i pentru plci curbe (nveliuri), deoarece exist o diferenesenialnprivinaefectuluisarcinilorexterioareasupra plcilor curbe, comparativ cu cele plane:1. Echilibrulstatical unui element de plac plan,ncrcat cu o sarcintransversal,esteposibilnumaidatoritapariiei 195 momentelorncovoietoareidersucire,nsoite,deobiceiide fore tietoare. 2.Oplaccurb,ngeneral,transmitesarcinileexterioarectre reazemeprinsolicitriledemembran,careacioneazparalelcu planultangentlasuprafaamedianaplci,dinpunctulconsiderat, tensiunile (normale, , de ntindere sau compresiune) fiind constante pegrosime,studiulacesteiproblemefcndobiectulteorieide membranaplcilor.Aceastproprietateaplcilorcurbesubirile face,deregul,sfiemultmairigideimaieficientedectplcile plane,naceleaicondiiidesolicitare,derezemareidematerial (aspecteletehnologicenusecomenteazaici).nprincipiu, solicitriledemembransuntindependentededeformaiileproduse desolicitriledencovoiere,rsucireiforfecare(cndacesteasunt mici). Reaciunileideplasrileobinutecuteoriademembrann zoneledemarginesunt,deregul,incompatibilecucondiiilereale de pe frontier (contur, margine), motiv pentru care, trebuie avut n vedereincovoiereanacestezone,care,ngeneral,areefecte locale. Pentrustudiultensiunilornvecintateasarcinilorconcentrate aplicateplcilor,trebuiefolositeteoriispeciale,specifice problemelor spaiale ale teoriei elasticitii. Calcululstructurilordinplcisepoatefacenumaicuajutorul calculatoarelor,fiepentrucazuriparticulare,cacelalstructurilor axialsimetrice(derotaie),pentrucares-auelaboratalgoritmii programeadecvate,fie,ncazulgeneral,cumetodenumerice,ca metodaelementelorfinite,metodadiferenelorfinitesaumetoda elementelor de frontier. Dinconsiderentedidactice,ncontinuare,sevorprezentadoar ctevaprobleme(relativsimple)aleplcilorsubiri,elastice,cu deplasri mici. Ipotezelecareseaunvederenteoriaplcilorsubiri,elastice, cu deplasri mici sunt urmtoarele: - suprafaa median a plcii este inextensibil, adic n ea nu se producdeformaiidentinderesaucompresiune:suprafaamedian 196 rmneneutrlancovoiereaplci,ceeaceserealizeazdac suprafaa este desfurabil; - o normal rectilinie la suprafaa median, nedeformat a plcii, rmnerectilinieinormallasuprafaamedian,deformat,a plcii; - tensiunile normale , pe direcia normalei la suprafaa median a plcii sunt mici i se neglijeaz. Deasemenea,sefaceprecizareac,pentruplci,eforturilese definesc pe unitatea de lungime n planul median, adic forele axiale iceletietoareauunitiledemsurN/mm,iarmomentele Nm/mm, sau variante ale acestora. 8.2. Plci curbe subiri elastice O plac curb subire este definit de o suprafa median curb. Dupformasuprafeeimediane,plcileseclasificnplcicu curbur simpl i plci cu dubl curbur. n geometria diferenial a suprafeelorsedemonstreazcexisttotdeaunadouseciuni realizatecuplanecareconinnormala,perpendicularentreele,n carerazeledecurburauvaloriextreme,1i2.Curburile corespunztore,ceamaxim,1/1,respectiv,1/2,minim,se numesc curburile principale ale plcii. Razadecurbur,,ntr-unplancarefaceunghiulcuplanul principal I (relaia lui Euler), este:2212sin cos 1 + =.(8.1) n geometriasuprafeelor (in teoria plcilor curbe) sefolosesc i mrimile: -curbura total sau curbura lui Gauss:K=1/12; (8.2) -curbura medie:H = 1/1 + 1/2 . (8.3) abc Figura 8.1 197 Cnd curbura lui Gauss este pozitiv (K>0),curburile principale auacelaisemn,suprafaaesteconvexisenumetesinclastic (elipsoidul, sfera, paraboloidul de rotaie), ca n figura 8.1.a, iar cnd K0.ntr-unpunctsituatladistanazdesuprafaamedianstareade tensiuni este definit de componentele x, y, xy = yx i xz, yz (v. fig. 8.2.a). Se observ c arcele situate la distana z de suprafaa median au lungimile dx+(z/x)dx, respectiv dy +(z/y)dy. Efortul circumferenial Nx este:}+||.|

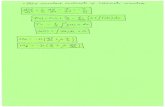
\|+ o =2 h2 hyx xdz dyzdy dy N, 198 care se simplific cu dy, deoarece nu variaz cu z i rezult relaia de echivalen mecanic dintre tensiunea x i efortul Nx }+||.|

\|+ o =2 h2 hyx xdzz1 N .Analog, se obine i efortul axial}+||.|

\|+ o =2 h2 hxy ydzz1 N .(8.1.a) Procednd asemntor rezult i expresiile pentru celelalte eforturi: - eforturile tangeniale }+||.|

\|+ t =2 h2 hyxy xydzz1 T ;}+||.|

\|+ t =2 h2 hxyx yxdzz1 T ; (8.1.b) - eforturile de forfecare }+||.|

\|+ t =2 h2 hyxz xdzz1 T ;}+||.|

\|+ t =2 h2 hxyz ydzz1 T ; (8.1.c) - momentele ncovoietoare }+||.|

\|+ o =2 h2 hyx xdzz1 z M ; }+||.|

\|+ o =2 h2 hxy ydzz1 z M ; (8.1.d) ab Figura 8.2 199 - momentele de rsucire }+||.|

\|+ t =2 h2 hyxy xydzz1 z M ;}+||.|

\|+ t =2 h2 hxyx yxdzz1 z M .(8.1.e) nfigura8.2.bs-aureprezentateforturiledefiniteprinrelaiile (8.1), momentele fiind reprezentate prin sgei duble.Observaii:1.Conformprincipiuluidualitiitensiunilortangenialexy= yx, dar, avnd n vedere c, n general, x y, rezult c (a se vedea relaiile (8.1.b) i (8.1.e))pentrueforturiletangenialeipentruceledersucireprincipiuldualitii nu mai este valabil, adicTxy Tyxi Mxy Myx.(8.2) 2.Notaiileisensurile(pozitive)aletensiunilorieforturilordinfigura8.2 sunt cele mai des utilizate, dar se folosesc, de diveri autori i diverse variante ale acestora.3.Relaiile(8.1)semainumescirelaiiledeechivalenmecanicdintre tensiuni i eforturi.Pentrudeterminareatensiunilorntr-unpunctalplciitrebuie determinatecelezeceeforturidinrelaiile(8.1),darnusunt disponibiledectaseecuaiideechilibru,adicproblemaestede patruoristaticnedeterminat.Celepatruecuaiisuplimentare necesare se pot obine prin studiul deformaiilor elementului de plac avut n vedere. Dac grosimeah a plciieste relativmicn raport cu razele de curbur x i y, se pot neglija rapoartele z/x i z/y n relaiile (8.1) i expresiile celor zece eforturi devin: } }++o = o =2 h2 hy y2 h2 hx x; dz N ; dz N} } }+++t = t = t = =2 h2 hyz y2 h2 hxz x2 h2 hxy yx xy; dz T ; dz T ; dz T T (8.3) } } }+++o = = o = o =2 h2 hxy yx xy2 h2 hy y2 h2 hx xdz z M M ; dz z M ; dz z M .Numrul eforturilor necunoscute a sczut la opt. Pentru sistemul spaialdeforeimomentedinfigura8.2.bsepotscrieaseecuaii 200 deechilibrumecanic.Trebuie,deci,ssescriedouecuaiide deformaii. Rigiditatea la ncovoiere a plcii. Caurmareaipotezelorenunate,ntr-oplacsubire,solicitat numailancovoiere,stareadetensiuniesteplan(s-afcutipoteza c z = 0), deci- deformaiile specifice sunt: x = (x y) / Ei x = (x y) / E;(8.4.a)- tensiunile normale sunt: ). (1 E), (1 Ex z2y y x2xc v + cv = o c v + cv = o (8.4.b) Seconsideroseciunea plcii n planul Oxz, ca n figura 8.3iseaunvederepunctele AiP,naintecaplacasse deformeze(punctulPseaflla distanazfadesuprafaa medianaplcii).Dup deformareaplciipunctele ajungnA,respectivP. DeplasareauapunctuluiPeste u -zx, n care x = dw/dx, este panta tangenteidusn punctul A la suprafaa deformat, adic u -z dw/dx. (8.5.a) Procednd asemntor i n planul Oyz, se obine v -z dw/dy. (8.5.b) Se scriu succesiv:-deformaiile specifice: x= du / dx = -z d2w/dx2; y= dv / dy = -z d2w/dy2; -tensiunile:||.|

\|v +v = o||.|

\|v +v = o22222x22222xdxw ddyw d1E z,dyw ddxw d1E z. (8.6) Momentelencovoietoaresecalculeazcurelaiile(8.3) corespunztoare: Figura 8.3 201 ||.|

\|v +v =||.|

\|v +v = o = } }++222223 2 h2 h2 h2 h222222x xdyw ddxw d) 1 ( 12Ehdzdyw ddxw d1E zdz z M , n care se noteaz rigiditatea la ncovoiere a plcii:D = Eh3 / [12(1-2)],(8.7) formafinalaexpresiilorcelordoumomentencovoietoare,n funcie de deplasri fiind:||.|

\|v + =||.|

\|v + =2222y2222xdxw ddyw dD M ,dyw ddxw dD M . (8.8) Starea de echilibru de membran. Pentrunumeroaseproblemeingineretisepotaccepta urmtoarele ipoteze simplificatoare: - tensiunile x, y, xy = yx sunt constante pe grosimea plcii; - tensiunile xz i yz sunt nule (sau neglijabile). nacestcazparticularsunttreieforturinecunoscute:Nx,Nyi Nxy=Nyx, ca n figura 8.4, pentru care se pot scrie doar trei ecuaii de echilibru, pentru fore (pe direcia normalei la suprafaa median ipe dou direcii din planul tangent), ecuaiile de momente fiind identic satisfcute. Stareadesolicitareauneiplcicurbe, caracterizatnumaiprineforturileNx,Nyi Nxy=Nyx,senumetestaredeechilibrude membran.Plcilecurbeaflatentr-oastfel destaredesolicitaresunt,ngeneral,static determinate,deoarecenumruleforturilor este egal cu cel al ecuaiilor de echilibru care se pot scrie, adic, eforturile pot fi determinate doar din ecuaiile de echilibru, condiii de deformare a plcii ne fiind necesare. Observaii: 1. Starea de solicitare de membran ntr-o plac curb nu se poaterealizapentruoricecondiiidencrcareirezemare.Deexemplu, pentru o sarcin concentrat, cel puinn zona din vecintatea punctului de aplicaie, trebuie s se in seama de efectele de ncovoiere, deoarece ele nu pot fi neglijate. 2.Rezemareaplciitrebuiessefacastfelnctreaciuniles acioneze n planul tangent la suprafaa median. n general aceast condiie estegreudendeplinitdincauzadeformaiilorplciisaudincauza Figura 8.4 202 deplasrilor reazemului. Prin urmare, foarte frecvent n zonele de rezemare aparsolicitridencovoierelocale,valorilelorsczndfoarterepedela distane relativ mici de reazem. 8.3.Metodologiageneraldeanalizaplcilorsubiri elastice Pentruastabiliecuaiilediferenialealeplcilor(curbesau plane)deregul,primeletreietapemetodologicesuntaceleaicu celecares-auprezentatn5.1,intitulatSistemuldeecuaiial teoriei elasticitii i anume: 1.Sescriuecuaiiledeechilibrupentruelementuldeplac considerat,subaciuneaeforturilor(v.fig.8.2.b)iauneisarcini aplicat n centrul elementului, acesta reprezentnd aspectul mecanic alproblemei.Pentruaceastatrebuiessefacipotezeasupra tensiunilor care se au n vedere i a eforturilor corespunztoare.2.Sescriurelaiilentredeplasriideformaiispecifice, denumiteirelaiidecompatibilitategeometric,carereprezent aspectulgeometricalproblemei.Aceastaeste,deregul,etapacea mai dificila demersului. Pentru scrierea acestor relaii se consider modulncaresedeformeazplaca,sealegcomponentele deplasrilorcareurmeazsseconsiderencalculicaresunt deformaiile specifice pe care le produc. 3.Sescriurelaiiledintretensiuniideformaiilespecifice (lege lui Hooke), ceea ce reprezint aspectul fizic al problemei. 4. Se fac diverse operaii de calculasupra ecuaiilor obinute, cu scopul de ale aducelaformemai simple, de exemplu: seneglijeaz uniitermeni,sefacnlocuirialeunorexpresiinaltele,cuscopul eliminrii unora dintre necunoscute etc. n final se ajunge la una sau mai multe ecuaii difereniale n care, cel mai frecvent, necunoscutele sunt componente ale deplasrilor unuipunct alsuprafeeimediane a plcii, adic ecuaiile obinute sunt scrise n funcie de deplasri i potfiomogenesauneomogene,linearesaunelineare,cusaufr derivate pariale. 5.Seintegreazecuaiadiferenial(sausistemul)ise determinosoluieparticularaecuaieineomogene(daceste cazul). Soluiile pot fi nchise, pentru probleme mai simple, sau pot fideformaunordezvoltrinserie,cuunnumroarecarede 203 termeni,pentruproblememaicomplicate,cazncareprecizia soluiei depinde de numrul termenilor luai n calcul. Metodeledecalculfolositepentruintegrareaecuaiilorplcilor suntdeomarediverse:analitice,cufunciidevariabilecomplexe, numericeetc.Soluiilegsiteconinunnumrdeconstantede integrare, pentru aflarea crora se pot utiliza alte metode de calcul: a colocaiei, a celor mai mici ptrate etc. 6.Pentrucalcululuneiplcidatetrebuiescrisecondiiilela limit i derezemare, pentru determinarea constantelor deintegrare, ale cror valori se nlocuiesc n soluia ecuaiei. 7.Relaiiledecalculobinutepermitdeterminareavalorilor deplasriloritensiunilornpuncteledeinteresaleplcii.n numeroasesituaiistareadetensiunidinplacestespaial,ceeace implicutilizareauneiteoriidestarelimit,pentruaverificadac placa rezist n bune condiii. Chiarpentruproblemerelativsimplevolumulcalculeloreste considerabil,motivpentrucare,nprezent,plcileistructuriledin plci se calculeaz cu metode i programe adecvate, pe calculator. 8.4.Plcicurbesubiriderotaie,nstaredesolicitareide echilibru de membran Plcilecurbederotaiesedefinescprinsuprafeemediane generate prin rotirea unei curbe plane, C, denumit meridian, n jurul unei drepte, , din planul ei, care este axa plcii, ca n figura 8.5. Figura 8.5 Un punct A de pe curb descrie uncerc de raz r, denumitcerc paralel. Fie raza de curbur, 1= O1A, n punctul A. A doua seciune principalesteperpendicularpeprimaiconinenormaladin 204 punctulA.Razaeidecurburseobineprinaplicareateoremeilui Meusnier i are valoarea O2A = 2 = r sin . Caoconsecinasimetriei,poziiaunuipunctpesuprafaa median a plcii este foarte simplu de definit prin dou unghiuri (fig. 8.6.a): - unghiul dintre axa de rotaie i normala la suprafa; - unghiul dintre un plan meridian oarecare i planul meridian de referin, de exemplu, cel care trece prin punctul A. Pentruadeterminaeforturiledinplacacurbconsiderat,se defineteunpatrulatercurbiliniu,infinitmicABCD,canfigura 8.6.a, cu laturile: AD = BC = 1d, AB = r di CD = [r + (dr/d) d]. Pesuprafeelelateralealeelementuluiacioneazeforturilede membran reprezentate n figura 8.6.b. De asemenea, s-a considerat i o sarcin distribuit, p, cu componentele px , py i pz. Eforturile se consider pozitive cnd: ab Figura 8.6 - N i N - produc solicitri de ntindere; -TiT-ausensurileinverseaceloradecreterea unghiurilor i . Pentruforelecareacioneazasupraelementuluideplacdin figura 8.6.b se scriu trei ecuaii de echilibru. 1. Ecuaia de proiecie pe direcia tangentei la cercul paralel, Ox, (fig. 8.6.b i 8.7) duce la o relaie stufoas,care se simplificfoarte mult dup ce se fac urmtoarele operaii: - sin d/2 d/2 i cos d/2 1; - se neglijeaz infiniii mici de ordin superior; 205 - se are n vedere c d = cos - ecuaia se mparte cu d.d. Figura 8.7 Forma final a ecuaiei este: 0 p r cos TTrrTNx 1 1 1= + + cc+ cc+u ccuuuu. (8.9) 2. Ecuaia de proiecie pe direcia tangentei la meridian, Oy, (fig. 8.6.bi8.8)seobineprocedndasemntorcapentruecuaia(8.9) i rezult: 0 p r cos NT NrrNy 1 1 1= + u cc + cc+ ccuu .(8.10) Figura 8.8Figura 8.9 3. Ecuaia de proiecie pe direcia normalei la suprafaa median, Oz,(fig.8.6.bi8.9)seobine,procedndasemntorcapentru ecuaiile (8.9) i (8.10) i rezult: z2 1pNN=+u, (8.11.a) 206 sau, prin mprirea cu grosimea h (avnd n vedere c tensiunile sunt constante pe grosime), se obine ecuaia lui Laplace hpz2 1=o+ou. (8.11.b) Observaie:nfigurile8.7,8.8i8.9s-aureprezentatnumaieforturilecare intervin n ecuaia la care se refer fiecare figur.Relaiile (8.9), (8.10) i (8.11) constituie un sistem de trei ecuaii avndcanecunoscutefunciileN,NiT=Teforturilede membrandinplac.Seobservcrelaia(8.11)nueste diferenial, ceea ce permite eliminarea unuia dintre eforturile N sau Niastfelsistemuldeecuaiirmasaredouecuaiicudou necunoscute.Integrareaacestuisistemdeecuaiieste,ngeneral, dificil.ncazuriparticulare,ca,deexemplu,pentruplcicu ncrcaresimetricfadeaxaderotaie,ecuaiilesesimplifici integrarea lor devine posibil. 8.5. Plci cilindrice subiri Se consider o plac cilindric (cu seciune inelar), cu raza, r, a suprafeei mediane, grosimea, h, constant, ncrcat cu o sarcin, p, simetric distribuit n raport cu axa cilindrului (o presiune). nplacs-adefinitunelementinfinitmic,canfigura8.10, pentru care se vor scrie ecuaiile de echilibru. Figura 8.10 Datorit simetriei axiale, eforturile din plac sunt: - forele tietore de membran Tx=Tx i momentele de rsucireMx=Mx sunt nule; 207 -forelenormaleNimomentelencovoietoareMsunt constante de-a lungul circumferinei. nacestecondiiisepotscrienumaitreiecuaiideechilibru pentru eforturile care acioneaz asupra plcii: - proiecia forelor dup direcia x 0 d dx rdxdNx= ; (8.12) - proiecia forelor dup direcia z 0 d dx r p d dx N d dx rdxdTx= + + ; (8.13) - suma momentelor dup direcia y 0 d dx r T d dx rdxdMxx= . (8.14) Din relaia (8.12) rezult c efortul axialNx este constant. Se va considera c Nx = 0. n cazul n care exist efort axial, deformaiile i tensiunileprodusedeacestasepotcalculafoartesimpluise nsumeaz cu celelalte.Ecuaiile (8.13) i (8.14) se simplific i devin p Nr1dxdTx = + i0 TdxdMxx= ,(8.15) pentru integrarea crora trebuie avut n vedere i modul de deformare al plcii. Deformaiile specifice sunt (fig. 8.10): dxdux = c i rwd rd r d ) w r ( = = c.(8.16) Caurmareasimetrieiaxiale,deplasareavndirecie circumferenial este nul. Cu legea lui Hooke se determin tensiunile ,dxdurw) 1 (E) () 1 (E;rwdxdu) 1 (E) () 1 (E2x22x2x|.|

\|v + v = c v + cv = o|.|

\|v v = c v + cv = o (8.17) care permit calculul eforturilor, cu relaiile (8.3), avndnvedere c tensiunile sunt constante pe grosimea, h, a plcii: 208 |.|

\|v + v =|.|

\|v v =dxdurw) 1 ( EhN ;rwdxdu) 1 (h EN2 2x.(8.18) Aplicnd condiiaNx = 0 primei relaii (8.18), se obinedu/dx = w/r,care, nlocuit n a doua dintre relaiile (8.18) duce la rezultatul N = - Ehw / r.(8.19) Din relaiile (8.15) se elimin fora tietore Tx i se obine ecuaia p wrh EdxM d2 2x2 = . (8.20) Datoritsimetrieiaxiale,deplasareawesteconstantndirecie circumferenial, adic dw/d=0 irelaiile (8.8) devin:x2222xMdxw dD M ,dxw dD M v = v = =. (8.21) n aceste condiii ecuaia (8.20) devinep wrh EdxM dD2 4x4= + ,(8.22) care capt o form mai simpl dac se introduce notaia2 2224h r) 1 ( 3D r 4 h E v = = | (8.23) i anumeDpw 4dxw d444= | + , (8.24) ncareDesterigiditatealancovoiereaplciidefinitprinrelaia (8.7). Soluia general a ecuaiei (8.24) estew=ex(C1cosx+C2sinx)+e-x(C3cosx+C4sinx)+f(x),(8.25) n care f (x) este o soluie particular a ecuaiei neomogene (8.25), iar C1,,C4 sunt constante de integrare, care se determin din condiiile delaceledoucapetealecilindrului(pentrux=0ix=), considerat de lungime . Aceste condiii pot avea n vedere: - deplasrile: sgeata radial w i rotirea normalei dw/dx; -eforturile:momentelencovoietoare,MiM,carese calculeaz cu relaiile (8.21); fora tietore, care se determin din cea de a doua relaie (8.15) i anume Tx=dMx/dx i fora circumferenial N= -Ehw/r din relaia (8.19). 209 8.6. Plci plane subiri Seconsideroplacplan,dreptunghiular,degrosime constant, h, solicitat cusarcini transversalei orizontale, raportat la sistemule de coordonate Oxyz, ca n figura 8.11. Marepartedinprocedurilei relaiiledecalculprezentate rmnvalabile,avndnvedere coplacplanesteuncaz particularaluneiplcicurbe:are curburile zero (razele de curbur infinite). Sereiaurelaiile(8.6)aletensiunilorscrisenfunciede deplasri,caresecompleteazcutensiuniletangeniale,avndn vedere (8.5) i xy xy2xy) 1 ( 2 E;y xwz 2yuxvv += tc cc =cc+cc= . Forma complet a relaiilor (8.6) este: Figura 8.12 .y xw1E z,xwyw1E z,ywxw1E z2xy22222x22222xc ccv += t||.|

\|ccv +ccv = o||.|

\|ccv +ccv = o (8.26) Din observarea relaiilor (8.26) se constat c tensiunile x, y i xy variaz linear pe grosimea plcii, aa cum se vede n figura 8.12. ncazulgeneraldesolicitareaplciimaiexistitensiuni tangenialexzi yz,paralelecudireciaOz,normallasuprafaa median,canfigura8.2.a.Pentrudeterminareaacestortensiunise folosescrelaiiledeechilibruCauchy(5.1),frsarcinimasice,din care se obine: ||.|

\|c cc+ccv =||.|

\|ct c+co c =ct c||.|

\|c cc+ccv =||.|

\|ct c+co c =ct cy x wyw1 zEx y z,y x wxw1 zEy x z23332yx y yz23332xyx xz.(8.27) Ecuaiile (8.27) se integreaz n raport cu z i rezult: Figura 8.11 210 ) y , x (2zy x wyw1 E, ) y , x (2zy x wxw1 E2223332yz1223332xz +||.|

\|c cc+ccv = t +||.|

\|c cc+ccv = t,(8.28) ncare 1(x,y) i 2(x,y) suntfuncii arbitrare, care se determin din condiiacatensiuniletangenialexzi yz saibvalorinulepe suprafeele plcii, adic pentru z = h/2 i se obine: .y x wyw) 1 ( 8h E) y , x (,y x wxw) 1 ( 8h E) y , x (23332222333221||.|

\|c cc+ccv = ||.|

\|c cc+ccv = (8.29) Se nlocuiesc expresiile (8.29) n (8.28) |.|

\|||.|

\|c cc+ccv = t|.|

\|||.|

\|c cc+ccv = t2z8hy x wyw1 E,2z8hy x wxw1 E2 223332yz2 223332xz(8.30) irezultctensiunilexzi yz variazparabolicpegrosimeaplcii, canfigura8.13(lafelcancazul barelor drepte). Sedetaeazdinplacun elementparalelipipedic,culaturile dx, dy i h, ca n figura 8.14, ncrcat cu o sarcin uniform distribuit p. Se are n vedere, pe feele laterale, o fie de nlime dz, pe care acioneaz tensiunile tangenialexz i

yz, dup direcia Oz (fig. 8.14).Celelaltetensiuninuse menioneaz, nefiind implicate n demersul care urmeaz. Ecuaiadeechilibrua forelor,ndireciaOz,care acioneazasupraelementului considerat(dupefectuarea reducerilorisimplificrilor) Figura 8.13 Figura 8.14 211 este:p dzy x2 h2 hyzxz=||.|

\|ct c+ct c}+. (8.31) Se introduc relaiile (8.30) n ecuaia (8.31) i se are n vedere c integrareasefacenumainraportcuz.Dupefectuareacalculelor rezult succesiv:p dz2z8hywy x w2xw1 E2 h2 h2 2442 24442= |.|

\|||.|

\|cc+c cc+ccv }+ i (8.32.a) Dpywy x w2xw442 2444=cc+c cc+cc,n care D este rigiditatea la ncovoiere a plcii (8.7). Ecuaia (8.32) este cunoscut cu numele ecuaia Sophie Germain aplcilorplane.Eaareoformmaisimpldacsefolosete operatorul lui Laplace2222y x cc+cc= Ai ecuaia devine Dpw = AA . (8.32.b) Expresiileeforturilordinplac,nfunciededeplasareaw,se obinnlocuindvaloriletensiunilor(8.26)i(8.30)nrelaiile(8.3); calculele sunt simple, deoareceintegralele se calculeazn raport cu z i deci: n calculul plcilor sunt adeseori utile relaiile difereniale dintre eforturiisarcini.Pentruastabiliastfelderelaii,pentruplcile planes-aconsideratunelementparalelipipedic,culaturiledx,dyi h,canfigura8.15,ncrcatcuosarcinuniformdistribuitp, (8.33) ||.|

\|c cc+cc =||.|

\|c cc+cc =y x wywD T ;y x wxwD T2333y2333x. ;y xwD ) 1 ( M;xwywD M ;ywxwD M2xy2222y2222xc ccv =||.|

\|ccv +cc =||.|

\|ccv +cc = 212 pentrucaresescriuecuaiiledeechilibru(momenteles-aufigurat cu sgei duble), care, dup reduceri i simplificri, duc la relaiile: Figura 8.15 - ecuaia de proiecie a forelor pe direcia Oz pyTxTyx =cc+cc;(8.34) - ecuaia de momente n raport cu Ox yxy yTxMyM=cc+cc;(8.35) - ecuaia de momente n raport cu Oy xyxxTyMxM=cc+cc. (8.36) Dacseeliminforeletietoaredinrelaiile(8.34),(8.35)i (8.36) se obine: pyMy xM2xM2y2xy22x2 =cc+c cc+cc. (8.37) Deoarecesoluiageneralaecuaieidifereniale(8.32)este foarte dificil de obinut, s-au elaborat metode deintegrare a ecuaiei pentru diverse cazuri particulare, care au importan inginereasc, cel mai important fiind cazul plcilor dreptunghiulare. 8.7. Plci plane subiri dreptunghiulare Soluiaecuaiei(8.32),esteofunciew(x,y),caretrebuies verificeecuaiaw=p/Dicondiiilelalimit.Pentruplcile dreptunghiulare, cea mai utilizat metod de calcul este cea a seriilor 213 Fourier duble, cnd sarcina variaz dup ambele variabile x i y i a seriilor Fourier simple, cnd sarcina este funcie doar de o variabil. Se presupunec placa are dimensiunilea ib. Sarcina p(x,y) se dezvolt n serie Fourier sub forma | o =m nn m mny sin x sin a ) y , x ( p ,(8.38) n care s-au folosit notaiile m = m / a i n = n / b. Se presupune c deplasarea w(x,y) poate fi scris sub forma: | o =m nn m mny sin x sin A ) y , x ( w , (8.39) Amn fiind constante de integrare. Dacplacaestesimplurezematpecelepatrulaturialesale,se verific faptul c soluia (8.39) satisface condiiile: - pentru x = 0 i x = a, w = 0 ix = Mx = 2w / dx2 = 0,- pentru y = 0 i y = b, w = 0 iy = My = 2w / dy2 = 0. Soluiacutat(8.39)trebuiessatisfacecuaiaw=p/Da plcii, deci nlocuind funcia w(x,y) se obine: | o = | o | + | o + om nn m mnm nn m mn4n2n2m4my sin x sin aD1y sin x sin A ) 2 (Dinidentificareacoeficienilortermenilorsinmxsinny rezult: 2 2n2mmnmn) ( DA| + oo= , (8.40) iar deplasarea w este: | o| + oo=m nn m2 2n2mmny sin x sin) ( D) y , x ( w .(8.41) Exemplu. Pentru o plac dreptunghiular, simplu rezemat pe toate laturile, ncrcat cu sarcina uniform distribuit p, se obine amn=16p/2mn i =| + o| ot=m ,.. 5 , 3 , 1 n2 2n2mn m2) ( mny sin x sinDp 16) y , x ( w . (8.42) Sgeatamaximestelamijloculplcii(x=a/2,y=b/2)iare valoarea: = +| + ot=m ,.. 5 , 3 , 1 n2 2n2m1 2 / ) n m (2max) ( mn ) 1 (Dp 16w .(8.43) 214 8.8. Plci plane subiri circulare O alt categorie de plci subiricare prezintinterespractic este celalplcilorcirculare,studiereaacestorafiindmaiconvenabiln coordonate polare, ceea ce implic urmtoarele transformri: - operatorul lui Laplace devine 222 22r1r r1r u cc+cc+cc= A ;(8.44) - ecuaia (8.32) va avea forma: Dp wr1rwr1rwr1r r1r222 22222 22=||.|

\|u cc+cc+cc||.|

\|u cc+cc+cc.(8.45) PentrudeterminarearelaiilordelegturdintreeforturileMx, My, i Mxy, definite n raport cu coordonatelecartezieneOxyiMr, M, Mr,definite nraport cu coordonatele polare Or,sescriu Figura 8.16 ecuaiiledeechilibrupentruunelementdeplaccuformaunei prisme triunghiulare, ca n figura 8.16 i se obin urmtoarele relaii: Mr = Mx cos2 + My sin2 - 2Mxy sin cos; M = Mx sin2 + My cos2 + 2Mxy sin cos;(8.46) Mr = (Mx - My)sin cos + Mxy(cos2 - sin2). Princalculesimple,utilizndrelaiileobinuteanterior,seobin expresiile eforturilor n funcie de deplasarea w: ;wr1rwr1rwD M222 22r(((

||.|

\|u cc+ccv +cc = ;w wr1rwr1D M22222((

u ccv +u cc+cc =u

.wr1rD ) 1 ( Mr||.|

\|u ccccv =u(8.47) 215 .wr1rwr1rwr1D T;wr1rwr1rwrD T222 22222 22r||.|

\|u cc+cc+ccu cc =||.|

\|u cc+cc+cccc =u(8.48) Dacncrcareaplciiesteaxialsimetric,toatederivatele parialenraportcuvariabilasuntnuleirelaiiledemaisusse simplificiarecuaiacuderivatepariale(8.45)devineecuaia ordinar Dpdrdwr1drw dr1drw dr2drw dsau,Dpdrdwr1drw ddrdr1drd3 222 33442222= + += |.|

\|+ |.|

\|+.(8.49) Ecuaia(8.49)estelinear,detipEuler,neomogen,acrei soluie este w = C1 + C2 r2 + C3 ln r + C4 r2 ln r + w*, (8.50) n care w* este o soluie particular a ecuaiei neomogene. Pentru cazurile n care sarcina p este un polinom n r, de forma==n0 kkkr ADp,(8.51) sencearcsoluiiparticularedetipulbiriiseobinesoluia particular =++ +=n0 k4 k2 2 k*r) 4 k ( ) 2 k (Aw .(8.52) De asemenea i expresiile (8.47) i (8.48) ale eforturilor se simplific i devin . 0 T ;drdwr1drw ddrdD T; 0 M ;drw ddrdwr1D M ;drdwr1drw dD M22rr2222r= |.|

\|+ == |.|

\|v + = |.|

\|v + =uu u (8.53) Condiiilelalimitpentruplcilecirculare(inelare),ncrcate simetric, se scriu astfel pentru: - margine ncastrat: w = 0 i dw/dr = 0; - margine rezemat: w = 0 i Mr = 0; - margine liber: Mr = 0 i Tr = 0; 216 - pentru plcile circulare pline (fr orificii centrale), pentru r = 0 (ncentrulplcii),deplasareawimomentulncovoietorMr trebuie s aib valori finite, ceea ce implic absena din expresiile respective a termenilor care conin log r i duce la C3 = 0 i C4 = 0. Exemplu. Pentru o plac circular, ncastrat pe contur, ncrcat cu sarcin uniform distribuit p, se scriu succesiv relaiile: - deplasarea: w = C1 + C2 r2 + C3 ln r + C4 r2 ln r + pr4/64D; - rotirea: dw/dr = 2C2 r + C3/r + C4(2r ln r +r) + pr3/16D. Condiia can centrul plcii (pentru r =0) w i Mr s aibvalori finite duce la rezultatele C3= C4=0, iar relaiile anterioare devin: - deplasarea: w = C1 + C2 r2 + pr4/64D; - rotirea: dw/dr = 2C2 r + pr3/16D. Condiiilepeconturulexterior,ncastrat,alplciisunt:w= dw/dr = 0, pentru r = R i se obine: C1 + C2 R2 + pR4/64D = 0;2C2 R + pR3/16D = 0din care rezult:C1 = pR4/64D ;C2 = - pR2/32D. nlocuindacestevalorinexpresiileanterioare,seobinrelaiile de calcul pentru placa considerat: .2prT ;Rr) 3 1 ( ) 1 (16pRM ;Rr) 3 ( ) 1 (16pRM;D 32) r R ( pdrdw;D 64) r R ( pD 64prD 32pRD 64pRwr22 222 2r2 2 2 2 2 4 2 4 =((

v + v + =((

v + v + = == + =u 8.9. Structuri din plci Numeroasestructurimecanicesuntrealizatedintablecarese asambleaz,deregul,prinsudur.Avantajelepracticealeacestor tipuridestructuridecurgdinfaptulcpotaveaformeorictde complicate,suntrelativuoare,iartehnologiiledefabricaiesunt ieftine i foarte bine puse la punct, cu un nalt grad de mecanizare i automatizare.Calcululacestorechipamente,maini,instalaii,vehiculeetc trebuiefcutpemodeledestructuridinplci.Avndnvedere complexitateaformelor geometrice ale acestor structuri i exigenele calculului care poate fi de rezisten, rigiditate, stabilitate, dinamic 217 etcseimpuneutilizareaunoralgoritmi,metodeiprogramede calcul generale i utilizareacalculatoarelor. Deci calculul se face fie,ncazulgeneral,cumetode numericegenerale,ca metodaelementelorfinite, metoda diferenelor finite sau metodaelementelorde frontier(v.cap9),fie, pentrucazuriparticulare,ca celalstructuriloraxial simetrice(derotaie),cu algoritmiiprograme adecvate. Unexempluilustrativ, este prezentat n figura (8.17), pentru un utilaj siderurgic, care a fost modelat i calculat cu metoda elementelor finite.Programelecuelementefiniteoferutilizatorilorzecidetipuri deelementefinitepentruplci,pentruaseputeaelabora,cuele, modeledecalculcaressatisfaccelemaidiverseexigene inginereti. Pentruocategoriemai restrns de structuri din plci i anumeacelorderotaie(axial simetrice),s-auelaborat algoritmicaredescompun structurancomponentesimple, pentru care se cunosc relaiile de calcul,ca,deexemplu,plci planecirculare,plcicilindrice, conice, sferice, toroidale etc. Apoi,pecontururilede asamblarealecomponentelor, caresuntnitecercuri,sescriu condiiiledeegalitateale deplasrilorideechilibruale eforturilor, care duc la obinerea unui sistem de ecuaii din carese determinconstantele deintegrare Figura 8.17 Figura 8.18 218 dinsoluiilecomponentelorstructurii.Odatcunoscutevalorile constantelordeintegrare,nfiecarecomponentastructuriisepot calcula, n oricare punct al su, deplasrile, tensiunile, eforturile etc.nfigura8.18seprezint,caexemplu,unbuncrcareafost realizat din 9 componente i anume: - 4 plci inelare (componentele 1, 5, 6, 9); - 3 plci cilindrice (componentele 2, 4, 8); - 2 plci conice (componentele 3, 7). Numrul circumferinelor de legtur (de asamblare) este 6. Fiecaredincele9componentealestructuriiareosoluiecare conine4constantedeintegrare,decintotal4*9=36necunoscute. Pentru fiecare din cele 6 circumferine se scriu urmtoarele ecuaii: -condiiideegalitate(continuitate)adeplasrilorradialew,ale componentelor conectate pe conturul respectiv; -condiiideegalitatearotirilornormalelorlasuprafeele mediane ale componentelor conectate pe conturul respectiv; -condiiadeechilibru(sumasfiezero)amomenteloraxiale, pentru componentele conectate pe conturul respectiv; -condiiadeechilibru(sumasfiezero)aforelorpedirecie radial, pentru componentele conectate pe conturul respectiv. Bibliografie 1.Constantinescu,I.N.,Tacu,T.,Calculederezistenpentru utilajetehnologice,Structuriizotrope,axialsimetrice,Editura tehnic, Bucureti, 1979. 2.Constantinescu,I.N.,Picu,C.,Hadr,A.,Gheorghiu,H., Rezistenamaterialelorpentruingineriamecanic,EdituraBREN, Bucureti, 2006. 3.Timoshenko,S.,Woinowsky-Krieger,S.,Teoriaplcilor plane i curbe, Editura tehnic, Bucureti, 1968.4.Voinea,R.,Voiculescu,D.,Simion,F.P.,Introduceren mecanicasoliduluicuaplicaiininginerie,EdituraAcademiei, Bucureti, 1989.