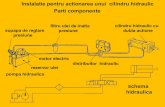
Manual Hidraulica -Hidrotehnica
-
Upload
adnana1972 -
Category
Documents
-
view
218 -
download
20
Transcript of Manual Hidraulica -Hidrotehnica

Francisc Grudnicki Ioan Ciornei
HIDRALULICA LUCRĂRILOR
PENTRU
CORECTAREA TORENŢILOR
2007

1
C U P R I N S PREFAŢĂ 1.NOŢIUNI GENERALE. 1.1.Fluide.Definiţii.Clasificare. 1.1.1.Lichide reale 1.1.2.Lichide perfecte 1.2.Modele folosite în hidraulică 1.2.1.Modelul mediului continuu 1.2.2.Alte modele 1.3.Proprietăţile fizice ale lichidelor 1.3.1.Densitatea 1.3.2.Greutatea specifică 1.3.3.Compresibilitatea 1.3.4.Vâscozitatea 1.4.Forţele care acţionează asupra lichidelor 1.4.1.Foţele masice exterioare 1.4.2.Forţele masice interioare 1.4.3.Forţele de contact exterioare 1.4.4 Forţele de contact interioare 1.4.5.Presiunea.Forţa de presiune 1.4.6.Unităţile de măsură ale presiunii 2.STATICA LICHIDELOR 2.1.Echilibrul hidrostatic. 2.1.1.Ecuaţiile lui Euler. 2.1.2.Ecuaţia generală diferenţială a hidrostaticii 2.1.3.Potenţial. Suprafeţe echipotenţiale 2.1.3.1.Funcţia de forţă. Poteţial 2.1.3.2.Suprafeţe echipotenţiale.Proprietăţi. 2.2.Legea hidrostaticii în câmpul gravitaţional terestru. 2.2.1.Ecuaţia fundamentală a hidrostaicii 2.2.2.Interpretarea ecuaţiei fundamentale. 2.3.Forţe de presiune pe suprafeţe plane 2.3.1.Forţe de presiune.Centre de presiune. 2.3.1.1.Mărime forţei de presiune hidrostatică 2.3.1.2.Centrul de presiune. 2.3.1.3.Componentele forţei de presiune 2.3.2.Forţe de presiune pe suprafeţe dereptunghiulare 2.3.2.1.Forţe de presiune pe suprafeţe plane verticale 2.3.2.2.Forţe de presiune pe suprafeţe plane oblice 2.3.2.3.Forţe de presiune pe suprafeţe combinate. 2.3.3.Paradoxul hidrostatic. 2.3.4.Curba integrală a presiunii 2.3.4.1.Definiţie. 2.3.4.2.Aplicaţie 2.4.Forţe de presiune pe suprafeţe curbe deschise 2.4.1.Mărimea forţei de presiune 2.4.2.Coordonatele centrului de presiune 2.4.3 Aplicaţie.

2
2.5. Plutirea corpurilor 2.5.1.Legea lui Arhimede 2.5.2.Condiţia de plutire 2.5.3.Pescajul plutitorilor cilindrici 2.6.Forţa de presiune a apei cu aluviuni 2.6.1.Presiunea hidrostatică a apei cu aluviuni 2.6.2.Forţa de presiune a apei cu aluviuni 2.7. Echilibrul relativ 2.7.1.Definiţia echilbrului relativ 2.7.2.Supraînălţarea apei în curba canalelor 3.DINAMICA LICHIDELOR 3.1.Elementele mişcării lichidelor 3.1.1.Noţiuni fundamentale 3.1.2.Clasificarea mişcării lichidelor. 3.1.2.1.Criterii de clasificare 3.1.2.2.Mişcări permanente şi mişcări nepermanente 3.1.2.3.Mişcări tridimensionale,bidimensionale şi unidimensionale
3.1.2.4.Alte tipuri de mişcări 3.1.3.Sisteme de reprezentare a mişcării lichidelor 3.1.3.1.Sistemul de reprezentare Lagrange 3.1.3.2.Sistemul de reprezentare Euler 3.2.Ecuaţiile de mişcare a lichidelor perfecte 3.2.1.Parametrii mişcării lichidelor perfecte 3.2.2.Echilibrul hidrodinamic.Ecuaţiile lui Euler 3.2.3.Ecuaţia de echilibru 3.2.4.Ecuaţia de continuitate 3.2.5.Ecuaţia generală a mişcării permanente 3.2.6.Ecuaţia lui Daniel Bernoulli 3.2.6.1.Ecuaţia lui Beroulli în mişcarea permanentă a lichidelor perfecte
3.2.6.2.Reprezentarea grafică ţi interpretarea ecuaţiei lui Bernoulli 3.2.6.3.Ecuaţia lui Bernoulli în mişcarea permanentă a lichidelor incompresibile reale
3.2.6.4.Coeficientul lui Coriolis 3.2.6.5.Ecuaţia lui Bernoulli pentru curent de lichid real cu suprafaţă liberă
3.2.6.6.Panta hidraulică,piezometrică,geodezică. 3.2.6.7.Pierderea de sarcină în mişcarea permanentă 3.2.6.8.Bilanţul energetic în mişcarea permanentă 3.2.6.9.Ecuaţia lui Bernoulli pentru cuurent curbat în plan vertical 3.2.6.10.Presiunea de impact 3.2.7.Teorema impulsului. 4.SCURGEREA PERMANENTĂ ÎN ALBII DESCHISE 4.1.Generalităţi 4.1.1.Definiţie 4.1.2.Clasificarea albiilor deschise. 4.2.Parametrii miişcării permamnente uniforme în albii 4.2.1.Parametrii geometrici ai albiei.

3
4.2.2 Distribuţia presiunilor. 4.2.3.Viteza curentului 4.2.3.1.Formula lui Chézy pentru viteza medie 4.3.2.2.Coeficientul de viteză C 4.2.3.3.Reparţiţia vitezelor în sceţiune transversal 4.2.4.Debitul.Modulul de viteză şi de debit 4.2.5.Pierderile de sarcină 4.2.6.Efortul tangenţial la perete 4.3.Studiul energetic al curenţilor cu suprafaţă liberă 4.3.1.Energii specifice 4.3.2.Mişcări lente şi mişcări rapide 4.3.3 Alte criterii de recunoaştere a regimului de mişcare. 4.3.3.1.Criteriul lui Froude 4.3.3.2.Criteriul adâncimii.Adâncimea critică. 4.3.3.3.Criteriul vitezei.Vioteza critică 4.3.3.4.Criteriul pantei.Panta critică 4.4.Mişcarea permanentă gradual variată 4.4.1.Generalităţi 4.4.2.Secţiunea de comandă 4.4.3.Ecuaţia generală diferenţială a mişcării permanente gradual variate 4.4.4.Forma şi calculul curbelor suprafeţelor libere 4.4.4.1.Forma curbelor suparfeţelor libere 4.4.4.2.Calculul curbelor suprafeţelor libere 4.4.5.Saltul hidraulic 4.4.5.1.Definiţia saltului hidraulic.Forme. 4.4.5.2.Elementele saltului hidraulic 4.4.6.Scurgerea torenţială. 4.4.6.1. Consideraţiuni generale 4.4.6.2. Caracteristicile hidraulice ale scurgerii torenţiale 5.HIDRAULICA CONSTRUCŢIILOR PENTRU CORECTAREA TORENŢILOR 5.1.Generalitaţi. 5.2.Orificii.Ajutaje.Barbacane 5.2.1.Definiţii.Clasificare 5.2.2.1.Definiţii 5.2.2.2.Clasificarea orificiilor 5.2.2.Secţiunea contractată 5.2.3.Orificii mici în regim permanent 5.2.3.1.Viteza 5.2.3.2.Debitul volumic 5.2.3.3.Determinarea teoretică a coeficientului de contracţie 5.2.4.Orificii mari în regim permanent 5.2.4.1.Orificii mari liberi 5.2.4.2.Orificii cu muchii ascuţite înecate în aval 5.2.5.Orificii şi ajutaje 5.2.6.Barabacane în regim permanent 5.3.Deversoare 5.3.1.Definţii 5.3.2.Clasificarea deversoarelor 5.3.3.Deditul deversoarelor cu prag subţire 5.3.3.1.Deversorul dreptunghiular.formula generală pentru debitul prin deversor

4
5.3.3.2.Deversorul triunghiular 5.3.3.3.Deversorul trapezoidal 5.3.4.Deditul deversoarelor cu prag gros 5.3.5.Dimensionarea deversoarelor 5.4.Disipatoare hidraulice de energie 5.4.1.Afuierea barajelor 5.4.2.Definiţii.Părţi componente 5.4.3.Tipuri de disipatoare 5.4.3.1.Disipatoare cu prag transversal pe radier 5.4.3.2.Disipatoare cu trepte de cădere 5.4.3.3.Radier cu dinţi disipatori de energie. 5.4.3.4.Alte tipuri de disipatoare de energie. 5.4.4.Dimensionarea disipatoarelor de energie 5.4.4.1.Parametrii principali 5.4.4.2.Lungimea de bătaie a lamei deversante 5.4.4.3.Adâncimea contractată 5.4.4.4.Dimensiunile radierului 5.4.4.5.Dimensiunile dinţilor disipatori 5.4.4.6.Înălţimea zidurilor de gardă 5.5.Confuzoare 5.5.1.Definţii.Condiţii de racordare 5.5.2.Lungimea confuzorului 5.5.3.Inălţimea zidului de gardă 5.6.Canale 5.6.1.Definiţii.Condiţii hidraulice şi constructive. 5.6.2.Canale cu secţiuni optime din punct de vedere hidraulic 5.6.3.Dimensionarea canalelor 5.6.3.1 Condiţii hidraulice şi de stabilitate 5.6.3.2.Parametrii principali de calcul 5.6.3.3.Stabilitatea canalelor la eroziune 5.6.3.4.Calculul canalelor 5.7.Evazoare

1
P R E F A Ţ Ă
Pluviomodelarea reliefului, ca efect al scurgerii apelor meteorice, pe versanţi şi albii. face parte din hidromorfogeneză, ca proces de contact, cu caracteristici specifice din punct de vedere hidrologic, geomorfologic şi hidraulic.
Bazinele hidrografice, în conceptul de sisteme cibernetice deschise, sunt receptoare de imputuri de de autputuri de materie şi energie.
In condiţii de transfer dezechilibrat de materie şi energie, pluviomodelarea reliefului, ca proces şi efecte, capătă forme specifice “ torenţiale”.
Efectele torenţializării bazinelor hidrografice sunt deosebit de nefaste, atât pe plan ecologic, cât şi pe plan socio-economic.
Complexul lucrărilor de amenejare a bazinelor hidrografice torenţiale, denumit şi corectarea torenţilor, cuprinde o categorie de lucrări deosebit de importantă, şi anume cea a lucrărilor hidrotehnice pe versanţi şi în special în reţeaua hidrografică.
Prevenirea torenţializării bazinelor hidrografice, combaterea şi atenuarea efectelor torenţializării, implică studii şi analize foarte aprofundate privind geneza şi evoluţia proceselor torenţiale, care sunt specifice fiecărui torent.
Stabilirea soluţiilor optime, în cadrul complexului de lucrări pentru corectarea torenţilor, proiectarea, executarea şi asigurarea mentenabilităţii lucrărilor hidrotehnice, presupune cunoştinţe multidisciplinare, printre care în primul rând, cele de hidraulică.
În acest context, lucrarea cuprinde cinci capitole: Noţiuni generale, în care se definesc: lichidele; modelele de studiu folosite în hidraulică;
proprietăţile fizice ale lichidelor; forţele care care acţionează asupra lichidelor. Statica lichidelor, în care se tratează: echilibrul hidrostatic cu ecuaţiile aferente;
potenţialul şi suprafeţele echipotenţiale;legea hidrostaticii în câmpul gravitaţional terestru; relaţiile pentru cuantificarea forţelor de presiune hidrostatică pe suprafeţe plane şi curbe,care acţionează asupra lucrărilor hidrotehnice; plutirea corpurilor; echilbrul relativ.
Dinamica lichidelor, cuprinde: elementele mişcării lichidelor; mişcarea lichidelor cu ecuaţiile lui Euler şi Bernoulli; pierderea de sarcină şi bilanţul energetic în mişcarea permanentă; cuantificarea presiunii de impact şi a forţei de impact.
Scurgerea permanentă în albii deschise, în care sunt expuse relaţiile pentru: cuantificarea parametrilor geometrici ai albiilor; cuantificarea parametrilor hidraulici ai scurgerii (presiune, viteză, debit, efort tangenţial la perete); energia curenţilor cu suprafaţă liberă; mişcarea gradual varaiată şi caracteristicile scurgerii torenţiale.
Hidraulica construcţiilor pentru corectarea torenţilor, capitol în care sunt redate relaţiile pentru dimensionarea orificiilor, barbacanelor, deversoarelor şi disipatoarele de energie ale barajelor; dimensionarea lucrărilor hidrotenice longitudinale de pe reţeaua hidrografică a bazinelor cum sunt confuzoarele, canalele, evazoarele.
Lucrarea se adresează studenţilor şi absolvenţilor facultăţilor de silvicultură, cât şi tuturor celor care au preocupări în domeniul corectării torenţilor, protejării mediului şi a reconstrucţiei ecologice în bazinele hidrografice torenţiale.
Autorii

1
1. N O Ţ I U N I G EN E R A L E .
Hidraulica ca parte a Mecanicii fluidelor, studiază echilibrul şi mişcarea lichidelor şi
interacţiunea acestora cu corpurile solide. 1.1. FLUIDE. DEFINIŢII. CLASIFICARE.
Fluidele sunt corpuri materiale, cu forţe de coeziune între particule foarte mici, care
sub acţiunea gravitaţiei, iau forma recipientelor în care sunt conţinute. Fluidele se prezintă sub două stări: -lichidă: apa, alcoolul, petrolul, uleiurile, mercurul, materialele topite. -gazoasă:aerul, vaporii, diverse gaze. Fluidele pot suporta numai compresiuni. Lichidele sunt practic incompresibile, au un volum determinat, la condiţii identice de
presiune şi trmperatură, şi formează o suprafaţă liberă ce le delimitează de atmosferă. Lichidele se clasifică în două categorii: lichide reale şi lichide perfecte (ideale). 1.1.1. LICHIDE REALE. Lichidele reale sunt lichidele aşa cum se găsesc în natură. Caracteristica principală a
acestora este vâscozitatea, de unde şi denumirea lor de lichide vâscoase. Schimbarea formei lor se face numai cu consum de energie, necesară învingerii tensiunilor tangenţiale interioare.
Sub aspectul vâscozităţii lichidele se împart în: -lichide puţin vâscoase: apa, alcoolul, benzina, etc. -lichide vâscoase: apa de canal, apa cu nămol, uleiurile, glicerina. -lichide foarte vâscoase: mercurul, asfaltul topit, metalul topit. 1.1.2. LICHIDE PERFECTE. Lichidele perfecte (ideale), care nu există în natură, sunt lichidele lipsite de
vâscozitate. Modificarea formei acestora se efectuiază fără consum de energie, neexistând tensiunile tangenţiale din interior. Rezultă că asupra unui corp în mişcare în interiorul unui lichide perfect acţionează numai forţe normale.
Lichidele perfecte se caracterizează prin următoarele caracteristici fizice: perfectă fluiditate, omogenitate, izotropie, incompresibilitate, nedeformabilitate, la variaţiile de temperatură.
1.2. MODELE FOLOSITE ÎN HIDRAULICĂ. 1.2.1.MODELUL MEDIULUI CONTINUU. Prin model de fluid se înţelege o schemă simplifcată de fluid, căruia îi sunt atribuite
principalele proprietăţi macroscopice ale fluidului real. Fluidele, ca şi întreaga materie, au o structură discontinuă. Mecanica Fluidelor, studiază
mişcarea fluidelor, din punct de vedere macroscopic, făcând abstracţie de structura moleculară discontinuă. În consecinţă fluidul este considerat mediu continuu, format din particule de fluid care umplu complet şi compact, fără goluri, volumul luat în considerare.
Particula de fluid este un volum ekementar de fluid, indivizibil, omogen şi deformabil, ce conţine un număr considerabil de molecule, şi este mic în raport cu volumul de fluid, dar mare în raport cu distanţele dintre molecule.

Deci particula de fluid nu este identică cu molecula de fluid, şi poate fi oricât de mare până la limita impusă de aplicarea calculului diferenţial.
Forma particulei de fluid poate fi oarecare (tetraedrică, paralelipipedică, sferică, cilindrică, etc.) funcţie de fenomenul studiat.
Rezultă că lichidele sunt considerate medii continue deformabile. 1.2.2. ALTE MODELE. Pe lângă modelul continuu, sunt acceptate în funcţie de fenomenele şi condiţiile în care
se produc, şi următoarele modele: -Modelul Newton al fluidului vâscos (real). -Modelul Pascal al fluidului incompresibil. -Modelul Euler al fluidului perfect (ideal). -Modele spaţiale unidimensionale, bidimensionale şi tridimensionale. 1.3. PROPRIETĂŢILE FIZICE ALE LICHIDELOR. Principalele proprietăţi fizice ale lichidelor utile sunt: densitatea, greutatea specifică,
compresibilitatea, vâscozitatea. 1.3.1. DENSITATEA. Densitatea (masa specifică, masa unităţii de volum) a unui lichid omogen este
mărimea scalară dată de raportul dintre masa (m) şi volumul lichidului considerat (V):
Vm
=ρ (1.1)
Densitatea lichidului variază cu presiunea şi temperatura. Această variaţie fiind mică, în tehnică se adoptă în mod curent valori constante pentru densitate.
Apa distilată la 40C şi 1 atm are densitatea: ρ =1000 kgm-3= 102 kgfs2m-4 1.3.2. GREUTATEA SPECIFICĂ Greutatea specifică a unui lichid omogen este raportul dintre greutatea (G) şi volumul
lichidului considerat (V):
gVmg
VG ργ === (1.2)
Greutatea specifică a lichidului variază cu presiunea şi temperatura. Greutatea specifică a apei distilate la 40C şi 1 atm este: 33 kgfm1000Nm9810 −− ==γ 1.3.3. COMPRESIBILITATEA. Compresibilitatea este o componentă a deformabilităţii corpurilor, care constă în
modificarea volumului lor, la o modificare a stării de eforturi normale, adică a presiunii. Dacă E este modulul de elasticitate al lichidului, coeficientul de compresibilitate Kc al
acestuia este:
E1Kc = (1.3)
Modulul de elasticitate E depinde de lichidul luat în considerare. Acest modul, la aproape toate lichidele, este de acelaşi ordin de mărime ca cel al apei.
2

La temperatura de 00C şi la presiunea de la 1at la 200 at, modulul de elasticitate al apei este:
at19231kgfm192307692Nm10*885,1E 229 === −−
Dacă pentru un volum de lichid V presiunea creste Δp, micşorarea volumului ΔV este dată de legea compresibilităţii:
pVKV c ΔΔ −= la limită VdpKdV c−= (1.4) Semnul minus arată că unei creşteri de presiune îi corespunde întotdeauna o micşorare a
volumului. 1.3.4. VÂSCOZITATEA.
Vâscozitatea este proprietatea lichidelor reale de a se opune mişcării relative a particulelor din care sunt compuse.
Pe orice element de suprafaţă, care separă imaginar două porţiuni de lichid real, se dezvoltă în interior tensiuni tangenţiale τ (eforturi unitare tangenţiale, eforturi tangenţiale de vâscozitate).
Fig.1.1.Forţele şi tensiunile tangenţiale de vâscozitate.
Aceste tensiuni apar în interiorul lichidelor reale în mişcare (hidronamică).La lichidele în repaus (hidrostatică), vâscozitatea nu intervine în calcule, lichidele reale comportându-se ca lichide perfecte.
Se consideră un lichid în repaus situat între două plăci, cea inferioară fixă şi cea de la suprafaţa liberă mobilă (fig.1.1). Experienţa arată că dacă se imprimă plăcii mobile superioare o mişcare de translaţie orizontală cu o forţă Fo, particulele care află în contact cu placa se mişcă cu viteza vh, iar cele în contact cu placa fixă au viteza nulă (mişcarea Couette).
Se constată următoarele: -Lichidul se opune deplasării cu o forţă care depinde de natura lichidului, viteza
plăcii,mărimea suprafeţei de contact dintre placa mobilă şi lichid. -După un timp întreaga masă de lichid dintre cele două plăci se află în mişcare. -Antrenarea straturilor din aproape în aproape, duce la micşorarea vitezei particulelor de
la cea maximă vh în contact cu placa mobilă, la viteza nul a celor aderente cu placa fixă. Aceată mişcare a lichidului se numeşte curgere laminară. Conform ipotezei lui Newton, forţa de legătură tangenţială de vâscozitate ΔFt , care se
dezvoltă pe suprafaţa de alunecare ΔA, dintre două straturi de lichid adiacente, între care există viteza relativă Δv, pe distanţa Δz normală la mişcare,este:
=tFΔ Azv Δ
ΔΔη (1.5)
unde: η = coeficientul dinamic de viscozitate (vâscozitatea absolută,vâscozitatea dinamică) 3

=zv
ΔΔ viteza de alunecare sau gradientul vitezei pe normală.
Efortul tangenţial de viscozitate mediu τm este:
AFt
m ΔΔ
τ = (1.6)
Efortul tangenţial de vâscozitate într-un punct este
AF
lim t
ΔΔ
τ = =zvlim
ΔΔη± =
dzdvη± (1.7)
0A →Δ 0z →Δ Din relaţia (1.7) rezulră că gradientul vitezei este derivata vitezei v în raport cu
normala z dusă pe direcţia miscării. Semnul ± apare în relaţie, deorece τ este întotdeauna pozitiv (deci se ia semnul pozitiv când derivata este pozitivă, şi semnul negativ când derivata este negativă).
Din relaţia (1.7) rezultă coeficientul de viscozitate dinamică:
dzdvτη = Nsm-2 ; kgfsm-2 (1.8)
În aplicaţiile practice se foloseşte coeficientul cinematic de vâscozitate:
ρην = m2s-1 (1.9)
Inversul vâscozităţii dinamice este fluiditatea:
η
ϕ 1= m2(Ns)-1 ; m2(kgfs)-1 (1.10)
Vâscozitatea variază puţin cu presiunea, dar apreciabil cu temperatura. 1.4. FORŢELE CARE ACŢIONEAZĂ ASUPRA FLUIDELOR. 1.4.1. FORŢE MASICE EXTERIOARE. Forţele masice exterioare (forţe de volum) se datorează câmpurilor de forţă exterioare
(ex: câmpul gravitaţional), care acţionează asupra volumului de lichid considerat. In hidraulică se iau în considerare forţele de greutate datorate câmpului gravitaţional
terestru, şi forţele de inerţie datorate mişcarii, care sunt tot forţe masice esterioare. Forţele masice exterioare sunt de ordinul de mărime a elementului de masă dm=ρdV a
particulei de fluid considerat. Rezultanta forţelor masice R
rcare acţionează asupra particulei este:
dVfdmfR ρrrr
== (1.11) unde f
r este forţa masică unitară (forţa ce revine unităţii de masă) ale cărei
dimensiuni sunt identice cu cele ale acceleraţiei ( a.1f rr= ).
4
Componentele vectorilor Rr
şi fr
în sistemul ortogonal de referinţă Oxyz sunt:
kRjRiRR zyx
rrrr++= ; kfjfiff zyx
rrrr++= (1.12)
Rx=fxdm=ρfxdV ; Ry=fydm=ρfydV ; Rz=fzdm=ρfzdV (1.13)
2z
2y
2x RRRR ++= ; 2
z2
y2
x ffff ++= (1.14)

1.4.2. FORŢE MASICE INTERIOARE. Forţele masice interioare se datorează atracţiei newtoniene dintre particulele din
interiorul volumului de lichid considerat. Conform principiului egalităţii dintre acţiune şi reacţiune, forţele masice interioare se
anulează două câte două, rezultanta lor fiind nulă. 1.4.3. FORŢE DE CONTACT EXTERIOARE. Forţele de contact exterioare (forţele de legătură exterioare, forţele de suprafaţă
exterioare) care se exercită în lungul suprafeţelor de separare dintre fluidul considerat şi alte medii.
Considerăm o suprtafaţă A a fluidului în contact cu un mediu exterior, în punctul M corespunzând elementul de arie dA (fig.1.2)
5
dATFd
Forţele de contact infinitezimale, sunt forţe de ordinul de mărime ale suprafeţei de contact
rr (1.15) =
Fdr
este forţa elementară de contat Fig.1.2.Efortul unitar de suprafaţă T
r este efortul unitar de suprafaţă sau vectorul
tensiune, sau simplu tensiune. Dacă notăm cu versorul normalei la elementul de arie dA, vectorul tensiune nr T
r
depinde de vectorul de poziţie rr , versorul nr şi timpul t :
T )t,n,r(T rrrr= (1.16)
1.4.4.FORŢE DE CONTACT INTERIOARE.
Forţele de contact interioare (de legătură interioare, de suprafaţă interioare) se
exercită între două suprafeţe contigue ale aceluiaş fluid. Forţele de contact interioare au aceeaş expresie ca forţele de contact exterioare. Pe suprafaţa de arie A, dintre domeniile I şi II, având orientarea definită de versorul
, (fig.1.3.a), forţele de contact interioare sunt supuse principiului acţiunii şi reacţiuniii, adică rr
. nr
Fd Fd−=
Fig.1.3.Forţa de comtact interioară
Forţa elementară de contact Fd
r se descompune într-o componentă normală şi una
tangenţiala pe aria dA (fig.1.3.b):

dATFd nn
rr= ; dATFd tt
rr= (1.17)
unde şi sunt tensiunile normale respectiv tensiunile tangenţiale la elementul de arie dA.
nTr
tTr
1.4.5. PRESIUNEA. FORŢE DE PRESIUNE
În mediile fluide, în general există eforturi unitare de compresiune. În repaus, efortul unitar T trebuie să aibă direcţia versorului n , adică r
0Tt =r
şi npTT nrrr
== (1.18) unde mărimea scalară p ( ) se numeşte presiune ( presiunea hidrostatică). 0≥ Pentru o forţă normală ΔP pe aria ΔA, se defineşte presiunea astfel:
p = limdAdP
AP=
ΔΔ (1.19)
0A →Δ iar dP = pdA (1.20) defineşte mărimea (modulul) forţei elementare de presiune hidrostatică din punctul considerat.
dAnpPd rr= (1.21)
Mărimea forţei de presiune hidrostatică, aferentă ariei A este: P = (1.22) ∫∫ =
AApdAdP
Din relaţia (1.18) rezultă prima proprietate a presiunii hidrostatice: presiunea
hidrostatică este întotdeauna normală la suprafaţa pe care se exercită, şi caracterizeză starea de compresiune.
A doua proprietate a presiunii hidrostatice, constă în faptul că, mărimea presiunii într-un punct nu depinde de orientarea elementului de suprafaţă aferent, ea fiind o mărime scalară.
Fig1.4.Particula de lichid acţionată de forţele masice şi de contact.
Pentru a demonstra proprietetea a doua a presiunii, se consideră o particulă de lichid în formă de tetraedru drept MBCD, de dimensiuni dx, dy, dz. punctul M, fiind originea sistemului de referinţă Mxyz.
Masa elementară a
tetraedrului este
6dxdydzdVdm ρρ == (1.23)
Notăm cu dA aria triungiului BCD şi cu α, β, γ, unghiurile normalei nr la dA, respectiv a ariei dA, faţă de axele de coordonate.
Particula de lichid s află în echilibru sub acţiunea: 6

-Rezultantei forţelor masice de componente:
6dxdydzfR xx = ;
6dxdydzfR yy = ;
6dxdydzfR zz = (1.24)
-Forţele de contact (forţele elementare de presiune hidrostatică):
2dydzpdP xx = ; αcosdApdP AAx = =
2dydzpA
2dzdxpdP yy = ; βcosdApdP AAy = =
2dzdxpA (1.25)
2dxdypdP zz = ; γcosdApdP AAz = =
2dxdypA
Condiţia de exchilibru este:
∑ iX = dPx – dPAx + Rx = 0
∑ iY = dPy -- dPAy + Ry = 0 (1.26)
∑ iZ = dPz – dPAz + Rz = 0
Introducând în relaţiile (1.26), expresiile din (1.24) şi (1.25), efectuând se obşine:
px -- pA + 3dxf xρ = 0
py -- pA + 3dyf yρ = 0 (1.27)
pz -- pA + 3dzf zρ = 0
Trecând la limită, tetraedrul elementar devine punctul M, adică dx=dy=dz=0, aşa
încât relaţiile (1.26) devin: px -- pA = 0 ; pz -- pA = 0 ; pz -- pA = 0 (1.28)
de unde: px = py = pz = pA = p (1.29)
Deoarece orientarea suprafeţei elementare BCD este aleasă arbitrar, mărimea presiunii
este independentă de orientarea feţelor tetraedrului elementar, de unde rezultă caracterul scalar al presiunii hidrostatice.
Dacă elementul de suprafaţă infinit mic dA are coordonatele M(x,y,z), rezultă că presiunea în puntul M depinde numai de coordonatele acestuia şi de densitatea ρ a lichidului:
p = p(ρ,x,y.z) (1.30) In cazul lichidelor omogene ρ = constant, avem: p = p(x,y,z) (1.31)
presiunea fiind numai funcţie de coordonatele punctului considerat. Diferenţiala totală a acestei funcţii uniforme este:
dp = dzzpdy
ypdx
xp
∂∂
+∂∂
+∂∂ (1.32)
Rezultă că pentru cuadrica presiunilor din jurul unui punct M(x,y,z), din masa unui lichid în repaus (echilibru), forma cuadricei este o sferă.
7

8
1.4.6. UNITĂŢILE DE MĂSURĂ ALE PRESIUNII. Unităţile de măsură ale presiunii au dimensiunile unui efort unitar: -În sistemul internaţional (SI). . . . . . . . . . . . . . . .Nm-2; 1Nm-2= 1Pascal -În sistemul tehnic (MKfS). . . . . . . . . . . . . . . . . . kgfm-2 In sistemul tehnic este răspândită atmosfera tehnică:
1 at = 104 kgfm-2 = 1 kgfcm-2
Deasemeni se folosesc şi unităţile piezometrice cum sunt mH2O şi mmHg . Relaţiile dintre diverse unităţi de presiune sunt:
1 kgfm-2 = 9,81 Nm-2 ; 1 at = 98100 Nm-2 = 9,81 kNm-2 = 10 tfm-2 = 0.958atm (atmosfera fizică) = 10 mH2O (+4oC) = 735,5 mmHg(0oC) = 103 bar.
Atmosfera fizică: 1 atm = 10333 kgfm-2.

2. S T A T I C A L I C H I D E L O R
Statica lichidelor (Hidrostatica) studiază repausul (echilibrul) lichidelor şi al solidelor
cufundate parţial sau total în lichid. Lichidele fiind în repaus, particulele componente nu au viteze relative între ele, aşa
încât se face abstracţie de vâscozitate. Forţele care acţionează asupra lichidelor, în hidrostatică sunt: -Forţele masice exterioare, în cazul repausul lichidelor, cea mai obişnuită fiind
greutatea, datorată câmpului gravitaţional terestru. În cazul repausului (echilibrului) relativ, când lichidul este în repaus faţă de un sistem de referinţă mobil, sistem care execută o mişcare faşă de unsistem de referinţă fix, pe lângă forţa de greutate apar şi forţele de inerţie specifice mişcării.
-Forţele de contact (de suprafaţă), care au rolul forţelor de legătura din statica solidelor, care în cazul lichidelor sunt forţe de presiune, respectiv compresiuni pe suprafaţa considerată.
2.1. ECHILIBRUL HIDROSTATIC. 2.1.1. ECUAŢIILE LUI EULER Izolăm dintr-un lichid, o particulă elementară paralelipipedică având muchiile dx, dy,
dz, paralele cu axele sistemului de referinţă, care are masa elementară dm = ρdV = ρdxdydz. Asupra particulei de lichid în repaus acionează forţele (fig.2.1):
Fig,2.1.Echilibrul hidrostatic
-Forţele masice:
Rx = fxρdxdydz ; Ry = fyρdxdydz ; Rz = fzρdxdydz (2.1) -Forţele de legătură (contact) respectiv forţele elementare de presiune hidrostatică:
dPix = pdydz ; dP2x = dydzxpp ⎟⎠⎞
⎜⎝⎛
∂∂
+
9

dP1y = pdzdy ; dP2y = dzdxdypp ⎟⎟⎠
⎞⎜⎜⎝
⎛ ∂+ (2.2)
dP1z = pdxdy ; dP2z = dxdyzpp ⎟⎠⎞
⎜⎝⎛
∂∂
+
Condiţiile de echilibru sunt: ∑ iX = dP1x – dP2x + Rx = 0
∑ iY = dP1y – dP2y + Ry = 0 (2.3)
∑ = dP1z – dP2z + Rz = 0 iZIntroducând în relaţiile (2.3) relaţiile (2.1) şi (2.2), şi efectuând operaţiunile obţinem:
xp∂∂ = ρfx
yp∂∂ = ρfz (2.4)
zp∂∂ = ρfz
relaţii care reprezintă ecuaţiile lui Euler, denumite şi ecuaţiile diferenţiale ale echilibrului hidrostatic.
Relaţiile (2.4) sunt expresia analitică a echilibrului hidrostatic.Expresia vectorială, rezultă din înmulţirea relaţiilor (2.4) cu versorii fundamentali ,k,j,i
rrr şi adunarea acestora astfel
încât:
( )kfjfifkzpj
ypi
xp
zyx
rrrrrr++=
∂∂
+∂∂
+∂∂ ρ (2.5)
respectiv grad p = ρ fr
(2.6)
sau fpr
ρ=∇ (2.7) reprezintă ecuaţia vectorială de echilibru hidrostatic.
În relaţiile (2.6) şi (2.7) este pus în evidenţă operatorul diferenţial, cu caracter vectorial “gradient”
grad = ∇=∂∂
+∂∂
+∂∂
zk
yj
xi
rrr
unde “ ” se numeşte “operatorul nabla” sau “operatorul lui Hamilton”. ∇Din relaţiile (2.6) şi (2.7) rezultă că în cazul lichidelor în repaus vectorul f
rρ este normal
la suprafeţele echipotenţiale (izobare). La stabilirea forţelor de presiune (legătură) s-a admis că: -Pe fiecare faţetă a paralelipipedului elementar, conturate în jurul punctului C(x,y,z).
presiunea p, este aceiaşi, conform propeietăţii a doua apreiunii. -La o deplasare din punctul C(x.y.z) înpunctul E(x+dx,y+dy,z+dz) pe diagonala , de proiecţii dx.dy,dz, presiune p creşte uniform şi liniar, în funcţie de creşterea
coordonatelor x,y,z, cu diferenţele aferente
sdEC rr=
.dzzp;dy
yp;dx
xp
∂∂
∂∂
∂∂
Rezultă deci că presiunea p admite o singură valoare într-un punct de coordonate x,y,z, iars creşterea presiunii dp este dată de diferenţiala totală:
dp = dzzpdy
ypdx
xp
∂∂
+∂∂
+∂∂ (2.8)
10

2.1.2. ECUAŢIA GENERALĂ DIFERENTIALĂ A HIDROSTATICII. Dacă înmulţim ecuaţiile lui Euler (2.4) cu dx, dy. dz, şi le însumăm, obţinem
următoarea relaţie analitică:
( )dzfdyfdxfdzzpdy
ypdx
xp
zyx ++=∂∂
+∂∂
+∂∂ ρ (2.9)
Dar relaţia din stânga egalităţii este dp, respectiv diferenţiala totală a presiunii p (x,y,z) iar relaţia din parantezele din dreapta egalităţii, reprezintă expresia analitică a lucrului mecanic elementar dL al forţei unitare masice f
r al cărei punct de aplicaţie se deplasează pe distanţa
,sdEC rr= produsul vectorial scalar dintre cectorii f
rşi sdr ( sd.fdL rr
= ). Relaţia (2.9) devine:
dp = ρ(fxdx + fydy + fzdz) = ρdL (2.10)
care este expresia analitică a ecuaţiei generale diferenţiale a hidrostaticii şi exprimă legea fundamentală de variaţie a presiunii hidrostatice p, când punctul de aplicaţie al forţei unitare masice f, se deplasează în interiorul lichidului omogen, de densitate ρ, aflat în repaus, pe distanţa ds.
dLdp=
ρ (2.11)
unde dp/ρ este lucrul mecanic elemetar al forţelor elastice, adică al forţelor de presiune. Expresia vectorială a ecuaţiei generale diferenţiale a hidrostaticii, rezultă din
înmulţirea scalară a relaţiei (2.6) cu vectorul sdr , aşa încât pentru câmpul ( z,y,xf )r
se obţine: dp = grad p. sdr = sd.f rr
ρ = ρdL (2.12) căreia îi corespunde ecuaţia anlitică (2.9) repectiv (2.10).
2.1.3. POTENŢIAL. SUPRAFEŢE ECHIPOTENŢIALE.
2.1.3.1. FUNCŢIE DE FORŢĂ. POTENŢIAL.
Dacă componentele forţei unitare masice fx, fy, fz, sunt derivatele parţiale de ordinul întâi în raport cu coordonatele respective ale funcţiei scalare U(x,y,z), care reprezintă un câmp scalar, numită funcţie de forţă, avem:
xUf x ∂∂
= ; yUf y ∂∂
= ; zUf z ∂∂
= (2.13)
deci
gradUkzUj
yUi
xUf =
∂∂
+∂∂
+∂∂
=rrrr
(2.14)
forţa fr
se numeşte forţă conservativă. Se cunoaşte că, lucrul mecanic al foţelor conservative, depinde numai de poziţia iniţială
şi finală a punctului de aplicaţie al acestor forţe, fiind independent de drumul parcurs între cele două poziţii.Astfel:
dUdzzUdy
yUdx
xUsd.gradUsd.fdL =
∂∂
+∂∂
+∂∂
===rrr
(2.15)
şi ţinând seama de relaţia (2.10) rezultă: dp = ρdL = ρdU (2.16)
Dacă în locul funcţiei de forţă U(x,y,z), introducem funcţia potenţială V(x,y,z), între care există relaţia:
U(x,y,z) = - V(x,y,z) (2.17)
11

avem: - =xfxV∂∂ ; fy = -
yV∂∂ ; fz = -
zV∂∂ (2.18)
adică gradVf −=r
= gradU (2.19) astfel încât spunem că forţa unitară masică f derivă dintr-un potenţial şi rezultă că: dp = ρdL = ρdU = -ρdV (2.20)
Funcţia potenţială V(x,y,z) se numeşte energia potenţială a câmpului de forţe, sau pe scurt potenţialul.
Semnul minus din faţa gradientului potenţialului, arată că indensitatea câmpului creşte când potenţialul scade şi invers, ceea ce înseamnă că forţa de câmp este dirijată în sensul în care potrnţialul descreşte.
2.1.3.2. SUPRAFEŢE ECHIPOTENŢIALE. PROPRIETAŢI. Considerăm două puncte din interiorul unui lichid în repaus, situate la adâncimi
diferite,cărora le corepunde o diferenţă de potenţial V = V0, pentru care există o diferenţă de presiune p = p0. In acest caz avem:
(2.21) ∫ ∫−=p
p
V
V0 0
dVdp ρ
p – p0 = -ρ(V –V0) (2.22) sau p + ρV = p0 + ρV0 (2.23) Rezultă că fiecărui punct din lichid îi corespunde o presiune bine definită p. Dacă se unesc toate punctele de aceiaşi presiune,se obţine o suprafaţă echipotenţială
(suprafaţă de nivel, suprafaţă izobară). Aşa dar suprafaţa echipotenţială este locul geometric al punctelor de egal potenţial
(egală energie potenţială), adică: p = p0 – ρ(V –V0) = constant (2.24)
deci dp = 0 (2.25) Cum însă 0≠ρ este evident că:
dL = 0 ; dU = 0 ; dV = 0 (2.26) şi fxdx + fydy + fzdz = 0 (2.27) respectiv produsele vectoriale scalare:
0sd.gradVsd.gradUsd.f =−==rrrr
(2.28) Rezultă că vectorii din relaţia (2.28) sunt perpendiculari între ei, ceea ce înseamnă că
forţa masică unitară este normală pe suprafaţa echipotenţială. Relaţiile (2.24)….(2.28) reprezintă ecuaţia suprafeţelor echipotenţiale, deoarece
satisface condiţia : V = constant. O suprafaţă liberă a unui lichid, în care presiunea atmosferică este constantă, este o
suprafaţă echipotenţială. Proprietăţile suprafeţelor echipotenţiale: -In fiecare punct al unei suprafeţe echipotenţiale forţa masică unitară f este normală
pe suprarfaţă, conform relaţiei (2.28). -Forţa unitară masică f este dirijată în sensul cresterii presiunii şi descreşterii
potenţialului din care derivă. -Suprafeţele echipotenţiale nu se pot intersecta. In caz contrar în intersecţie lor ar
trebuie să existe simultan presiuni diferite ceea xe nu este posibil fizic. -Suprafeţele echipotenţiale sunt izodense. Intrucât presiunea p şi potenţialul sunt
contante, este evident că şi densitatea ρ este constantă. -Suprafeţa de separaţie a două lichide nemiscibile aflate în repaus, este o suprafaţă
echipotenţială. 12

-Suprafeţele echipotenţiale în câmpul gravitaţional radial sunt sfere concentrice. -Suprafaţa liberă a unui lichid în repaus,în anumite limite spaţiale, se consideră o
suprafaţă echipotenţială plană şi orizontală. 2.2. LEGEA HIDROSTATICII ÎN CÂMPUL GRAVITAŢIONAL
TERESTRU. 2.2.1. ECUAŢIA FUNDAMENTALĂ A HIDROSTATICII. Intr-un volum de lichid în repaus, aflat sub acţiunea câmpului gravitaţional terestru
forţele masice derivă numai din acest câmp, fiind egală cu acceleraţia gravitaţională (fig.2.2.a)
Fig.2.2. Presiunea în câmpul gravitaţional terestru
kgf
rr−= ; f = fz = -g ; fx = fy = 0 (2.29)
aşa încât relaţia (2.10) devine: dp = fzdz = -ρgdz = -γdz (2.30) Considerăm un volum de lichid cu o suprafaţă echipotenţială liberă orizontală, având
punctul M0(x0,y0,zo), în care presiunea este p0 şi alt punct în interiorul lichidului M(x,y,z) în care presiunea este p (fig.2.2.b).
Integrând relaţia (2.30) între punctele M0 şi M avem:
(2.31) ∫ ∫−=p
p
z
z0 0
dzdp γ
obţinem p – p0 = -γ(z - z0) (2.32)
sau ttanconsHp
zpz p0
0 ==+=+γγ
(2.33)
Dar z0 - z = h, deci: p = p0 + γh (2.34)
relaţie denumită ecuaţia fundamentaslă a hidrostaticii: Presiunea hidrostatică într-un punct din masa unui lichid în repaus, este egală cu
presiunea exercitată la suprafaţa liberă (p0), plus greutattea coloanei de lichid (γh) de deasupra punctului considerat, având secţiunea egală cu unitatea, iar înălţimea egală cu ordonata punctului respectiv măsurată până la suprafaţa lichidului, adică ADÂNCIMEA punctului în lichid,
Dacă se neglijează presiunea exercitată pe suprafaţa liberă p = 0, ecuaţia fundamentală a hidrostaticii este:
p = γh (2.35) 2.2.2. INTERPRETAREA ECUATIILOR. Din ecuaţia fundamentală a hidrostaticii, rezultă că presiunea creşte liniar cu
adâncimea (fig.2.3). Dreapta AB se numeşte linia piezometrică, care delimitează diagrama presiunilor.
13

Fig.2.3.Variaţia presiunii cu adâncimea
Încazul lichidelor cu densităţi diferite (fig.2.4), linia piezometrică este frântă, iar
preiunea p într-un punct al adâncimea h este:
Fig.2.4.Variaţia presiunii la lichide cu densităţi diferite
p = γ1h1 + γ2h2 + γ3h3 = γmh (2.36) unde γm este greutatea specifică medie.
Relaţia (2.33) interpretată geometric, este oc sumă de înălţimi, denumite şi sarcini, Astfel:
z este înălţimea (sarcina) de poziţie sau geodezică; p/γ este înălţimea (sarcina) piezometrică;
corespunzătoare presiunii absolute p. Rezultă că pentru orice punct din lichidul în repaus în repaus, suma ănălţimilor de
poziţie şi piezometrică Hp este constantă. Relaţia /2.33) interpretată energetic, este o sumă de energii specifice, adică energii
raportate la unitatea de greutate a unei particule:
14

z este energia specifică potenţială de poziţie, faţă de planul de comparaţie orizontal Oxy;
p/γ este energia specifică de presiune. Rezultă că pentru orice punct din lichidul în repaus, suma energiilor specifice de
poziţie şi de presiune este constantă. Dacă înmulţim relaţia (2.33) cu greutatea G = mg = γV a volumului V a lichidului
considerat, avem: mgz + Vp = mgz0 + Vp0 =mgHp = Ep (2.37)
unde: mgz este energia de poziţie a lichidului Vp este energia de presiune a lichidului MgHp = Ep este enrgia totală poteţialî a lichidului în repaus.
2.3. FORŢE DE PRESIUNE PE SUPRAFEŢE PLANE. 2.3.1. FORŢE DE PRESIUNE. CENTRE DE PRESIUNE. 2.3.1.1. MĂRIMEA FORŢEI DE PRESIUNE HIDROSTATICĂ. Se consideră o suprafaţă plană OBDE, înclinată cu unghiul arbitrar α faţă de planul
vertical (fig2.5.a), nivelul apei corespunzând planului Oxy.
Fig.2.5.Forţa de presiune şi centrul de presiune.
Pe planul OBDE se dlimitează o suprafaţă de formă oarecare de arie A, având centrul de greutate în punctul G0.
Considerăm o suprafaţă elemntară dA paralelă cu axa Oy, la distanţa z de axa Oy şi la adâncimea h faţă de nivelul apei.
Forţa elementară de presiune hidrostatică dP ce se exercită pe elementul de suprafaţă dA este:
dP = pdA = γhdA = γzdAcosα (2.38) Forţa de presiune hidrostatică P ce acţionează asupra suprafeţei A, este:
∫ ∫ ∫ ====A A A
hdApdAdPP γγ h0A = γSOxy = γz0Acosα = γSOycosα (2.39)
deoarece conform teoremei momentelor statice, integrala este momentul static
al suprafeţei A în raport cu planul Oxy, adică SOxy= h0A, unde h0 = z0cosα este adâncimea centrului de greutate G0 a suprafeţei A. iar z0A = SOy este momentul static al supeafeţei A în raport cu axa Oy.
∫AhdA
15

Rezultă că mărimea(modulul) forţei de presiune hidrostatică pe care o exercită lichidul pe suprafaţa plană înclinată A, este egală cu greutatea coloanei de lichid de deasupra acestei suprafeţe,de înălţime egală cu adâncimea h0 a centrului de greutate G0 a suprafeţei A
Direcţia forţei de presiune hidrostatică P este normală la suprafaţă, iar sensul este în spre suprafaţa considerată.
2.3.1.2. CENTRUL DE PRESIUNE.
Punctul de aplicaţie al forţei de presiune hidrostatică P se numeşte centrul de presiune C, situat la adâncimea hc , respectiv la zc (fig.2.5)
Poziţia centrului de presiune se determină aplicvând teorema momentelor în raport cu axa Oy (fig.2.5.b):
P.zc = (2.40) ∫A dP.y
sau γh0Azc = γ (2.41) ∫A yhdA
Dar h0 = z0cosα ; h = zcosα (2.42) aşa încât zc.Az0 = (2.43) ∫A
2dAz
unde: z0A = Sy este momentul static al suprafelei A în raport cu axa Oy.
∫A2dAz = Iy este momentul de inertie geonetric a suprafeţei A în rapot cu axa Oy
Relaţia (2.45) devine: zc.Sy = Iy (2.44)
de unde zc = y
y
SI
(2.45)
Conform teoremei lui Steiner: Iy = I0 + (2.46) Az 2
0
unde este momentul de inerţie geometric al suprafeţei în raport cu axa y0—y0 ce trece prin centrul de greutate G0 al suprafeţei A, paralelă cu axa Oy.
0yI
Inlocuind relaţia (2.46) în relaţia (2.45) obţinem:
zc = zo + Az
I
0
y0 = z0 + y
y
SI
0 (2.47)
Insă 2y
y0
0 iA
I= unde raza de inerţie (raza de giraţie), aşa încât obţinem:
zc = zo + 0
2y
zi
0 (2.48)
Diferenţa 0
2y
y
y0c z
iSI
zzz 00 +=+=−=Δ (2.49)
este întotdeauna pozitivă. Rezultă că centrul de presiune C este întotdeauna sub centrul de greutate G0. Această diferenţă scade pe măsura creşterii adâncimii. La adâncimi mari şi pe suprafeţe orizontale diferenţa este nulă.
2.3.1.3. COMPONENTELE FORŢEI DE PRESIUNE. Forţa de presiune hidrostatică P se poate descompune într-o compnentă orizontală Po
şi o componentă verticală Pv: Po = Pcosα = γh0Acosα = γh0Av (2.50) Pv = Psinα = γh0Asinα = γhoAo (2.51) Pv = P0tgα = γh0Avtgα (2.52)
16

Iar: 20
2v0
2v
20 AAhPPP +=+= γ =
αα
cosP
tg1P 020 =+ =
αγcos
Ah vo (2.53)
unde Av este proiecţia lui A pe planul vertical, iar Ao este proiecţia lui A pe planul orizontal. Rezultă că mărimea componentelor P0 şi Pv este egală cu greutatea prismelor de
lichid de volum h0Av, respectiv h0A0.. Considerăm Ai (i = 1…n) suprafaţe plane delimitate de două suprafeţe echipotenţiale
la adâncimi h1 şi h2, situate în plane oblice faţă de planul vertical Oyh cu unghiul aferent αi (fig.2.6).
2.6.Componentele forţei de presiune. Deasemeni considerăm că proiecţia tuturor suprafeţelor Ai pe planul vertical Oyh este
constantă şi egală cu Av = Aicosαi, având adâncimiea centrului de greutate h0 şi adânsimea centrului de presiune hc. Rezultă că:
-Adâncimile centrelor de greutate şi a centrelor de presiune ariilor Ai, se află pe aceeaşi suprafaţa echipotenţială h0, respectiv pe suprafaţa echipotenţială hc.
Dar z0i = i
o
coshα
; zci = i
c
coshα
(2.54)
aşa încât pentru α = 0 avem z0 = h0, iar zc = hc. -Componenta orizontală a forţei de presiune hidrostatică P0 pentru toate suprafeţele
este constantă: P0i = Picosαι = γh0Aicosαι = γh0Av = P0 = constant (2.55) -Componenta verticală a forţei de presiune hidrostatică Pvi variază în funcţie de
unghiul αi: Pvi = Potgαi (2.56) -Forţa de presiune hidrostatică Pi aferentă ariei Ai este:
Pi = P0 i2tg1 α+ =
i
0
cosPα
(2.57)
17

2.3.2. FORŢA DE PRESIUNE PE SUPRAFEŢE DREPTUNGHIULARE. 2.3.2.1. FORŢE DE PRESIUNE PE SUPRAFEŢE PLANE VERTICALE. Barajele rectilinii pentru corectarea torenţilor, au în mod obişnuit paramenţii formaţi
din suprafeţe plane verticale, înclinate, sau combinate. pe care se exercită forţele de presiune hidrostatică.
Considerăm dintr-un parament vertical, un dreptunghi cu baza b = 1 m şi înălţimea Y (m) (fig.2.7) pe care se exercită forţa de presiune a apei limpezi γ = 10 kNm-3, în două variante ale suprafeţei libere.
Aplicând relaţiile (2.39) şi (2.47) obţinem:
P1 = 2Y21 γ = Vph1 = Aoh1 = ; P2 = ( H2YY
21
+γ ) = Vph2 = Aph2 (2.58)
Unde: Vph = volumul prismei presiunilor hidrostatice Aph = suprafaţa diagramei presiunilor în plan vertical.
iar h1 = Y32 ; h2 =
( )( ) =
++
21
21
pp3p2pY ( )
( )H2Y3H6H3YY2 2
+++ (2.59)
şi s1 = Y31 ; s2 = ( )
( )21
21
pp3pp2Y
++ = ( )
( )H2Y3H3YY
++ (2.60)
Fig. 2.7.Prisma presiunilor şi forţa de presiune
Din relaţiile (2.58)….(2.59) rezultă că: -Mărimea forţei de presiune hidrostatică P este de fapt mărimea rezultantei forţelor
elementare de presiune, respectiv volumul prismei presiunilor hidrostatice Vph aferente suprafeţei dreptunghiului A = b.Y = 1.Y, direcţia forţei P normală pe A, trece prin centrul de greutate Gp al prismei presiunilor şi al centrului de presiune C de pe suprafaţa A.
-Pentru determinarea mărimii forţei de presiune şi a poziţiei centrului de presiune, pentru un dreptunghi cu baza b = 1 şi înălţimea Y, este suficientă cunoaşterea mărimii suprafeţelor diagramelor presiunilor Aph, în plan vertical, respectiv suprafaţa unui triunghi sau a unui trapez, şi poziţia centrului de greutate al triunghiului sau al trapezului respectiv
-Orice diagrama trapezoidală se poate descompune într-o diagramă dreptunnghiulară şi una triunghiulară (fig.2.8), aşa încât:
18

Fig.2.8.Descompunerea diagramei presiunilor.
P = P1 + P2 = γYH + 21 γΥ2 = ( H2YY
21
+γ ) (2.61
s1 = Y21 ; s2 = Y
31
; s = 21
2211
PPsPsP
++ = ( )
( )H2Y3H3YY
++ (2.62)
2.3.2.2. FORŢE DE PRESIUNE PE SUPRAFEŢE PLANE OBLICE. Înclinarea paramenţilor barajelor faţă de planul verical este definită de tgα = λ denumit
fructul paramentului (fig.2.9). Pentru un baraj cu profil trapezoidal având fructul paramentului amonte λ = tgα care
poate fi pozitiv (fig.2.9 a şi b) sau negativ (fig.2.9 c şi d), forţa de presiune hidrostatică si componentele acesteia sunt:
19

Fig.2.9. Baraj cu parament amonte înclinat
( )
αγ
cos2H2YYP +
= (2.63)
având componentele
P0 = εcos
P = ( H2YY21
+γ ) ; Pv = αsin
P = ( )λγ H2YY21
+ (2.64)
Centrul de presiune se află la; s = ( )( )H2Y3
H3YY++ (2.65)
2.3.2.3. FORŢE DE PRESIUNE PE SUPRAFETE COMBINATE -Baraj cu fundaţie evazată (fig.2.10.a,b).
Fig.2.10.a.b.Baraj cu fundaţie evazată
) ; s1 = Y - ( )( )H2Y3
H3Y2Y
1
11
++ P1 = ( H2YY
21
11 +γ
P20= ( )H2YY2Y21
212 ++γ ; s2 = Y1+( )( )H2YY23
H3YY3Y
21
212
++++
P2v= ( H2YY2Y21
212 ++γ ) λ; P2 = 2v2
2o2 PP + (2.66)
) ; s3 = ( )( )H2YY23
H2Y2Y2YY
3
213
+−+++
P3 = ( H2YY2Y21
33 +−γ
sau: P0 = ( )H2YY21
+γ ; s = ( )( )H2Y3
H3YY++ (2.67)
20

Pv = eb21 γ (2Υ1+Υ2+2H) ; P = 2
v2
o PP +
-Baraj cu redane (fig.2.10.c)
Fig.2.10.c.Baraj cu redane
) ; s = ( )( )H2Y3
H3YY++ (2.68) P = ( H2YY
21
+γ
P1 = ⎟⎠⎞
⎜⎝⎛ + H
3Yaγ ; P2= ⎟
⎠⎞
⎜⎝⎛ + H
3Y2aγ
-Baraj în consolă (fig.2.10.d)
Fig.2.10.d.Baraj în console.
) ; s = ( )( )H2Y3
H3YY++ (2.69) P1 = ( H2YY
21
+γ
P2 = γa(Y + H) Relaţiile (2,58)….(2.69) confirmă că pentru suprafeţele plane cuprinse între două
suprafeţe echipotenţiale (H şi Y+H) şi cu proiecţie egală[ pe planul vertical (normal pe suprafeţele echipotenţiale), componenta orizontală a forţei fe presiune hidrostatică (P0) este aceiaş ca mărime, iar centrul de presiune ( C ) se află la aceeaşi adâncime.
2.3.3.. PARADOXUL HIDROSTATIC.
Pe fundul orizontal al recipientelor de adâncime h faţă de suprafaţa liberă a lichidului
şi de aceiaş arie A (fig.2.11), conform legii fundamentale a hidrosticii, mărimea forţei de presciune hidrostatică este aceeaşi indiferent de forma recipientului.
P = γ h A (2.70)
21

Fig.2.11.
Centrul de presiune se suprapune cu centrul de greutate al suprafeţei A. 2.3.4. CURBA INTEGRALĂ A PRESIUNII 2.3.4.1. DEFINIŢIE. S-a arătat că presiunea hidrostatică variază liniar cu adîncimea (fig,2.12.a), linia fiind
denumită linia piezometrică.
Fig.2.12.Linia pizometrică şi curba integrală a presiunii
2z
0
z
0z z21dz.1.zdPP γγ === ∫∫ (2.71)
de unde rezultă că forţa de pesiune hidrostatică variază parabolic cu adâncimea fig.2.12.b) parabola numindu-se curba integrală a presiunii.
Derivând relaţia (2.71) în raport cu z obţinem:
zpdzdP
zz γ== (2.72)
adică presiunea hidrostatică la adâncimea z.
2.3.4.2. APLICAŢIE Cu ajutorul curbei integrale a presiunii, diagrama presiunilor hidrostatice se poate
împărţi în părţi proporţionale sau egale aferente forţelor de presiune hidrostatice
22

Fig.2.13.Forţe de presiune egale cu adâncimea.
Să considerăm suprafaţa unui stăvilar A = Y.1 (m2), care se consolidează cu n
lonjeroni de aceiaş secţiune (fig.2.13). Rezultă că fiecărui lonjeron trebuie să-i revină o forţă de presiune hidrostatică egală cu:
2l Y
n21
nPP γ== (2.73)
Inseamnă că problema se reduce la împărţirea suprafeţei diagramei presiunilor care este un triunghi, în suprafeţe egale, cu stabilirea centrelor de greutate aferente, prin care trec direcţiile forţelor Pl , la adâncimea cărora se amplasează lonjeroanele.
Rezolvarea problemei se poate face analitic şi grafic. 1.-Analitic cu ajutorul relaţiei:
niYzi = (2.74)
zi (i=1…n) fiind ordonatela care împart diagrama presiunilor, respectiv triunghiul în suprafeţe egale. Odată cunoscute aceste ordonate,se determină centrele de grutate aferente zci.
2.-Grafic se procedează astfel (fig.2.12): -La o scară convenabilă se trasează diagrama presiunilor şi curba integrală a presiunii. -Se împarte dreapta EB = P în n părţi egale. -Din aceste puncte se ridică perpendiculare, care intersectează curba integrală. -Din aceste puncte de intersecţie se duc dreptele orizontale, care împarte diagrama
presiunilor în suprafeţe egale. -Segmentele egale de pe dreapta EB se împart în jumătate, de unde se ridică iar
perpendiculare care intersecteză curba integrală. -Din aceste puncte de intersecţie se duc drepte orizontale,care determină poziţia
centrelor de greutate, cât şi centrele de presiune unde se amplasează lonjeroanele. 2.4. FORŢE DE PRESIUNE PE SUPARFEŢE CURBE DESCHISE. 2.4.1. MĂRIMEA ŞI DIRECŢIA FORŢELOR DE PRESIUNE Considerăm o suprafaţă curbă oarecare, udată pe osingură parte, şi sistemul de referinţă
Oxyz (fig.2,14). Pe un element de arie dA de coordonate x.y,z, forţa elementară de presiune hidrostatică
dP la adâncimea z este: dP = pdA = γzdA (2.75)
23

Fig.2.14.Forţe de presiune pe suprafeţe curbe.
Proiecţiile forţei elementare dP pe sistemul de axe sunt: dPx = dPcosα1 = γzdAcosα1 = γzdAx
dPy = dPcosβ1 = γzdAcosβ1 = γzdAy (2.76) dPz = dPcosγ1 = γzdAcosγ1 = γzdAz
unde cosα1, cosβ1, cos γ1 sunt cosinuşii directori ai forţei elementare dP: dP = 2
z2
y2
x dPdPdP ++ (2.77) Ariile elementare dAx, dAy, dAz, sunt proiecţiile elementului de arie dA pe planele Oyz,
Ozx, Oxy, normale la axele Ox, Oy, Oz. Proiecţiile Px, Py, Pz, ale forţei de presiune P sunt: ( )OyxxA 0xA xx SAzzdAdPP
xx
γγγ ==== ∫∫
Py= ( )Oxyy0A yA y SAzzdAdP
yy
γγγ === ∫∫ (2.78)
zA zA zz VzdAdPPzz
γγ === ∫∫
unde: z0 este adâncimea centrului de greutate a suprafeţei A; Ax, Ay, Az, sunt proiecţiile suprafeţei A pe planele triedrului Oxyz; (Sx)Oy = z0Ax este momentul static al suprafeţei Ax în raport cu axa Oy; (Sy)Ox = z0Ay este momentul static al suprafeţei Ay în raport cu axa Ox; Vz este volumul de lichid cuprins între suprafaţa curbă A şi proiecţia acestei
suprafeţe Az pe planul suprafeţei libere a lichidului. Din relaţiile (2.78) rezultă: -Componentele orizontale Px şi Py sunt egale cu forţele de presiune hidrostatică
aferente suprafeţelor verticale Ax şi Ay. -Componenta verticală Pz este egală cu greutatea volumului de lichid V al prismei
verticale. Mărimea forţei P este: P = 2
z2
y2
x PPP ++ (2.79) Direcţia forţei P este dată de cosinuşii directori:
24
; PP
cos y=βPP
cos x=α ; PPcos z=γ (2.80)

25
2.4.2. C00RDONATELE CENT UI DE PRE E.
zultă din aplicarea teoremei moment
(2.81)
x x Oy x şi
ariei Ax Oy
RUL SIUN Coordonatele centrului de presiune C (xc yc, zc) reor în raport cu axele de coordonate. el
-In raport cu axa Oy, pentru forţa Px: zcPx = ∫
xA
Dar P = γ(S ) iar dP
xzdP
= γzdAx yxAIdAz
x
=∫ (momentul de inerţie axial al2
în raport cu axa ), aşa încât:
( ) x0
y
Oyx
yc
IIz =
AzS= (2.82)
În mod analog se obţin coordonatele calculând m-În raport cu axa Oz pentru forţa P :
omentele: x
( ) x0
yzyz IIy ==
Oy Az (2.83)
unde Iyz este momentul de inerţie centrifugal al suprafeţei -In raport cu axa Ox pentru forţa Py:
xc S
Ax. în raport cu axele Oy şi Oz.
( ) y0
xx IIz == (2
OxAz
.84)
unde Ix este momentul de inerţie axial al suprafeţei Ay în-În raport cu axa Oz pentru forţa Py:
yc S
raport cu axa Ox.
( ) y0
xzxz IIx ==
OxAz
(2.85)
unde Ixz este momentul de inerţie centrifugal al suprafeţei Deci coordonatele centrului de prersiune sunt
yc S
Ay în raport cu axele Ox şi Oz.
yc S
xzIx = ;
xc S
yzIy = ;
y
xyc
IIz == (
x SS2.86)
2.4.3. APLICAŢIE.
idrostatică P şi coordonatele centrului de presiune C, pe un tronson de param vertical al unui baraj curb, de un sfert de cilindru şi înălţime h (fig.2.15
Forţa de presiune h
ent amonte ) este:
Fig.2.15,Baraj cu parament amonte curb.
Ax = Ay = rh ; Ay = 0 ; z0 = h1 ; Sx = Sy = z0A 2rh21
2 x = ;

26
Px = Py = γSx = 2rh1 γ ; Pz = 0 ; P = 22y
2x PP =+ rh
22 γ
2
1P
tg y ==α ; 50 ; xc = yc = rcos4 r22
Px
α = 4 50 = ; zc = h32
2.5. PLUTIREA CORPURILOR
V şi greutate G, în echilibru, într-un lichidn în repaus.
hidrostatică dPx, dPy, dPz. (fig.2.16 )
. 2.5.1, LEGEA LUI ARHIMEDE. Considerăm un corp solid de volum
Pe suprafaţele elementare de contact cu lichidul, acţionează forţele elementare de presiune
Fig.2.17. Principiul lui Arhimede Componentele forţelor Ox şi Oy sunt nule, fiindcă
sunt câte două, egale, pe aceeaşi direcţie şi de sens contrar. Rezultă că:
(2.88)
(2.8ă, flo tatea, s
sus.
Un corp cufundat parţial sau total într-un lichid în repaus,este suspus unei forţe ascensio d dislocuit de corp.
.2. CONDIŢIA DE PLUTIRE.
G şi PA pentru un corp cufundat parţial sau total, se disting următoarele cazuri:
de presiune hidrostatică după axele
dPz = dP1z – dP2z =γ(z1 – z2)dAz = - γhdAz (2.87) iar rezultanta este: Pz = ∫ zdP = - ∫ hdAγ = - γV = - PA
A A
8) reprezintă forţa arhimedică (portanţa hidrostatică, forţa de sub Expresia împingere, forţa ascensional tabili au simplu portanţa) care este dirijată de jos în
Legea (principiul) lui Arhimede are următorul enunţ:
nale, egală ca mărime cu greutatea volumului de lichiVolumul lichidului dislocuit se numeşte volum de carenă sai simplu carenă, dacă corpul
pluteşte la suprafaţă. Centrul de greutate al volumului dislocuit se numeşte centru de presiune sau centru
de carenă. 2.5 După raportul dintre mărimile forţelor
G < PA corpul se menţine la suprafaţa lichidului, fiind în starea de plutire la suprafaţă ;

27
PA corpul ajunge la fund unde rămânr în echilbru, Reacţ (2.89)
unde γψ
CILINDRICI.
orului sub linia de plutire. onsiderăm un plutitor cilindric (ex: un buştean) de lungime l, rază r, greutate
specifică
G = PA corpul se află în starea de plutire submarină(cufundată) G >iunea rezemării pe fund este: N = G – PA =(γc - γ )V
este greutatea specifică a corpului. 2.5.3. PESCAJUL PLUTITORILOR Pescajul unui plutiror este adâncimea maximă a plutitC γc şi un pescaj h (fig,2.17).
Fig.2.17.Pescajul plutitorului cilindric
Aplicând condiţia G = PA avem:
⎟⎠⎞
⎜⎝⎛ −=−
22sinr
2cossin2r 22 ϕϕϕϕ (2.90) Allrr 2
c γπγ = ; = rA 2ϕ
⎟⎠⎞
⎜⎝⎛ −=
22sinlrlr 22
cϕϕγπγ (2.92)
de unde: 2π ( )hf2sin2c =−= ϕϕγγ
(2.93)
iar h = r(1 – cosφ) (2.94) Calculul direct al pescajului cu relaţia (2.93) nu este posibilă, aşa încât aceasta este
articule solide, formându-se
n amestec intim, rezultând astfel un fluid bifazic = apă+aluviuni.
elei exercitate numai de apa limpede.
e consideră fluidul bifazic = apă+aluviuni ca un amestec omogen, având greutatea specifică
ifică a apei limpezi;
unilor în curentul de apă (raportul dintre debitul volumi rentului de apă care le transportă - m3s-1-), care practic are valorile η = 9,2…o,4.
transpusă în nomograme. Dacă se determină indirect unghiul φ pescajul se determină cu relaţia (2.94). 2.6. FORŢA DE PRESIUNE A APEI CU ALUVIUNI. 2.6.1. PRESIUNEA HIDROSTATICĂ A APEI CU ALUVIUNI.
Viiturile torenţiale, datorită eroziunii solului, antrenează pu
În acest context presiunea acestui fluid, respectiv forţa de presiune acestui mediu fizic, exercitată asu pra lucrărilor hidrotehnice este evident superioară c
Sunt două posibilităţi de determinarea presiunilor: S echivalentă γe:
γe = γ + η(γp - γ) (2.95)
unde: γ = greutatea specγp = greutatea specifică a aluviunilor (pământului) nesubmersat; η = coeficientul de încărcare al aluvic al materialelor transportate de curent – m3s-1- şi debitul cu

28
t la adâncimea z este :
nea datorită împing
Greutatea specifică echivalentă a fluidului bifazic poate ajunge la 1,5….1,8 ori greutatea specifică a apei limpezi, în cazul torenţilor noroioşi şi a apei de piatră.
Presiunea hicrostatică a fluidului bifazic într-un punc pz = γez (2.96)
b)Se consideră separat presiunea hidrostatică a apei p1z = γz şi presiuerii active a aluviunilor submersate p2z = γszpK (fig.2.18).
Fig.2.18.forţa de presiune a apei încărcată cu aluviuni
Prin suprapunerea efectelor: pz = p1z + p2z = γυ + γszpK 2.97)
unde: γs = greutatea specifică a aluviunilor(pământului) submersate, care este egală cu: γ
ământului şi 2.99)
când slu:
. . . . . . . . . . . ..n = 25%….50% . . . . n = 70%….90%
compoziţia chimică ca material predom
(
σ = γp - γ (2.98) când nu se ia în considerare pororzitatea p
γσ = (1 – n)(γp - γ) (e ia în considerare porozitatea pământului. Porozitatea variază în limite foarte largi, de exemp-nisipuri şi nisipuri neuniforme . . . . . . . . . . . . . . . . . . . . . . n = 15%….30% -nisipuri uniforme . . . . . . . . . . . . . . . . . . . . . -argile sedimentate recent, măluri . . . . . . . . . . . . . . . .γp = greutatea specifică a pământului nesubmersat, care dacă se ţine seama de a acestuia, valoarea uzualaă este γp = 26,5 kNm-3 adică cea a cuarţuluiinant în nisip. zp= adâncimea aluviunilor aluviunilor submerasate al căror nivel se află la pragul
deversorului (fig2.17),când efectul împingerii active a pământului submersat esste maxim, adică pe toată înălţimea Y.
K = coeficientul de împingere activă a pământului submersat, care pentru paramenţii verticali este:
KP = tg2(450 - 2ϕ ) (Poncelet) (2.100)
KR = ϕϕ
sin1+sin1− (Rankine) (2.101)
unde φ = unghiul mediude frecare a pămânzului în stare de submersie.
ice echivalente γe (apă+aluviuni) ste pentru parament amonte vertical:
2.6.2. FORŢA DE PRESIUNE P A APEI CU ALUVIUNI.
Forţa de presiune hidrostatică în cazul greutăţii specife

P = ( )H2YY1+γ (2.102)
2 e
Pentru parament amonte oblic:
P = ( )
m
e
cos2H2YY
αγ +
(2.103)
iunii apei şi a F = P + E (2.104)
unde
In cazul suprapunerii efectelor acţ aluviunilor submersate,forţa totală este:
29
( )H2YY2
P += γ ; E = 1 KY2 sγ (2.105) 1 2
Pentru parament amonte oblic: ( )
m m
2s
cos2KY
Eα
γ=
c2P
osH2YY
αγ +
= ; (2.106)
orţei F se dete
RELATIV.
care, conform principiului lui d’Alembert: forţele de inerţie echilibrează în orice moment rezultanta forţelor date (acive)
Centrul de presiune al f rmină aplicând teorema momentelor.
2.7. ECHILIBRUL RELATIV.
2.7.1. DEFINITIA ECHILIBRULUI Se cunoaşte că în cazul corpurilor în miş
ri dF amr= R
r şi a
forţelor de legătur pas e) lRr
:
ă ( iv
ld RRamrrr
+= (2.107)
sau 0lR)amR( d =+−rr
(2.108) rrr
unde Φ=− amRd este vectoru sau forţa pierdută. Acest principu nu este un principiu ă reducă problema dinamicii la una de
l lui d’Alembert fizic în stare s
statică re ică de echili căruia matematic problem
ală, ad bru real, ci este un principiu analitic, cu ajutorul a de dinamică se transformă într-una statică, definită ca echilibru relativ (fictiv), de unde
şi denumirea de metoda cineto-statică. Conform principiului lucrului mecanic virtual, lucrul mrcanic virtual al forţei Φ
r
pentru orice deplasare virtuală rrδ compatibilă cu legăturile este nulă, adică: 0r.L =−
rrδΦδ (2.10
In cazul fluidelor, acţion e de forţe masice, pentru o particulă de flui9)
at d de masă unitară m = 1 de condiţia de e pe suprafaţa echipotenţială, chilibru este:
dp = ρdL = =sd.f rrρ ρ (fxdx + fydy + fxdy) = 0 (2.110)
2.7.2. SUPRAÎNĂLŢA CURBA
racordate prin arc de cerc (fig.2.19)
REA APEI ÎN CANALELOR . Considerăm două aliniamente de canal dreptunghiular

Fig.2.19..Supraînălţarea apei în curbă
Pentru o particulă de lichid de masă unitară m = 1, care se află în mişcare în curbă cu
viteza constantă v, pe o suprafaţă liberă, care este o suprafaţă echipotenţială, deci dp = 0, acţionează forţa masică unitară exterioară fz = -g datorită câmpului gravitaîional terestru şi forţa unitară de inerţie centrifugă fx=v2/x, care este tot o forţă masică, aşa încât:
fxdx + fydy + fzdz = 0 (2.111)
de unde: 0gdzx
dxv2 =− (2.112)
Prin integrare se obţine: Cxlngvz
2
+=
Pentru x = ri ; z = 0 iar i
2
rlngvC −= aşa încât:
( )i
2
i
2
rxln
gvrlnxln
gvz =−= (2.113)
Pentru x = re z = i
e2
rr
lngvz =Δ (2.114)
sau: i
e2
rr
lggv303,2z =Δ (2.115)
Relaţiile (2.114) şi (2.153) dau supraînălţarea totală a apei în curbă faţă de malul interior. Practic se ia 2/zΔ faţă de nivelul liber al apei la intrarea în curbă din aliniamentul amonte, la care se adaugă o înălţime suplimentară de siguranţă.
30

3. D I N A M I C A L I C H I D E L O R
Dinamica lichidelor (Hidrodinamica) studiază mişcarea lichidelor, luând în considerare forţele care acţionează asupra lor.
Cinematica lichidelor (Hidrocinematica) studiază mişcarea lichidelor, fără a ţine seama de forţele ce acţionează asupra lor, deci se studiază geometria mişcării, ceea ce este necesar dar nu şi suficient.
In mecanica lichidelor se reprezintă mişcarea sistemului de particule lichide care alcătuiesc volumul de lichid considerat.
In hirodinamica tehnică (aplicată) nu interesează particulele individuale, ci masa de lichid în ansamblul ei, stabilind vitezele, acceleraţiile, presiunile, etc., în fiecare punct al spaţiului în funcţie de timp,în funcţie de sistemul de referinţă adoptat (coordonate carteziene, cilindrice, sferice, etc.), cât şi de sistemul de reprezentare a miscării lichidelor (Lagrange, Euler).
Pentru descrierea mişcării lichidelor sunt necesare o serie de notiuni utilizate în elaborarea modelelor matematice cât şi pentru înţelegerea şi interpretarea sensului fizic al mişcării.
3.1. ELEMENTELE MIŞCĂRII LICHIDELOR. 3.1.1. NOŢIUNI FUNDAMENTALE. -Linia de fluid(lichid) este o înşiruire de particule de fluid, care se găsesc în contact în
ipoteza continuităţii mediului. -Traiectoria (fig.3.1) este locul geometric al poziţiilor succesive a unei singure
particule de lichid în mişcare, în raport cu un sistem de referinţă. Pentru timpul to particula se află în punctul Mo(xo,yo,zo), iar pentru timpul t în punctul M(x,y,z), cărora le corespund vectorii de poziţie:
Fig.3.1. Traiectoria Fig.3.2. Linia de curent
oo rr rr= (xo,yo,zo,to) ; )t,z,y,x(rr rr
= (3.1) Ecuaţiile parametrice ale traiectoriei în sistemul de referinţă cartezian sunt:
x = x(xo,yo,zo,t) ; y = y(xo,yo,zo,t) ; z = z(xo,yo,zo,t) (3.2) Eliminând variabila independentă timp t din relaţiile (3.2) rezultă ecuaţia traiectoriei care se referă la o singură particulă de lichid şi are forma:
f(x,y,z,xo,yo,zo) = 0 (3.3) -Viteza locală este viteza particulei ce se află la momentul t în punctul M(x,y,z),adică:
31

)t,z,y,x(vv rr= (3.4)
-Linia de curent (linia de flux sau linia de curgere) este curba tangentă la vectorii viteză locală a mai multor particule de lichid la un moment dat (fig.3.2).
Deci linia de curent este curba înfăşurătoare a vectorilor viteză )t,z,y,x(vr ale unui ansamblu de particule.
Ecuaţia diferenţială a liniei de curent, rezultă din condiţia de paralelism a tangentei la linia de curent cu vectorul viteză:
=sdr λ vdr (3.5) dzkdyjdxisdrrrr
++= ; kvjvivvd zyx
rrrr++= (3.6)
dx= λ vx ; dy= λ vy ; dz= λ vz (3.7)
de unde: zyx v
dzvdy
vdx
== (3.8)
sau : )t,z,y,x(v
dz)t,z,y,x(v
dy)t,z,y,x(v
dx
zyx
== (3.9)
In momente succesive, aspectul liniilor de curent se schimbă şi pe ele apar mereu alte particule.
Dacă viteza locală nu variază în timp, liniile de curent coincid cu traiectoriile. Familia liniilor de curent are următoarele proprietăţi: -Prin fiecare punct din domeniu trece cel puţin o linie de curent,conform ipotezei
continuităţii mediului şi a mişcării; -Printr- un punct nu trece decât o singură linie de curent, cu excepţia punctelor singulare
de viteză nulă sau infinită. Dacă într-un punct ar trece două linii de curent, ar însemna că viteza locală finită ar avea două direcţii ceea ce fizic nu este posibil.
-Liniile de curent se aştern pe un corp în mişcare în interiorul lichidului. -Tub de curent este suprafaţa tubulară generată de liniile de curent care se sprijină pe
o curbă închisă.
Fig.3.3. Tuburi de curent.
-Tub elementar de curent este tubul de curent a cărui secţiune este o suprafaţă
elementară. -Fir de curent este linia fluidă(lichid) din interiorul unui tub elemetar de curent. Când
linia fluidă(firul) de curent este pus în evidenţă prin marcarea particulelor (colorare) aceasta se numeşte linia trasoare.
-Suprafaţa de curent este formată din totalitatea liniilor de curent care se sprijină pe o curbă dată. Când liniile de curent se sprijină pe o curbă închisă, suprafaţa de curent reprezintă un tub de curent (sau tub elementar de curent).
-Suprafaţa (secţiunea ) vie este suprafaţa ortogonală la liniile de curent (fig.3.3). -Curentul de fluid(lichid) este masa de fluid în mişcare limitată de un tub de curent
fiind formată dintr-o infinitate de fire de curent. -Secţiunea curentului (A) este aria secţiunii vii a unui curent unidimensional. In
practică, în cazul albiilor deschise, se foloseşte denumirea de suprafaţă udată sau secţiune
32

muiată, care este aria ocupată de curentul de lichid într-o secţiune transversală pe direcţia generală de curgere.
-Debitul de fluid(lichid) (Q) este cantitatea de lichid ce trece printr-o secţiune în unitatea de timp.
Considerăm o secţiune oarecare dA printr-un tub elementar de curent, caracterizat prin versorul normalei nr (fig.3.4).
Fig.3.4.Debitul de fluid
Debitul elementar de curent dQ este:
dAv)n,vcos(vdAdAn.vdQ n===rrrr (3.10)
unde vn este componenta vitezei normală la dA. Debitul curentului este:
∫ ∫==A A ndAvdAn.vQ rr (m3/s) (3.11)
care se numeşte debit de volum sau flux de viteză, respectiv volumul de lichid ce trece în unitatea de timp prin suprafaţa A.
Debitul de masă (Qm) este masa de lichid ce trece prin suprafaţa A în unitatea de timp: Qm = ρQ (kg/s) (3.12)
Debitul de greutate (Qg) este greutaea de lichid ce trece prn unitatea de timp prin suprafaţa A:
Qg = γQ (N/s) (3.13) -Viteza medie este viteza caracteristică schemei unidimensionale a curentului şi este
dată de raportul dintre debit şi secţiunea curentului, de unde denumirea de viteza debitantă:
V = AQ (m/s) ; Q = AV (m3/s) (3.14)
-Adâncimea curentului (h) este distanţa măsurată pe verticală de la suprafaţa liberă a curentului la fundul canalului sau albiei în general (fig.3.5).
Fig.3.5. Perimetrul udat în canale şi albii .
-Perimetrul udat (P) este lungimea perimetrului pentru secţiuni transversale (a
suprafeţei udate) a curentului unidimensional care este formată din pereţi rigizi. In calculul perimetrului udat nu se ia în considerare linia suprafeţei libere a curentului,
dacă aceasta prezintă o astfel de suprafaţă (fig.3.5) -Raza hidraulică (R) este raportul dintre secţiunea curentului (A)(suprafaţa udată) şi
perimetrul udat (P):
33

R = PA (m) (3.15)
-Adâncimea hidraulică (hm) este adâncimea medie a unui curent cu suprafaţă liberă, dată de raportul dintre suprafaţa udată (A) şi lăţimea curentului la suprafaţa liberă (B) (fig.3.5):
hm= BA (m) (3.16)
3.1.2.CLASIFICAREA MIŞCĂRILOR LICHIDELOR. 3.1.2.1. CRITERII DE CLASIFICARE. Studiul mişcării lichidelor, necesită clasificarea acestora în funcţie de anumite criterii.
a)După criteriul variaţiei în timp a parametrilor locali avem: -mişcări permanente, -mişcări nepermanente.
b)După criteriul variaţiei în spaţiu a parametrilor locali avem: -mişcări tridimensionale, -mişcări bidimensionale, -mişcări unidimensionale.
c)După criteriul condiţiilor de contact, avem: -mişcări sub presiune, -mişcări cu suprafaţă liberă.
d)După criteriul fizic,avem: -mişcări laminare, -mişcări turbulente.
Aceasta reprezintă o clasificare paralelă, deoarece o mişcare poate fi caracterizată simultan ca fiind permanentă, sub presiune, turbulentă, etc. Rezultă că în studiul mişcării lichidelor, trebuie luate în considerare toate caracteristicile specifice.
3.1.2.2. MIŞCĂRI PERMANENTE ŞI NEPERMANENTE. Mişcările permanente (staţionare) sunt mişcările la care parametrii locali (v, p, etc) nu
variază în timp ca mărime şi direcţie, aceştia rămânând constanţi. Deci viteza locală şi presiunea sunt funcţie numai de coordonatele diferitelor puncte din
domeniu, ele fiind constante în tot timpul mişcării lichidului. )z,y,x(vv rr
= ; p = p(x,y,z) (3.17) Rezultă deci următoarele proprietăţi ale mişcărilor permanente: -Derivatele parţiale în raport cu timpul ale vitezei şi presiunii sunt nule în orice punct
deoarece acestea sunt constante:
0tv=
∂∂r
; 0tp=
∂∂ (3.18)
-Câmpul vitezelor locale este un câmp vectorial fix; liniile de curent formează o familie de curbe fixe în spaţiu; tuburile de curent sunt de asemenea fixe.
-Liniile de curent coincid cu traiectoriile liniile trasoare. -Debitul de greutate, respectiv debitul de masă este constant de a lungul unui tub de
curent(relaţia de continuitate). Mişcările nepermanente (nestaţionare) sunt mişcările la care parametrii locali (v ,p,
etc.) sunt funcţie de coordonate şi timpul t ,la care nu este îndeplinită condiţia de permanenţă. )t,z,y,x(vv rr
= ; p = p(x,y,z,t) (3.19) In cazul mişcărilor nepermanente: -Parametrii locali (viteză, presiune, etc.) nu sunt constanţi.
34

-Câmpul vitezelor locale nu coincide cu traiectoriile particulelor, fiecare particulă găsindu-se pe o linie de curent dată, doar la un singur moment.
-Debitul variază în funcţie de timp. Mişcări permanente uniforme sunt mişcările la care parametrii locali sunt constanţi,
iar liniile de curent sunt rectilinii şi paralele, de exemplu un canal cu secţiune şi pantă constantă. Dacă vitezele locale sunt constante pe liniile de curent mişcarea se numeşte omogen-
uniformă. La mişcările uniforme, într-o secţiune transversală normală pe liniile de curent
presiunile variază după legea hidrostaticii. Mişcări permanente variate (neuniforme) sunt mişcări cu debit constant prin conducte
sau canale cu secţiune sau pantă variabilă în spaţiu, prin orificii, deversoare, remuuri, la debite constante în timp.
Mişcări nepermanente uniforme sunt mişcări la care debitul este variabil cu timpul în conducte, sau canale, cu secţiune constantă.
Mişcări nepermanente variate (neuniforme) sunt mişcări la care debitul variază cu timpul şi secţiunea cu spaţiul, de exemplu scurgerea într-un râu, canal în care se produc remuuri, salturi hidraulice şi alte schimbări de regim ale scurgerii.
Fig.3.6. Mişcări uniforme şi variate.
Când distribuţia în secţiune a parametrilor locali, variază lent de a lungul curentului, pe
porţiuni scurte de albie, curgerea poate fi asimilată cu o curgere cu linii de curent rectilinii şi paralele, mişcarea numindu-se gradual variată (mişcare cu neuniformitate spaţială redusă), iar când variaţia este mare, mişcarea se numeşte rapid variată (mişcare cu neuniformitate spaţială pronunţată), ca de exemplu cazul lamei deversante la un baraj.
3.1.2.3. MIŞCĂRI TRIDIMENSIONALE; BIDIMENSIONALE ŞI UNIDIMENSIONALE. Mişcările tridimensionale sau spaţiale sunt cele la care parametrii locali depind de
cele trei variabile spaţiale x,y,z. )t,z,y,x(vv rr
= ; p = p(x,y,z,t) (3.20) In realitate mişcările lichidelor au caracter spaţial. Mişcările bidimensionale sunt cele la care una din cele trei direcţii poate fi neglijată.
In această categorie se încadrează mişcările plane (în plane paralele cu un plan dat), de exemplu mişcarea permanent uniformă într-o albie prismatică dreptunghiulară foarte lată (cu excepţia zonelor din apropierea malurilor) şi mişcările axial-simetrice care au proprietatea de simetrie în raport cu un ax, de exemplu cazul unei conducte circulare cilindrice.
35

Mişcările unidimensionale la care parametrii locali sunt exprimaţi printr-o singură variabilă spaţială.
Acesta este modelul matematic cel mai utilizat pentru studiul mişcării lichidelor din conducte şi albii deschise.
3.1.2.4. ALTE TIPURI DE MIŞCĂRI. Mişcări sub presiune care se produc în spaţii cu pereţi solizi, ocupate complect cu
lichid, curgerea având loc sub o presiune mai mare ca cea atmosferică. Mişcări cu suprafaţă liberă la care lichidul nu ocupă complet spaţiul disponibil pentru
deplasare, iar curentul prezintă o suprafaţă de contact cu atmosfera sau alt gaz, de exemplu albia unui râu, conductă umplută parţial.
Jeturi de lichid sunt mişcările la care masa de lichid în mişcare este limitată de un fluid de aceiaşi natură sau diferit, fiind un curent de lichid bine individualizat, de exemplu lama deversantă la un baraj.
Mişcări laminare sunt cele la care liniile de curent sunt paralele cu vectorii vitezelor particulelor şi cu direcţia de deplasare a curentului.
Mişcarea se efectuiază în straturi suprapuse fără amestec de substanţă între ele. Traiectoriile şi liniile de curent coincid, sunt paralele şi continui. Mişcarea laminară se numeşte şi mişcare în regim regulat sau mişcare în regim
Poiseuille. Mişcări turbulente sunt cele la care particulele de lichid nu-şi mai păstrează
individualitatea, ele existând numai ca forme instantanee, care se dispersează continuu în masa curentului.
Mişcarea este dezordonată şi întâmplătoare, traiectoriile ne având o formă regulată. Mişcările turbulente se numesc şi mişcări în regim hidraulic.
3.1.3. SISTEME DE REPREZENTARE A MIŞCĂRII LICHIDELOR 3.1.3.1. SISTEMUL DE REPREZENTARE LAGRANGE. Acest sistem studiază mişcarea fiecărei particule de fluid raportate la un sistem de
referinţă fix Oxyz, adică mişcarea fiecărei particule în lungul traiectoriei proprii, începând de la un punct iniţial M(xo,yo,zo,to)(fig.3.6.).
Pentru descrierea mişcării masei de lichid ce conţine n particule este evident că trebuie scrise un număr de n ecuaţii.
Fig.3.7. Mişcarea masei de lichid în sistem Lagrange
Fig.3.8. Mişcarea masei de lichid în sistem Euler
36

In acest sistem variabilele sunt prin definiţie ataşate particulelor de de lichid. Variabilele independente sunt timpul t şi coordonatele iniţiale xo,yo,zo, aferente timpului
iniţial to, numite variabilele lui Lagrange. Ceilalţi parametrii sunt variabile dependente: -Coordonatele particulei x.y.z. în momentul t. respectiv:
x = x(xo,yo,zo,t) ; y = y(xo,yo,zo,t) ; z = z(xo,yo,zo,t) (3.21) care sunt ecuaţiile parametrice ale traiectoriei particulei. -Viteza particulei în momentul t, având componentele:
tzv;
tyv;
txv zyx ∂
∂=
∂∂
=∂∂
= (3.22)
-Acceleraîia particulei în momentul t, având componentele:
2
2z
z2
2y
y2
2x
x tz
tva;
ty
tv
a;tx
tv
a∂∂
=∂∂
=∂∂
=∂
∂=
∂∂
=∂∂
= (3.23)
-Presiunea în punctul M la momentul t: p = p(xo,yo,zo,t) (3.24)
Vectorii viteză şi acceleratie vr ar după Lagrange sunt vectori caracteristici particulei mobile, numiţi vectori substanţiali.
Sistemul Lagrange se pretează numai la calcule hidrodinamice teoretice. 3.1.3.2. SISTEMUL DE REPREZENTARE EULER. In sistemul Euler, mărimile fizice, care descriu mişcarea lichidelor nu mai sunt ataşate
particulelor de lichid.. Sistemul Euler determină elementele mişcării tuturor particulelor care trec printr-un
punct fix din spaţiu, prin componentele sale x,y,z, la un triedru fix, când timpul variază. Pentru descrierea mişcării este necesar să se cunoască vitezele în toate punctele spaţiului şi pentru toţi timpii (fig.3.7).
Variabilele independente sunt timpul t şi coordonatele x,y,z, ale punctelor fixe din domeniul lichidului, de exemplu M1(x1,y1,z1), M2(x2,y2,z2), M(x3,y3,z3) (fig.3.7).
Variabilele dependente se exprimă în acest caz, ca funcţii de punct, definind pentru fiecare mărime un câmp scalar sau un câmp vectorial, după natura mărimii respective.
Viteza locală )v( r este vectorul viteză ataşat punctului M fix din spaţiu şi este egală cu viteza particulei care se află în acel punct.
Câmpul vitezelor este dat de relaţiile: vx = vx(x,y,z,t) ; vy = vy(x,y,z,t) ; vz = vz(x,y,z,t) (3.25)
sau )t,z,y,x(vv rr
= (3.26) Acceleraţia locală )a( r este vectorul acceleraţie ataşat punctului M fix din spaţiu. Vectorii viteză şi acceleraţie sunt vectori caracteristici locului sau vectori locali. Pentru determinarea câmpului acceleraţiilor, trebuie să se ţină seama de componentele
vitezei vx,vy,vz, care sunt funcţii de coordonate x,y,z, şi de timpul t, iar coordonatele sunt la rândul lor funcţii de timp, ceea ce impune utilizarea regulii de diferenţiere totală a unei funcţii de mai multe variabile:
dzzvdy
yvdx
xvdt
tvvd
∂∂
+∂∂
+∂∂
+∂∂
=rrrr
r (3.27)
)dxzvdy
yvdx
xvdt
tv(
dt1
dtvda
∂∂
+∂∂
+∂∂
+∂∂
==rrrrr
r (3.28)
Dar dx = v dt ; dy = vydt ; dz = vzdt (3.29) x
Deci zyx vzvv
yvv
xv
tv
dtvda
∂∂
+∂∂
+∂∂
+∂∂
==rrrrr
r (3.30)
Componentele acceleraţiei pe cele trei axe de coordonate sunt: 37

zx
yx
xxxx
x vzv
vyv
vxv
tv
dtdv
a∂∂
+∂∂
+∂∂
+∂∂
==
zy
yy
xyyv
y vz
vv
yv
vxv
tv
dtdv
a∂
∂+
∂
∂+
∂
∂+
∂
∂== (3.31)
zz
zz
xzzz
z vzv
vyv
vxv
tv
dtdv
a∂∂
+∂∂
+∂∂
+∂∂
==
Derivatele t
v;t
v;
tv zyx
∂∂
∂
∂
∂∂
se numesc derivate locale, deoarece reprezintă intensitatea
de variaţie a vitezei într-un acelaşi punct. Se constată că acceleraţia totală ar este formată din două componente:
-acceleraţia locală: tval ∂∂
=r
r (3.32)
-acceleraţia convectivă(sau de antrenament): zyxc vzvv
yvv
xva
∂∂
+∂∂
+∂∂
=rrr
r (3.33)
Acceleraţia locală rezultă din variaţia în timp a vitezei în puncte fixe din spaţiu şi este caracteristică mişcării nepermanente. Simbolul de derivare parţială arată că în calculul acceleraţiei locale coordonatele punctelor sunt considerate invariabile.
Acceleraţia convectivă este rezultatul vitezelor diferite la diferite puncte ale spaţiului, deci acceleraţia convectivă şi prin urmare acceleraţia totală într-o curgere permanentă nu este în general nulă. Acceleraţia convectivă este egală cu zero în cazul particular al unui câmp omogen al vitezelor, în care viteza este aceiaşi în toate punctele spaţiului.
Presiunea în punctul M este: p = p(x,y,z,t) (3.34)
Sistemul Euler este mai simplu deoarece utilizează teoria câmpului. 3.2.ECUAŢIILE DE MIŞCARE A LICHIDELOR PERFECTE. 3.2.1. PARAMETRII MIŞCĂRII LICHIDELOR PERFECTE. Mişcarea unui lichid este mai complicată faţă de mişcarea unui solid. Mişcarea unui
solid se descompune în fiecare moment într-o translaţie şi o rotaţie în jurul axei instantanee de rotaţie. In mişcarea unui fluid fiecare particulă în mişcare are o translaţie, o rotaţie şi o deformaţie.
Starea unui lichid este complet determinată cinematic şi dinamic, dacă în orice punct din masa lichidului şi în orice moment se cunosc următorii trei parametri:
-Viteza reprezentată de vectorul )t,z,y,x(vv rr
= (3.35) având componentele:
vx = vx(x,y,z,t) ; vy = vy(x,y,z,t) ; vz = vz(x,y,z,t) (3.36) -Presiunea p = p(x,y,z,t) (3.37) -Densitatea ρ = ρ(x,y,z,t) (3.38) Din relaţiile (3.36), (3.37) şi (3.38) rezultă că pentru determinarea mişcării unei
particule de lichid, în cazul cel mai general, trebuie cunoscute următoarele cinci necunoscute vx, vy, vz, p, ρ.
Aceste cinci necunoscute se determină cu ajutorul a următoarelor cinci ecuaţii: -Trei ecuaţii de proiecţii(ecuaţiile lui Euler). -O ecuaţie de condiţie (ecuaţia fizică a lichidului). -O ecuaţie pur cinematică (ecuaţia de continuitate)
38

3.2.2. ECHILIBRUL HIDRODINAMIC. ECUAŢIILE LUI EULER. Fie o particulă de lichid, de formă paralelipipedică de dimensiuni dx,dy,dz, de masă
elementară dm şi densitate ρ, în jurul unui punct M ( fig.3.9).
Fig.3.9. Forţele masice şi forţele de presiune.
Asupra particulei de lichid perfect acţionează: -Forţele masice de rezultantă R
r:
dxdydzfdVfdmfR ρρrrrr
=== (3.39) având componentele:
Rx = fxρdxdydz ; Ry = fyρdxdydz ; Rz = fzρdxdydz (3.40) -Forţele de presiune (de contact,sau de legătură)) exercitate asupra faţetelor particulei
de lichidul înconjurător:
Px = pdydz – (p + )dxxp∂∂ dzdy = dxdzdy
xp∂∂
−
Py = pdzdx – (p + )dyyp∂∂ dzdx =-- dxdydz
yp∂∂ (3.41)
Pz = pdxdy – (p + )dzzp∂∂ dxdy = -
zp∂∂ dxdydz
Lichidul fiind perfect forţele de frecare şi forţele de compresibilitate sunt se consideră nule.
Conform principiului lui d’Alembert : forţele de inerţie ( ar dm) echilibrează în orice moment rezultanta fortelor active ( R
r)şi a forţelor de legătură ( P
r), rezultă :
PRdmdtvddma
rrrr
+== (3.42)
Proiecţiile relaţiei (3.42) pe axele de coordonate sunt:
axdm = Rx + Px ; aydm = Ry + Py ; az = Rz + Pz (3.43) Introducând în relaţiile (3..43) relaţiile (3.40) şi (3.41) se obţine:
)dt
dvf(
xp x
x −=∂∂ ρ
)dt
dvf(
yp y
y −=∂∂ ρ (3.44)
39

)dt
dvf(zp z
z −=∂∂ ρ
relaţii denumite ecuaţiile lui Euler (sau ecuaţiile mişcării ale lui Euler) care exprimă echilibrul dinamic al unei particule de lichid perfect.
Dacă înmulţim relaţiile (3.44) cu versorii sistemului de referinţă ,k,j,irrrşi le adunăm,
obţinem:
zyx fjfif[kzpj
ypi
xp
++=∂∂
+∂∂
+∂∂ rrrrr
ρ )]kdt
dvjdt
dvi
dtdv
(k zyxrrrr
++− (3.45)
sau: = grad p = p∇ (ρ )dtvdfrr
− (3.46)
relaţia ce exprimă echilibrul hidrodinamic sub formă vectorială.
Se vede că în cazul când acceleraţia este nulă, ecuaţiile de mai sus se transformă în ecuaţii de echilibru hidrostatic.
3.2.3. ECUAŢIA DE CONDIŢIE. Ecuaţia de condiţie, denumită şi ecuaţia fizică a lichidelor, este dată de legătura dintre
densitatea ρ, presiunea p şi temperatura to. ρ = ρ(p, to) (3.47) Se admite că densitatea este constantă în fiecare punct şi în fiecare moment, iar
variaţiile de presiune şi temperatură pot fi considerate neglijabile, caz în care ecuaţia de condiţie este:
ρ = constant (3.48) 3.2.4. ECUAŢIA DE CONTINUITATE. Fie un domeniu dintr-un lichid în mişcare, delimitat de un volum elementar
paralelipipedic dV =dxdydz, ale cărui feţe sunt considerate suprafeţe de control (fig.3.10).
Fig.3.10. Variaţia masei lichidului din domeniu.
Pentru lichidul considerat compresibil în mişcare nepermanentă, densitatea ρ şi viteza
sunt funcţii de coordonatele spaţiale x,z,y, si de timpul t. vr
Pentru feţele de control ABCD şi EFGH, în timpul elementar dt, masa din domeniu creşte datorită variaţiei densităţii cu: 40

dxdydzdtt
dxdydzdxdydz)dtt
(∂∂
=−∂∂
+ρρρρ (3.49)
Pentru faţa de control ABCD, în acelaşi interval de timp elemetar, intră cu viteza vx o
masă egală cu ρvxdydzdt, iar prin faţa EFGH iese cu viteza dxxv
v xx ∂
∂+ o masă de lichid egală
cu ]x
)v(v[ x
x ∂∂
+ρ
ρ dydzdt, aşa încât diferenţa dintre masa care intră în domeniu şi care iese ţn
intervalul de timp dt este:
x)v(
dydzdt]dxx
)v(v[dydzdtv xx
xz ∂∂
−=∂
∂+−
ρρρρ dxdydzdt (3.50)
In mod analog pentru feţele normale pe direcţiile Oy şi Oz obşinem:
- dxdydzdty
)v( y
∂
∂ ρ; dxdydzdt
z)v( z
∂∂
−ρ (3.51)
Pentru domeniul considerat diferenţa de masă datorită variaţiei vitezei este:
dxdydzdt]z
)v(y
)v(x
)v([ zyx
∂∂
+∂
∂+
∂∂
−ρρρ
(3.52)
Conform principiului conservării energiei, variaţia masei datorită variaţiei vitezei, trebuie să fie egală cu masa conţinută în volumul elementar paralelipipedic, în unitatea de timp.
Aşa dar din egalitatea relaţiilor (3.49) şi (3.52) rezultă:
0z
)v(y
)v(x
)v(t
zyx =∂
∂+
∂
∂+
∂∂
+∂∂
rrrρρρρ (3.53)
sau: 0)v(t
=∇+∂∂ rρρ (3.54)
Relaţia (3.53) şi (3.54) este ecuaţia de continuitate (ecuaţia de transfer) sub formă diferenţială pentru mişcarea nepermanentă a unui lichid compresibil (densitatea variază în spaţiu şi timp).
Prin aplicarea operatorului vectorial ∇ produsul din paranteza relaţiei (3.54) se poate
scrie: 0v.∇ r.vt
=+∇+∂∂ r ρρρ (3.55)
şi utilizând expresia derivatei substanţiale, obţinem:
0v.dtd
=∇+rρρ (3.56)
Ea arată că într-un sistem închis, fără surse şi pierderi de lichid, masa lichidului care umple sistemul se conservă.
Relaţia (3.53) reprezintă legea generală de conservare a masei: cantitatea de masă care intră, minus cantitatea de masă care iese dintr-un volum, în unitatea de timp, este egală cu variaţia masei lichidului din elementul de volum considerat.
Rezultă deci că lichidul rămâne un element continuu, în tot timpul mişcării, neexistând în interiorul acestuia discontinuităţi sau goluri.
La lichide reale cu mişcări nepermanente cu vârtejuri avem:
0v.dtd
≠∇+rρρ (3.57)
Cazuri particulare: a)Mişcări permanente şi lichide incompresibile, caz în care densitatea ρ=constant în raport cu timpul, deci:
0dtd
=ρ dar 0≠ρ deci divv. =∇
r vr = 0 (3.58)
Din această relaţie rezultă că principiul conservării masei se reduce la principiul conservării volumului. Ecuaţia (3.58) reprezimtă matematic condiţia de deformare nulă. 41

Deasemeni rezultă că în unitatea de timp,volumul de licid care intră în domeniul considerat este egal cu volumul care iese.
b)Mişcări permanente şi lichide compresibile: 0)v.( =∇
rρ (3.59) c)Fir de curent în regim permanent. Pentru un fir de curent dintr-un tub de curent, în care lichidul are densitatea constantă,
ecuaţia de continuitate este: dQ = v1dA1=v2dA2=…=vidA=…= constant (3.60)
vi, sunt vitezele din secţiunile vii dAi (i = 1…n). d) Curent de lichid monodimensional în regim permanent (fig.3.11).
Fig.3.11. Curent de lichid monodimensional. Ecuaţia de continuitate folosită în calculele practice este:
Q = A1V1 =A2V2=…=AiVi=…= constant (3.61) Vi, Ai (i= 1…n) sunt vitezele medii, respectiv suprafeţele udate aferente secţiunilor
curentului Si. 3.2.5.ECUAŢIA GENERALĂ A MIŞCĂRII PERMANENTE. Inmulţind ecuaţiile lui Euler (3.44) dx,dy ,dz, şi le adunăm, obţinem:
ddt
dvdx
dtdv
()fff(dzzpdy
ypdx
xp yx
xyx +−++=∂∂
+∂∂
+∂∂ ρρ y+ )dz
dtdvz (3.62)
Insă: dp = dzzpdy
ypdx
xpdt
tp
∂∂
+∂∂
+∂∂
+∂∂ (3.63)
iar dx/dt = vx ; dy/dt = vy ; dz/dt = vz (3.64) aşa încât relaţia (3.62) devine:
dp - dzfdyfdxf[dttp
zyx ++=∂∂ ρ - (vxdvx+vydvy+vzdvz)] (3.65)
adică: dp - )]2v(ddzfdyfdxf[dt
tp 2
zyx −++=∂∂ ρ (3.66)
care reprezintă ecuaţia generală a mişcării nepermanente pentru un fir de lichid perfect. In cazul mişcării permanente, ecuaţia generală are forma:
dp = )]2v(ddzfdyfdxf[
2
zyx −++ρ (3.67)
deoarece presiunea nu variază cu timpul, .0tp =∂∂ Dacă v = 0, lichidul este în repaus, relaţia (3.67) devine ecuaţia generală diferenţială a
hidrostaticii. 3.2.6.ECUAŢIA LUI DANIEL BERNOULLI. 3.2.6.1.ECUAŢIA LUI BERNOULLI ÎN MIŞCAREA PERMANENTĂ A. LICHIDELOR PERFECTE
42

Să considerăm o particulă de masă egală cu unitatea, care se deplasează pe axa unui fir de curent sub acţiunea câmpului gravitaţional, pe o distanţă elementară ds între punctele M((x,y,z) şi M1(x1,y1,z1), (fig.3.12).
Fig.3.12. Mişcarea pe firul de curent. Aplicând ecuaţia generală a mişcării permanente (3.67):
dp = ρ[fxdx+fzdz+fydx – d( )2v2
] (3.68)
în care: fx = fy = 0 ; fz = -g (3.69)
obţinem: dp + ρgdz + )2v(d
2
ρ = 0 (3.70)
Prin integrarea ecuaţiei (3.70) obţinem:
ttanconsg2
vgpz
2
=++ρ
(3.71)
Relaţia (3.71) este ecuaţia lui Bernoulli şi reprezintă expresia matematică a legii conservării energiei mecanice în lungul unui fir de curent de lichid perfect în regim permanent.
Rezultă că ecuaţia lui Bernoulli, pentru orice punct de pe firul de curent este:
ttanconsg2
vg
pz......
g2v
gpz
g2v
gpz
2nn
n
222
2
211
1 =++==++=++ρρρ
(3.72)
Ecuaţia lui Bernoulli se obţine şi admiţând că forţa unitară masică fr
derivă din potenţialul gravitaţional:
dU = -dV = -gdz (3.73)
)2v(ddz
zUdy
yUdx
xU[dp
2
−∂∂
+∂∂
+∂∂
= ρ (3.74)
dp = )]2v(ddU[
2
−ρ (3.75)
dp + ρg + ρd )2v(
2
= 0 (3.76)
relaţie identică cu relaţia (3.70). 3.2.6.2. REPREZENTAREA GRAFICĂ ŞI INTERPRETAREA ECUAŢIEI LUI BERNOULLI Considerăm un tub de curent elementar, cu două tuburi piezometrice, poziţionat la o
distanţă oarecare de un plan de comparaţie orizontal (fig.3.13).
43

Fig.3.13. Reprezentarea grafică a ecuaţiei lui Bernoulli. a) Interpretarea geometrică.
Se observă că termenii ecuaţiei lui Bernoulli, din punct de vedere dimensional, sunt lungimi. aşa încât ele reprezintă înălţimi denumite şi sarcini. Astfel:
z este sarcina (înălţimea) de poziţie sau geodezică;
gpρ
= γp este sarcina (înălţimea) piezometrică;
g2v2
este sarcina(înălţimea) cinetică
In interpretarea geometrică rezultă că pentru orice punct de pr un fir de curent de lichid perfect aflat în mişcare permanentă, suma sarcinilor (înălţimilor) de poziţie, piezometrică şi cinetică este constantă.
Hg2
vgpz
2
=++ρ
(3.77)
Sarcina p/ρg = p/γ măsoară presiunea unui punct oarecare al firului de curent şi reprezintă înălţimea reală la care s-ar ridica lichidul într-un tub piezometric amplasat în punctul considerat.
Locul geometric al extremităţilor superioare ale înălţimilor p/ρg= p/γ defineşte linia piezometrică.
Cota oricărui punct de pe linia piezometrică, măsurată de la planul de comparaţie,este sarcina potenţială totală Hp, a punctului considerat:
Hp = z + gpρ
(3.78)
Locul geometric al extremităţilor înălţimilor aferente sarcinii cinetice, se numeşte linia de energie.
Hc = g2
v2
(3.79)
Această linie este cuprinsă într-un plan orizontal denumit plan de sarcină hidraulică (PSH) care este paralel la planul de comparaţie (PC) la cota constantă H.
H = Hp + Hc (3.80) Sarcina totală H se numeşte înălţime (cotă) hidraulică sau energia specifică totală a
secţiunii. 44

b) Interpretarea energetică. Dacă înmulţim membrii ecuaţiei lui Bernoulli (3.71) valoarea mg = constant, care
reprezintă greutatea particulei ce se deplasează pe firul de curent, obţinem:
mgz + ρ
mp + 2
mv2
= constant (3.81)
unde mgz = energia potenţială de poziţie a particulei; mp/ρ=energia pοtenţială de presiune a particulei; mv2 /2= energia cinetică a particulei, aşa încât (m = 1):
z este energia specifică potenţială de poziţie;
gpρ
= γp este energia specifică de presiune;
g2v2
este energia specifică cinetică.
Rezultă că pentru orice punct de pe un fir de curent de lichid perfect aflat în mişcare permanentă, suma energiilor specifice de poziţie, de presiune şi cinetică este constantă.
c) Interpretarea mecanică. Termenii ecuaţiei lui Bernoulli, din punct de vedere mecanic, reprezintă lucruri
mecanice. raportate la greutatea particulei, conform teoremei echivalenţei dintre lucrul mecanic al forţelor exterioare şi interioare, şi variaţia energiei cinetice.
3.2.6.3.ECUATIA LUI BERNOULLI ÎN MIŞCAREA PERMANENTĂ A
LICHIDELOR INCOMPRESIBILE REALE,
In cazul unui fir de curent de lichid real (vâscos), energia specifică totală în lungul firului de curent, nu mai este constantă, aceasta scăzând pe parcurs datorită eforturilor tangenţiale
Fig.3.14. Reprezentarea grafică a ecuaţiei lui Bernoulli la lichide reale.
Pentru lichide reale, ecuaţia lui Bernoulli are forma:
21r
222
2
211
1 hg2
vg
pzg2
vg
pz −+++=++ρρ
(3.82)
45

Dacă înmulţim relaţia (3.82) mg = constant, observăm că mghr1-2 reprezintă energia disipată (pierdută) între punctele 1 şi 2, datorită rezistenţei vâscoase a lichidului real, energia hidraulică disipată se regăseşte sub formă de energie termică.
In consecinţă din punct de vedere energetic hr1-2 este energia specifică disipată între secţiunile 1-2; din punct de vedere mecanic hr1-2 este lucrul mecanic consumat pentru învingerea rezistenţelor datorate eforturilor tangenţiale de viscozitate; din punct de vedere geometric hr1-2 este înălţimea care măsoară pierderile de sarcină între secţiunile considerate.
hr1-2 = H1 – H2 (3.83) Se vede că linia de energie nu mai este orizontală şi cuprinsă în planul de sarcină, ca în
cazul firului de curent de lichid perfect, ci este continuu descrescătoare datorită pierderilor de sarcină care se cumulează în sensul curgerii, înălţimile (cotele) hidraulice micşorându-se (H1>H2).
3.2.6.4. COEFICIENTUL LUI CORIOLIS. S-a arătat că într-un curent de lichid vitezele locale ale particulelor diferă. Considerăm o particulă elementară de masă dm care se află într-un punct M şi are
viteza locală v. Energia specifică cinetică e a particulei raportată la greutate (respectiv pentru unitatea
de greutate) este:
g2v
gdm
dmv21
e2
2
== (3.84)
Considerăm în jurul punctului M secţiunea elementară de arie dA, prin care trece debitul de greutate al tubului elementar de curent este:
dQ = γvdA (3.85) Fluxul elementar de energie cinetică dE prin tubul elementar de curent este:
dE = eγvdA = dAg2
v3
γ (3.86)
Fluxul de energie cinetică prin secţiunea punctului M este:
dAg2
vEA
3
∫= γ (3.87)
Conform modelului adoptat, în locul vitezelor locale, trebuie să apară viteza medie V a curentului din secţiunea considerată. In acest scop viteza locală se exprimă prin relaţia:
v = k(M) (3.88) unde k(M) este coeficientul de distribuţie al vitezei locale în secţiunea punctului M.
Deci: E = dA)M(kA1
g2VAVdA)M(k
g2v
A
3
A
23
3
∫∫ = γγ = Qg2
V 2αγ (3.89)
deoarece conform relaţiei de continuitate A1V1=A2V2=….= AV = Q, iar cu α s-a notat:
∫=A
3 dA)M(kA1α (3.90)
denumit Coeficientul lui Coriolis, care este întotdeauna supraunitar 1≥α . Coeficientul lui Coriolis, poate fi dedus şi prin compararea sarcinii cinetice reale,
calculată cu vitezele locale v ale curentului pentru o secţiune de arie A, cu sarcina cinetică fictivă a curentului calculată cu viteza medie V = Q/A, ce trece prin aceiaşi secţiune:
g2V
g2v
.........g2
vg2
v(n1 22
n22
21 α=+++ (3.91)
46

Coeficientul lui Coriolis α Tabela 3.1.
Specificaţie Minim Mediu Maxim-Albii prismatice sau cu neuniformitate spaţială redusă şi pentru deversoare 1,10 1,15 1,20 -Cursuri de ape torenţiale 1,15 1,30 1,50 -Mişcare uniformă a lichidelor perfecte - 1,00 - -Mişcare turbulentă > 1 - < 2 -Mişcare laminară în conducte cilindrice - 2,00 - -Mişcări cu viteze foarte neuniform distribuite - > 2,0 -
3.2.6.5. ECUAŢIA LUI BERNOULLI PENTRU CURENŢI DE LICHID REAL
CU SECŢIUNE FINITĂ In cazul curenţilor de lichid real, de secţiune finită, incluşi într-un tub de curent de
curent de secţiune finită, vitezele locale într-o secţiune transversală sunt neuniform distribuite. Ecuaţia lui Bernoulli se poate scrie pe o linie de curent convenabil aleasă, pe care
lichidul ar avea vitezele egale cu vitezele medii în secţiunile transversale ale curentului, dacă sarcina cinetică se corectează cu coeficientul lui Coriolis α, care ţine seama de neuniformitatea distribuţiei vitezelor într-o secţiune în cazul mişcării laminare.
a) Ecuaţia lui Bernoulli pentru curgere sub presiune. Pentru curgerile sub presiune în regim permanent, ecuaţia lui Bernoulli pentru curent cu
mişcare uniformă (fig.3.15.a) şi pentru curent cu mişcare gradual variată (fig.3.15.b), are forma: J=panta hidraulică; I=panta piezometrică; I=panta geodezică
Fig.3.15. Reprezentarea grafică a ecuaţiei lui Bernoulli pentru curgere sub presiune
a)Mişcare uniformă. b)Mişcare gradual variată 47

21r
2222
2
2111
1 hg2Vpz
g2Vpz −+++=++
αγ
αγ
(3.92)
b) Ecuaţia lui Bernoulli pentru curgere cu suprafaţă liberă. In cazul mişcării uniforme cu suprafaţă liberă (fig.3.16) α1=α2=α, iar panta hidraulică,
piezometrică şi geodezică sunt egale (J=I=i), aşa încât linia de energie, linia piezometrică şi linia fndului albiei sunt paralele.
Fig.3.16. Reprezentarea grafică a ecuaţiei lui Bernoulli pentru mişcare uniformă.
z + h + g2
V 2α = h + g2
V 2α + hr1-2 (.3.94)
de unde: z = hr1-2 (3.95) In cazul mişcării gradual variate cu suprafaţă liberă (fig.3.17), ecuaţia lui Bernoulli este:
Fig.3.17. Reprezentarea grafică a ecuaţiei lui Bernoulli pentru mişcare gradual variată.
21r
222
2
211
1 hg2Vh
g2Vhz −++=++
αα (3.96)
3.2.6.6. PANTA HIDRAULICĂ, PIEZOMETRICĂ, GEODEZICĂ. a)Panta hidraulică. Panta hidraulică pentru mişcarea uniformă este dată de expresia:
48

LHHJ 21 −= (3.97)
Panta hidraulică pentru mişcarea gradual variată are expresia:
dLdHJ −= (3.98)
Semnul minus apare datorită faptului că linia de energie este continuu descrescătoare. b)Panta piezometrică Panta piezometrică pentru mişcare uniformă este:
LHH
I 2p1p −= (3.99)
Panta piezometrică pentru mişcare gradual variată este
dLdH
I p±= (3.100)
Semnul arată că linia piezometrică poate fi crescătoare sau descrescătoare, după cum presiunea creşte sau scade, debitul fiind însă constant..
±
c)Panta geodezică este:
Lzzi 21 −= (3.101)
3.2.6.7. PERDEREA DE SARCINĂ ÎN MIŞCAREA PERMANENTĂ. Considerăm mişcarea lichidului uniformă sau gradual variată, în model
unidimensional, luând în calcule viteza medie V. Pierderea de sarcină este egală cu consumul de energie mecanică a unităţii de greutate
de lichid, când acesta parcurge o distanţă L. Pierderea de sarcină hr are două componente: a)Pierderea de sarcină liniară hd, -datorată rezistenţelor hidraulice(vâscozitatea) care
se manifestă în lungul curentului în mişcare uniformă şi este proporţională cu distanţa L respectiv lungimea curentului:
hd = J.L (3.102) unde J este panta hidraulică.
Pierderea de sarcină liniară se exprimă şi prin relaţia:
g2Vh
2
dd ξ= (3.103)
unde dξ este coeficientul de pierdere de sarcină liniară (adimensional). Pentru albii deschise acest coeficient este:
RL
d λξ = (3.104)
unde: λ = coeficient care depinde re rugozitatea albiei; L = lungimea drumului parcurs; R = raza hidraulică a suprafeţei udate.
b)Pierderea de sarcină locală hl –se datorează rezistenţelor locale în zonele cu neuniformităţi care stânjenesc mişcarea, cum sunt de exemplu: coturile, pragurile, îngustările sau lărgirile bruşte, etc.
g2Vh
2
ll ξ= (3.105)
unde lξ = coeficientul rezistenţelor locale sau coeficientul de pierdere de sarcină locală (adimensional).
Din relaţia (3.105) rezultă că lξ este egal cu raportul dintre pierderea de sarcină locală şi înălţimea cinetică.
49

In proiectare se folosesc valorile lξ = 0,05….0,5. Pierderea de sarcină totală sau pierderea totală de energie între două secţiuni ale
curentului este egală suma pierderilor de sarcini liniare cu cele locale: hr = hd + hl (3.106)
Fluxul de energie disipată prin pierderile de sarcină pe lungimea L este: Er = γ.Q.hr1-2 (3.107)
3.2.6.8. BILANŢUL ENERGETIC ÎN MIŞCAREA PERMANENTA. In mişcarea permanentă, energia mecanică a masei de lichid care se află între secţiunile
1-1 şi 2-2, este constantă în timp, deoarece parametrii în care se exprimă ea în sistemul Euler, nu sunt funcţii de timp.
Fluxul (debitul) de energie E1 intră în domeniul considerat prin secţiunea 1-1, este egal cu cel care iese prin secţiunea 2-2.
Fluxul de energie care iese din secţiunea 2-2, este format din: -Fluxul de energie purtat de particulele care ies din secţiunea 2-2, notat cu E2. -Fluxul de energie disipat (risipit), datorită pierderii de sarcină, notat cu Er. Intre cele trei fluxuri există următoarea relaţie de bilanţ enrgetic:
E1 = E2 + Er (3.108) care rezultă din aplicarea din aplicare legii conservării energiei.
Dar, E1 = Ep1 + Ec1; E2 = Ep2 + Ec (3.109) aşa încât: Ep1 + Ec1 = Ep2 + Ec2 + Er (3.110)
unde: Ep = )pz(Qγ
γ + este fluxul de energie potenţială
Ec = g2
VQ2αγ este fluxul de energie cinetică
Er = γQhr1-2 este fluxul de energie disipată, Relaţia (3.110) devine:
21r
2222
2111
1 Qhg2VQ)pz(Q
g22VQ)pz(Q −+++=++ γ
αγ
γγ
αγ
γγ (3.111)
Simplificând relaţia (3,111) cu γQ se obţine ecuaţia lui Bernoulli pentru lichide reale. 3.2.6.9. ECUAŢIA LUI BERNOULLI PENTRU UN CURENT CURBAT.
ÎN PLAN VERTICAL In cazul mişcării unui curent de lichid curbat în plan vertical, ecuaţia lui Bernoulli nu
poate fi aplicată, decât dacă se corectează termenii de energie potenţială. Una din corecţii este:
Fig.3.18. Distribuţia presiunii hidrostatice la curenţi curbaţi.
50

)pz(H p γββ += (3.112)
unde β este un coeficient care ţine seama de abaterea distribuţiei presiunilor de le legea hidrostaticii (distribuţie liniară) (fig.3.18).
3.2.6.10. PRESIUNEA DE IMPACT. Considerăm un obstacol situat într-un curent de lichid în mişcare permanentă (fig.3.19). Pentru cele două puncte 1 şi 2 pe un fir de curent normal la bordul de atac (impact) al
curentului, ecuaţia lui Bernoulli, pentru v2 = 0, este.
γγ2
2
211
1pz
g2vpz +=++ (3.113)
Fig.3.19. Presiunea de impact. Considerând că z1 z2 rezultă că: ≈
p1 - p2 + 0g2
v21 =γ (3.114)
unde: i
21 pg2
v=γ este presiunea de impact sau presiunea de stagnare.
Din relaţia (3.114) rezultă că: pi = p2 - p1 (3.115)
adică presiunea de impact pi este egală cu diferenţa dintre presiunea totală p2 exercitată pe bordul de atac şi presiunea statică p1 din amonte, care nu este influenţată de obstacol.
3.2.7. TEOREMA IMPULSULUI: Din mecanica solidului se cunoaşte că derivata impulsului (cantităţii de mişcare) în
raport cu timpul este egală cu suma vectorială a forţelor exterioare:
∑= eF)vm(dtd rr sau ∑= dtF)vm(d e
rr (3.116)
Fig.3.20. Mişcarea lichidului printr-un tub.
51

Considerăm un lichid incompresibil în mişcare permanentă printr-un tub cu secţiunile A1 şi A2 cărora le corespund presiunile p1 şi p2 şi forţele de presiune P1=p1A1 şi P2=p2A21nr 2nr
(fig.3.20). Dacă notăm cu G greutatea lichidului din tub şi cu
rRr
rezultanta reacţiunilor exercitate de pereţii tubului asupra lichidului, aplicând relaţia (3.116), obţinem în câmpul gravitaţional:
∑=+++= e21 FPPRG)vm(dtd rrrrrr (3.117)
Prin integrare în intervalul de timp egal cu unitatea (t = 1), în care impulsul variază de la la : 1vmr 2vmr
dt)F()vm(d2
1
v
v
1
0 e∫ ∫ ∑=rr (3.118)
de unde: ∑=− e12 F)vv(mrrr (3.119)
Pentru t = 1 avem: QQg
m ργ== (3.120)
Deci relaţia (3.119) devine ∑=+++=− e2112 FPPRG)vv(Q
rrrrrrrρ (3.121) Rezultă că: variaţia în unitatea de timp a impulsului (cantităţii de mişcare) este egală
cu suma vectorială a forţelor exterioare. Prin proiecţia relaţiei (3.121) pe un sistem de referinţă ortogonal se obţin trei relaţii
analitice. 4. SCURGEREA PERMANENTĂ PE ALBII DESCHISE. 4.1. GENERALITĂŢI. 4.1.1.DEFINIŢIE. Sistemele hidraulice în cuprinsul cărora lichidul se scurge în condiţiile curenţilor cu
suprafaţă liberă, se numesc albii deschise. În această categorie intră păraiele, torenţii, râurile, fluviile, canalele, conductele cu
secţiunea parţial plină, etc. 4.1.2. CLASIFICAREA ALBIILOR DESCHISE. Albiile deschise se pot clasifica după diverse criterii. De exemplu: a)După originea lor: -Albii naturale, rezultate din fenomenele de eroziune, sau alte fenomene cum sunt:
rigolele, păraiele, torenţii, râurile, fluviile, cursurile de ape subterane cu suprafaţă liberă. -Albii artificiale, care sunt construite în diverse scopuri, cum sunt: canalele de navigaţie,
canalele de regularizare a cursurilor de apă (râuri, păraiie, torenţi). b)După variaţia secţiunii transversale: -Albii prismatice, la care suprafaţa udată A variază exclusiv în funcţie de adâncimea
curentului h, fiind definite de relaţia: A = f(h) (4.1)
-Albii neprismatice, la care variaţia suprafeţei udate este funcţie de adâncimea curentului h, şi lungimea curentului L, definite hidraulic prin relaţia:
A = f(h,L) (4.2) c)După felul mişcării:
52

-Albii cu mişcări uniforme, la care liniile de curent sunt rectilinii şi paralele, viteza medie şi adâncimea sunt constante, iar evident suprafaţa liberă este un plan înclinat.
-Albii cu mişcări neuniforme, la care nu sunt îndeplinite condiţiile pentru mişcarea uniformă.
Mişcările neuniforme pot fi: -Mişcări gradual variate-la care liniile de curent sunt aproximativ rectilinii şi paralele,
deci apropiate de mişcarea uniformă. Mişcarea gradual variată poate fi lentă sau rapidă. -Mişcări rapid variate, care au neuniformităţi mari în variaţia vitezelor şi al liniilor de
curent. De exemplu mişcarea peste trepte, praguri, deversoare,etc. -Saltul hidraulic, face trecerea de la mişcarea rapidă la mişcarea lentă. Scurgerile cu suprafaţă liberă pot antrena şi aerul, mai ales la viteze mari. Mişcarea uniformă presupune următorii parametri constanţi în lungul curentului: forma
secţiunii transversale, panta, axa albiei rectilinie, rugozitatea pereţilor albiei, debitul. Deoarece albiile naturale nu se încadrează în aceste condiţii, în ipoteza regimului
permanent uniform, în calcul se pot considera sectoare scurte de albie-cel mult câteva sute de metri-pe un interval în care debitul se menţine în jurul unei valori maxime.
4.2. PARAMETRII MIŞCĂRII PERMANENTE UNIFORME DIN ALBII. 4.2.1. PARAMETRII GEOMETRICI AI ALBIEI. Secţiunea transversală a unei albii este secţiunea normală la direcţia generală de
mişcare a curentului considerat unidimensional (secţiunea D’E din figura 4.1).
Fig.4.1. Secţiune longitudinală.
Deoarece panta longitudinală este mică, se foloseşte secţiunea verticală DE, pentru că
DE=h/cosθ iar cosθ 1≈ , cele două secţiuni coincid. Parametrii geometrici ai secţiunii transversale sunt (fig.4.2)
Fig.4.2. Secţiuni transversale.
H-adâncimea curentului B -lăţimea curentului la suprafaţa liberă P -perimetrul udat A -suprafaţa udată
53

PAR = -raza hidraulică
BAhm = -adâncimea hidraulică
Pentru secţiunile transversale trapezoidale şi triunghiulare se folosesc: m =ctgα -coeficientul de taluz al canalului m’= αctg1+ -coeficientul second de taluz
Parametrii secţiunilor transversale trapezoidale (fig.4.2.a) se pot exprima şi prin următoarele mărimi adimensionale:
hb
=β -lăţimea relativă a albiei
bh1
=β
-adâncimea relativă a albiei.
Pentru albiile ale căror secţiuni au forme neregulate, pentru calculul acestor parametri, secţiunea se împarte în forme geometrice cunoscute (fig.4.2.b).
Profilul longitudinal pentru un curent de lungime L în cazul mişcării uniforme, este dreapta de pantă geodezică i :
i = θθ sinL
zztg 21 ≈−
= = J = I (4.3)
deoarece panta hidraulică, panta piezometrică şi panta geodezică sunt egale ca mărime. 4.2.2.DISTRIBUŢIA PRESIUNILOR. In cazul curgerii rectilinii şi paralele, într-o secţiune transversală a unui curent continuu,
presiunea hidrostatică se distribuie după legea hidrostaticii. Pentru pante mici (θ 6ο), se neglijează perturbaţiile turbulenţei, aşa încât presiunea
variază liniar cu adâncimea curentului. ≤
Dacă panta albiei este mai mare (θ > 6o), în calculul înălţimilor piezometrice, se introduce un factor de corecţie care ţine seama de influenţa pantei, şi care este cos2θ. Cu acest factor se multiplică adâncimea măsurată pe verticală.
4.2.3. VITEZELE CURENTULUI. 4.2.3.1. FORMULA LUI CHEZY PENTRU VITEZA MEDIE. Considerăm un tronson de albie de lungime L, cu pantă, secţiune transversală şi
rugozitate constantă. Care este delimitată de două secţiuni normale pe direcţia de mişcare a unui curent uniform (fig.4.3).
Pentru studiul rezistenţelor pe un tronson de albie se ia în calcul viteza medie V.
54

Fig.4.3. Tronsonul de albie şi forţele aferente.
Greutatea proprie a tronsonului G se descompune într-o componentă Gsinθ şi Gcosθ.
Forţei Gsinθ care pune în mişcare lichidul I se opune forţa de frecare T. Presiunile P1 şi P2 fiind egale şi de sens contrar se anulează, aşa încât ecuaţia de echilibru este:
T = Gsinθ (4.4) Chézy a admis că forţa de frecare T este proporţională cu perimetrul udat P, viteza
medie V la patrat şi cu greutatea specifică a lichidului γ. Pentru un tronson de lungime unitară L = 1, forţa de frecare T este:
22 PV
C1T γ= (4.5)
C este coeficientul de viteză (Chézy), care se exprimă în m0,5s-1 valabil pentru ape limpezi, considerat constant.
Greutatea tronsonului de lichid pe lungimea L este G = γAL, A fiind suprafaţa udată. Pentru L = 1 lichidului este:
G1 = γA (4.6) Ecuaţia de echilibru (4.4) devine:
2C1 γPV2 = γAsinθ (4.7)
Dar sinθ ≈ tgθ = J = I = I (4.8)
şi RPA= ( raza hidraulică) (4.9)
obţinem: == RJCV C RiCRI = (4.10) care este formula lui Chézy pentru calculul vitezei medii a curentului.
Viiturile torenţiale antrenează cantităţi mari de aluviuni, pentru transportul cărora, se consumă o mare cantitate de energie cinetică. In acest context viteza medie de scurgere se micşorează în comparaţie cu cea a apei limpezi, fapt ce implică corectarea coeficientului de viteză C cu un coeficient subunitar K<1 denumit coeficient de torenţialitate.
Coeficientul de torenţialitate rezultă din aplicarea principiului consevării impulsului (cantităţii de mişcare):
gγ QVl = [ p
p V]g
gγγ
ηγ −+ (4.11)
55
unde membrul din stânga egalităţii este impulsul curentului de apă limpede (γ, Vl), iar cel din dreapta egalităţii este impulsul curentului bifazic=apă+aluviuni(pământ γp, Vp).

Coeficientul de încărcare al curentului cu aluviuni (pământ) η , este raportul dintre volumul de aluviuni transportate (debitul volumetric al materialelor transportate-m3/s) şi volumul de apă care le transportă (debitul curentului –m3s-1) la unitate.
In practică se ia : .4,0.....2,0=η Din relaţia (4.11) rezultă:
1)(V
VK
epl
p <=−+
==γγ
γγηγγ (4.12)
unde numitorul este greutatea specifică echivalentă γε a lichidului bifazic (apă+alviuni).
Astfel viteza medie a curentului de apă încărcat cu aluviuni Va este: Va = KC Ri (4.13)
4.2.3.2. COEFICIENTUL DE VITEZĂ C. Pe baza unor observaţii, exeperimentări în laboratoare şi natură s-au stabilit formule
empirice de calcul pentru coeficientul de viteză (Chézy) care depăşesc numărul de 140. Aceste formule sunt mai mult sau mai puţin aproximative, funcţie de condiţiile specifice. Totuşi pentru calcule orientative sunt folositoare. Este evident că pentru calcule exacte, se folosesc metodele corespunzătoare ca măsurători directe, cercetări în laboratoare, etc.
Formulele utilizate în proiectare se grupează în formule exponenţiale şi formule neexponenţiale.
a)Formule exponenţiale.
1. Formula lui R.Manning (1890), pentru R < 1 m 6/1Rn1C = (4.14)
2. Formula lui Forchheimer (1923), pentru m1R ≥ 5/1Rn1C = (4.15)
3. Formula lui Pavlovski (1925) yRn1C = (4.16)
unde y = 2,5 R)10,0n(75,013,0n −−− pentru 0,10 m0,3R ≤≤ (4.17) In aceste relaţii n = coeficientul de rugozitate, R = raza hidraulică.
Coeficientul de rugozitate n (din C.Mateescu 1963)
Tabela 4.1. Nr crt. Natura pereţilor canalului sau a conductei n 5%) ±( 1/n( %)5±
0 1 2 3 1 2 3 4 5 6 7 8 9 10 11 12 13
Dulapi negeluiţi aşezaţi în lung Dulapi negeluiţi aşezaţi transversal Beton netencuit execuţie bună Beton tencuit,ciment sclivisit,executat îngrijit Pereuri de beton spoit cu lapte de ciment Piatra brută rostuită Bolovani de râu cu mortar Zidărie de gabioane Anrocamente Pereuri de pietriş de ¢ 50 mm Stâncă necăptuşită, executată curat Idem cu suprafeţe neregulate colţuroase Canale de pietriş ori de pământ îndesat acoperit cu
0,015 0,017 0,015 0,012 0,014 0,018 0,022 0,027 0,030 0,025 0,022 0,040
66,758,866,783,371,555.745,537,133.340,045,525,0
56

57
Nr crt. Natura pereţilor canalului sau a conductei n ±( 5%) 1/n( %)5±
0 1 2 3
14 15 16 17
20
21
23
u argilă sau pietriş mălit
u maluri înverzite, pe alocuri cu taluzurile
eregulat cu vegetaţie bogată
undiş fix: isip
n=0,030-0,100
ăriş cu iarbă scurtă
a maturitate
ni uţini copaci, iarna
simea medie, iarna vara
frişat cu trunchiuri de copaci fără
n=0,080-0,120 t centrifugat
Fontă curată, nouă
0,027
0,035
0,030
0,040
0,100
0,150
0,060
0,012
37,1
28,6
33,3
25,0
1
10,0
6,7
16.7
83,3
18 19
22
strat fin de argilă sau de nămol fin Idem suprafeţele acoperite cCanale cu prundiş mijlociu Canale de lut cu mici rădăcini ieşite din pământ Canale cstricate Canale cu profil nCanale de drenaj Pâraie şi râuri cu stratul de pr -Pietriş fin cu mult n -Pietriş 10-30 mm -Pietriş 20-60 mm -Pietriş 50-150 mm -Râuri de munte cu bolovani n=0,030-0,035 -Râuri alpine şi carpatine cu albii foarte neregulate Lunci şi câmpii inundabile: -Păşuni şi fâneţe fără tuf -Idem cu iarbă înaltă -Culturi înainte de a da spicul -Culturi ajunse l -Crâng,tufăriş: -Tufăriş risipit, mai mult buruie -Tufăriş cu p -Idem vara -Crâng cu de -Idem -Pădure: -Sălcii crescute des vara -Teren de lăstăriş -Idem cu mult lăstăriş -Arbori în picioare, nivelul inundaţiei sub ramuri Azbociment, cimen
0,017 0,022 0,025
0,030 0,035
0,020 0,022 0,025
0,030 0,035 0,030
0,050 0,050 0,060 0,070
0,040
0,011
58,845,540.0
33,328,6
50,045,540,0
33,328,633,3
20,020,06,79,1
25,0
90,0
b)Formule neexponenţiale.
1. Formula lui H. Bazin (1897) C =
R1
87ρ
+ (4.18)
care ρ = coeficientul de rugozitate; R = raza hidraulică. în

58
Coeficientul de rugozitate r
Tabela 4.2.
crt. N a t u r a p e r e ţ i l o r Nr ρ
1 2 3 1
6
foarte bine
de piatră de talie, beton tencuit simplu,
rămizi puse pe lat
uri, etc.
zitate foarte mare (pietriş, bolovani, stâncă brută, vegetaţie, etc.)
0,06
0,16
1,30
1,75
2 3 4 5
Pereţi foarte netezi (ciment sclivisit, scânduriîncheiate şi şlefuite, căptuşeală cu tablă nouă, etc.) Pereţi netezi(zidăriescânduri brute, etc.) Pereţi puţin netezi (zidărie din moloane sau căşi bine încheiate, zidărie de piatră brută, etc.) Pereţi de pământ bine neteziţi sau acoperiţi cu pereCanale şi râuri regulate cu patul de pietriş mărunt Canale şi râuri cu rugo
0,46 0,85
2. Formula lui I.I.Agroskin C = 17,72(K+logR) (4.19)
ce la modificarea rugozităţii respectiv a vitezei curentului, faţă de prevederile proiectului iniţial.
secţiune transversală a unui curent cu suprafaţă liberă, vitezele medii temporale au diferite v
Curbele de egală viteză se numesc izotahe (fig .4.4).
în care K = parametru funcţie de rugozitatea pereţilor; R = raza hidraulică. Indiferent de formula care se utilizează, alegerea coeficienţilor de rugozitate trebuie
făcută cu mult discernământ, ţinându–se seama de realităţile existente, dar şi de posibilitatea unor modificări posibile în timpul exploatării, care pot du
4.2.3.3. REPARTIŢIA VITEZELOR ÎN SCEŢIUNEA TRANSVERSALĂ. Intr-o alori.
Fig.4.4. Curbele de egală viteză (izotahe)
a medie locală m
vitezelor într-o secţiune transversală a unui curent cu suprafaţă liberă, este redată în figura (4,5).
Se constată că izotahele urmăresc conturul secţiunii aproape paralel, iar vitezaximă nu se află în general la suprafaţa liberă ci puţin mai jos, sub nivelul liber. Epura

Fig.4.5. Epura vitezelor
zVr
= viteza locală medie (temporală) la adâncimea z
59
maxsVr
r= viteza medie maximă de la suprafaţa curentului
maxV = viteza locală medie maximă în profilul curentului
fVr
= viteza medie pe fundul albiei, dată de viteza fictivă ce se obţine din epura vitezelor pe verticală, prin extrapolarea cu tangenta τ , la curba experimentală ABC dusă în punctul cel mai de jos C al curbei, punct în care viteza poate fi măsurată cu aparatele de măsură corespunzătoare.
V = viteza medie pentru întregul profil considerat. In proiectarea lucrărilor de corectarea torenţilor se folosesc următoarele relaţii empirice:
V≅ (0,8….0,9)Vsmax (4.20) V625,0V f ≅ (4.21)
Viteza medie maximă locală Vmax, la canalele obişnuite se află la adâncimea h’ :
h’ = h)41....
201( (4.22)
Această adâncime este cu atât mai mare cu cât pereţii laterali sunt mai apropiaţi şi cu cât rugozitatea albiei este mai accentuată.
4.2.4. DEBITUL. MODULUL DE VITEZĂ ŞI MODULUL DE DEBIT. Debitul într-o secţiune transversală de suprafaţă udată A şi viteză medie V în mişcarea
permanentă şi uniformă este: Q = AV = AC RJ (4.23)
Dacă considerăm J = I = i = 1 obţinem:
-modulul de viteză: MV = C R sau MV = J
V (4.24)
-modulul de debit: MQ =AC R sau MQ = J
Q (4.25)
Aceşti moduli se pot determina şi cu ajutorul nomogramelor (S. A. Munteanu 1963) 4.2.5. PIERDERILE DE SARCINĂ. In cazul mişcării uniforme pierderile de sarcină sunt numai liniare hd = hi, care este
pierdere liniară de sarcină aferentă pantei i. Dar:

=Lhi J = I = i = tgθ≅ sinθ (4.26)
Din formula lui Chézy:
J = RC
V2
2
(4.27)
Insă V = Q/A aşa încât:
J = RCA
Q22
2
(4.28)
Rezultă că:
J = RCA
QRC
VLh
22
2
2
2i == (4.29)
Pierderea liniară de sarcină este:
hi = RCA
LQRC
LV22
2
2
2
= (4.30)
4.2.6. EFORTUL TANGENTIAL LA PERETE. Considerăm acelaşi tronson de albie din figura (4.3) de lungime L, unde condiţia de
echilibru este: T = Gsinθ (4.31)
respectiv τοPL = γALsinθ = γ ALtgθ = γALJ (4.32)
unde το = efortul unitar mediu tangenţial al contactului dintre curent şi peretele albiei
aşa încât: το = 2
2
CVRJJ
PA γγγ == (4.33)
Patratul vitezei medii este:
V2 = γ
τ 2oC
(4.34)
Pierderea de sarcină liniară devine:
hi = RLo
γτ
(4.35)
relaţie ce arată că lucrul mecanic efectuat de forţa de impulsionare este complet consumat de lucrul mecanic al forţelor de frânare.
4.3. STUDIUL ENERGETIC AL CUREN’ILOR CU SUPRAFAŢA LIBERĂ. Studiul energetic al curenţilor cu suprafaţă liberă, începe cu analiza energetică a
mişcărilor uniforme. Aceasta poate fi extinsă, cu erori neglijabile şi la mişcarea gradual variată. La mişcările neuniforme abaterile sunt cu atât mai mari cu cât gradul de neuniformitate
este mai mare. Unele concluzii calitative pot fi extinse în anumite cazuri şi la aceste mişcări. 4.3.1. ENERGII SPECIFICE. Pentru un curent cu suprafaţă liberă, cu mişcare uniformă, energiile specifice într-o
secţiune transversală sunt (fig.4.6) sunt:
60

Fig.4.6. Energiile specifice.
1.Energia specifică a curentului sau energia specifică în lungul curentului sau
sarcina hidrodinamică faţă de planul de comparaţie x’ – x’:
H = z + h + g2
V 2α = z + h + 2
2
gA2Qα (4.36)
2.Energia specifică a secţiunii sau energia specifică a suprafeţei udate A sau sarcina hidrodinamică faţă de planul de comparaţie x – x:
HA = h + g2
V 2α = h + 2
2
gA2Qα (4.37)
4.3.2. MIŞCĂRI LENTE ŞI MIŞCĂRI RAPIDE. Într-o secţiune dată, la un debit Q constant, într-o mişcare permanentă, energia
specifică a secţiunii HA este funcţie numai de h: HA = f(h) ; [ A = f1(h)] (4.38)
Din relaţia (4.38):
-pentru h→0 avem: 2
2
gA2Qα → +∞ ( A ) deci HA (4.39) 0→ +∞→
-pentru h avem: +∞→ 2
2
gA2Qα 0→ (A ∞→ ) deci (4.40) +∞→AH
Reprezentarea grafică a variaţiei energiei specifice a secţiunii HA ,funcţie de adâncimea h, pentru un debit Q = constant, este redată în figura (4.7).
61

Fig.4.7. Variaţia energiei specifice a secţiunii. Din analiza variaţiei energiei specifice a secţiunii rezultă: -Curba are un minim în punctul ce coordonate C(hcr,HAminim), ceea ce arată că mişcarea
nu este posibilă decât dacă HA > HAminim. -Pentru o energie specifică a secţiunii dată HA > HAminim, corespund două stări de
mişcare (curgere) calitativ diferite: I- Stare (regim) lent de curgere, denumit şi regim fluvial sau subcritic de curgere, cu
adâncimea hI cu punctul I pe ramura superioară a curbei, pentru care:
dhdH A > 0 iar hI > hcr (4.41)
unde hcr este adâncimea critică, iar funcţia este crescătoare pe ramura C – I. II- Stare (regim) rapid de curgere, denumit şi regim torenţial sau supracritic de
curgere, cu adâncimea hII cu punctual II pe ramura inferioară a curbei, pentru care:
dhdH A < 0 iar hII< hcr (4.42)
funcţia fiind descrecătoare pe ramura C – II. Adâncimile hI şi hII se numesc adâncimi alternante. Pentru cazul când:
HA = HAminim : 0dh
dH A = : h = hcr (4.43)
starea sau regimul de curgere se numeşte stare critică sau regim critic căruia îi corepunde adâncimea critică hcr.
Pentru un anumit debit Q corespunde numai singură adâncime critică şi un singur HAminim.
Derivând relaţia:
HA = h + 2
2
gA2Qα unde A = A(h) (4.44)
în raport cu h obţinem:
dhdA
gAQ1
dhdH
3
2A α
−= (4.45)
62

Interpretarea derivatei dhdA rezultă din figura (4.8) unde:
dA = Bdh iar BdhdA
= (4.46)
Fig.4.8. Interpretarea derivatei dA/dh.
B este lăţimea la oglinda apei. Relaţia (4.45) devine:
3
2A
AB.
gQ1
dhdH α
−= (4.47)
Relaţiile (4.41), (4.42) şi (4.43) constituie criteriul derivatei de recunoaştere a regimului de mişcare.
4.3.3. ALTE CRITERII DE RECUNOAŞTERE A REGIMULUI DE MIŞCARE. 4.3.3.1. CRITERIUL FROUDE. In locul criteriului derivatei, se introduce un alt criteriu reprezentat de termenul
adimensional denumit numărul lui Froude notat cu Fr :
Fr = ===m
c
m
2
3
2
hH2
ghV
AB.
gQ αα V
mghα ; Pentru α = 1
mghVFr =→ (4.48)
unde s-a înlocuit Q/A =V şi B/A = hm adâncimea medie a curentului. Din relaţia (4.48) rezultă că mumărul Froude este proporţional cu raportul dintre
dublul energiei cinetice Hc şi energia potenţială a curentului hm. Relaţia (4.47) devine:
Fr1dh
dH A −= (4.49)
Pentru: Fr < 1 mişcarea este în regim lent Fr = 0 mişcarea este în regim critic Fr > 1 mişcarea este în regim rapid.
4.3.3.2. CRITERIUL ADÂNCIMII. ADÂNCIMEA CRITICĂ. Aplicarea criteriului adâncimii implică cunoaşterea adâncimii critice hcr. Punând
condiţia de minim relaţiei (4.47) căreia îi corespund B = Bcr şi A = Acr, corespunzătoare adâncimii critice hcr avem:
0AB
.gQ1
dhdH
3cr
cr2
A =−=α (4.50)
de unde:
f(hcr) = cr
3cr
2
BA
gQ
=α (4.51)
63relaţie care reprezintă expresia generală a curgerii în regim critic.

Se observă că această relaţie nu depinde nici de pantă şi nici de rugozitate. Calculul adâncimii critice. Debitul fiind constant, adâncimea critică satisface ecuaţia generală (4.51) scrisă sub
forma:
crmcrcrcr
crcr hA
BA
Ag
Q φ
α
=== (4.52)
unde hmcr = adâncimea hidraulică medie critică; crφ = factorul secţiunii pentru calculul adâncimii critice.
1. metoda grafo-analitică.
-Cu ajutorul relaţiei BAhA)h(
3
m ==φ (4.53)
se construieşte curba φ (h) figura (4.9).
Fig.4.9. Graficul curbei φ (h).
-Pentru un debit constant Q se calculează factorul corespunzător crφ cu relaţia:
α
φg
Qcr = (4.54)
-Ordonata Oh corespunzătozre punctului M de pe curba φ (h) aferentă abscisei obţinute din relaţia (4.54), reprezintă grafic mărimea adâncimii critice hcr care stisface ecuaţia (4.52).
2. Metoda prin încercări succesive. In relaţia mhA)h( =φ se dau valori din aproape în aproape , până cănd se ajunge la
valoare factorului crφ calculată cu relaţia (4.54). Pentru: h > hcr mişcarea este lentă
h = hcr mişcarea este în regim critic. h < hcr mişcarea este rapidă
4.3.3.3. CRITERIUL VITEZEI. VITEZA CRITICĂ. Corespunzător unei adâncimi critice avem ţi o viteză critică a curentului Vcr:
0Vgh
1dh
dH 2cr
mcr
A =−=α (4.55)
de unde:
64

Vcr = cr
mcr
AQgh
=α
(4.56)
Deoarece:
Q = Acrα
mcrgh (4.57)
Pentru α = 1 Vcr = 3,132 mcrh (4.58)
Viteza critică, rezultă şi din criteriul Froude pentru Fr = 1:
Fr = α
α mcr
mcr
2cr gh
V1gh
V=→= (4.59)
Pentru: V < Vcr mişcarea este lentă V = Vcr mişcarea este în regim critic V > Vcr mişcarea este rapidă
La un curent deosebim două stări critice. Prima stare critică este trecerea de la mişcare laminară la mişcare turbulentă, iar viteza critică defineşte a doua stare critică.
4.3.3.4. CRITERIUL PANTEI. PANTA CRITICĂ. Criteriul pantei este aplicabil numai în cazul mişcărilor permanente uniforme, deoarece
la o secţiune de formă dată şi un debit dat, mişcarea uniformă este complet determinată de pantă. Pentru mişcări neuniforme gradual variate, pentru determinarea mişcării trebuie să se cunoască şi o cotă de comandă.
In mişcarea permanentă uniformă adâncimea curentului h se numeşte adâncime normată.
S-a arătat că adâncimea critică nu depinde de panta albiei, aşa încât la o anumită valoare a pantei, adâncimea normată este egală cu adâncimea critică, caz în care panta este panta critică:
h = hcr i = icr (4.60) →Dar
Q = AC Ri şi BA
gQ 32
=α (4.61)
aşa încât
cr2cr
cr
cr2cr
mcr
crcr2cr
crcr BC
gPRC
ghBRC
gAi
ααα=== (4.62)
Pentru albii foarte largi hR ≅ şi BP ≅ aşa încât:
Cgiα
≅ (4.63)
Fig.4.10. Graficul funcţiei i = f(h).
65

Din reprezentarea grafică a funcţiei i = f(h) figura (4.10), rezultă că la un debit Q dat, pentru: ireal < icr mişcarea este în regim lent
ireal = icr mişcarea este în regim critic ireal > icr mişcarea este în regim raid.
4.4. MIŞCAREA PERMANENTĂ GRADUAL VARIATĂ. 4.4.1. GENERALITĂŢI. Mişcarea permanentă uniformă este un caz particular al mişcării permanente, localizat
în canale şi anumite sectoare de albii regularizate, unde secţiunea transversală, panta longitudinală şi rugozitatea sunt constante.
Albiile naturale şi canalele de pământ în timp îşi modifică caracteristicile hidraulice, şi cu atât mai mult datorită unor lucrări transversale şi longitudinale amplasate pe parcurs.
Dacă debitul este constant şi parametrii secţiunilor transversale variază lent de la o secţiune la alta, mişcarea curentului este o mişcare permanentă gradual variată sau o mişcare neuniformă gradual variată.
In figura (4.11) sunt redate câteva forme care determină mişcarea variată în albiile deschise.
Fig.4.11. Forme ale albiilor deschise.
4.4.2. SECŢIUNEA DE COMANDA. Studiul mişcării gradual variate se reduce la determinarea relaţiilor între adâncimea h a
curentului dintr-o secţiune dată şi distanţa L măsurată până la o secţiune de referinţă denumită secţiune de comandă sau secţiune de control.
Secţiunea de comandă (control) este caracterizată de faptul că impune o cotă determinată suprafeţei libere, care în general depinde de debit.
Cota secţiunii de control se numeşte cota de comandă sau cota de control pentru suprafaţa liberă care se formează.
Relaţiile ce se stabilesc trebuie să ducă în final la posibilitatea trasării curbei suprafeţei libere a curentului.
66

4.4.3. ECUAŢIA GENERALĂ DIFERENŢIALĂ A MIŞCĂRII PERMANENTE GRADUAL VARIATE.
Considerăm un tronson de albie deschisă (fig.4.12) cu ≤θ 6o, o secţiune de control 0-0,
o secţiune oarecare 1-1 la distanţa L de secţiunea de control şi o secţiune 2-2 la distanţa elementară dL.
Fig.4.12. Tronsonul de albie deschisă.
Se admite ipoteza că liniile de curent sunt rectilinii şi paralele, care de fapt în realitate sunt curbe.
In acest caz ecuaţia lui Bernoulli are forma:
idL + h1 + =g2V 2
11α h2 + g2V 2
22α + dhr (4.64)
Însă h = f(L) ; A = f(h,L) ; Q = constant ; hr1-2 = hd = JL ; dA = Bdh ; dA/dh = B = / iar A∂ h∂ ααα == 21 datorită curburei reduse a liniilor de curent.
h2 – h1 = dh = idL -g2
)VV( 21
22 −α - dhr (4.65)
sau: dh = idL - g2
)V(d 2α - dhr (4.66)
Dar V2 = 23
22
2
QAdA2)V(d
AQ
−=⇒ ; dA = dLLABdhdL
LAdh
hA
∂∂
+=∂∂
+∂∂
aşa încât relaţia (4.66) devine:
dh = idL + r3
2
dh)dLLABdh(
gAQ
−∂∂
+α (4.67)
Împărţind relaţia (4.67) cu dL obţinem:
dLdh
LA.
gAQ
dLdh.
gABQi
dLdh r
3
2
3
2
−∂∂
++=αα (4.68)
Dar dhr/dL = J panta hidraulică, deci:
JLA.
gAQi)
gABQ1(
dLdh
3
2
3
2
−∂∂
+=−αα (4.69)
Insă Q = ACRCA
QJRJ 22
2
=⇒ iar FrgA
BQ3
2
=α numărul lui Froude aşa încât:
67

Fr1
)LA
gARC1(
RCAQi
dLdh
2
22
2
−∂∂
−−=
α
(4.70)
este ecuaţia generală diferenţială a curbei suprafeţei libere în mişcarea neuniformă gradual variată în albii neprismatice cu neunuformitate spaţială redusă.
-Pentru albii prismatice cu secţiune constantă si mişcare pemanentă neuniformă gradual variată:
Fr1Ji
Fr1RCA
Qi
dLdh0
LA 22
2
−−
=−
−=⇒=
∂∂ (4.71)
-Pentru albii prismatice cu mişcare permanentă uniformă, secţiunea udată nu variază nici funcţie de h şi nici funcţie de L deci:
0RCA
Qi0dLdh
22
2
=−⇒= sau i – J = 0 şi i = J = RC
VRCA
Q2
2
22
2
=
care reprezintă relaţia lui Chézy pentru mişcarea permanentă uniformă: V = C RJCRi = (4.72)
4.4.4. FORMA ŞI CALCULUL CURBELOR SUPRAFEŢELOR LIBERE. 4.4.4.1. FORMA CURBELOR SUPRAFEŢELOR LIBERE. Forma curbelor suprafeţelor libere sunt forma liniilor piezometrice ale curenţilor în
mişcarea gradual variată, date de ecuaţiile diferenţiale de la (4.4.3). Formele acestor curbe se numesc remuu sau curbe de remuu. Formele de remuu sunt: -Remuul pozitiv, când nivelul apei se umflă datorită stăvilirii curgerii prin baraje, caz în
care curba are comcavitatea în sus (fig.4.11.d). -Remuul negativ, când nivelul apei scade datorită ruperii pantei în spre aval ca de
exemplu: trecerea peste un prag (fig.4.11.e), peste un deversor, canal în trepte, etc. La remuul negativ nivelul apei scade după o formă conexă în sus.
4.4.4.2. CACULUL CURBELOR SUPRAFEŢELOR LIBERE:
4.4.4.2.1.Calculul cotelor suprafeţelor libere în albii primatice. In cazul albiilor prismatice, calculul se efectuiază prin integrarea ecuaţiei diferenţiale
(4.71) pentru diverse forme de secţiuni 4.4.4.2.2.Calculul cotelor suprafeţelor
libere în albii prismatice
Fig.4.13. Curba de stăvilire.
1.Metoda prin integrarea ecuaţiei diferenţiale (4.70).
Se porneşte de la o secţiune de control, care în cazul figurii (4.13) este secţiunea 0 –0 poziţionată în dreptul barajului unde nivelul apei este cunoscut (nivel care corespunde debitului maxim de verificare) Prin integrare din aproape în aproape, se obţin în mod succesiv adâncimile h1, h2,…hk …corespunzătoare distanţelor L1, L2,…Lk…. Prin unirea punctelor de coordonate (Lk,hk), se obţine curba suprafeţei libere a curentului în amonte de baraj, curbă care se numeşte curba de stăvilire.
2.Metoda albiei fictive.
68
Această metodă presupune înlocuirea albiei naturale cu o albie prismatică echivalentă, la are se

aplică metodele expuse. Metoda este aplicabilă, fără erori prea mari sectoarelor cu albii relativ uniforme, apropiate de albiile prismatice, ceea ce implică sectoare scurte.
3.Metoda diferenţelor finite pe tronsoane (Metoda Standard). Constă în împărţirea albiei în sectoare, delimitate prin secţiuni de calcul, între care se
aplică relaţia lui Bernoulli sub forma ee finită. Această metodă este frecvent folosită, deşi volumul de calcule numerice este mare,dar
aceste calcule efectuându-se cu uşurinţă cu ajutorul calculatoare.lor.. La stabilirea sectoarelor trebuie avute în vedere următoarele reguli generale (fig.4.14):
Fig.4.14. Stabilirea sectoarelor de calcul în metoda standard.
-Se apreciază lungimea totală a albiei pe care este modificată curba suprafeţei libere,
care urmează a fi calculată; -Se împarte albia în sectoare da calcul, care să cuprindă porţiuni cu caracteristici de
albie apropiate ca formă, adâncime, secţiune, astfel încât să fie cât mai uniforme; -Lungimile sectoarelor de calcul să nu difere prea mult; -Secţiunile de calcul care delimitează sectoarele să coincidă dacă este posibil cu secţiuni
în care s-au efectuat măsurători (nivele, debite); -Lungimile sectoarelor de calcul să fie astfel amplasate încât diferenţa de nivel între
extremităţile lor să nu varieze mai mult de 5 – 10 centimetri. Odată stabilită secţiunea de comandă (control) şi a fost determinată cota de
comandă(control), calculul se face astfel: -spre amonte dacă mişcarea este lentă (fig.4.14.a); -spre aval dacă mişcarea este rapidă (fig.4.14.b)- Mai întâi se calculează cota suprafeţei libere în secţiunea 1-1, având ca sprijin secţiunea
de control 0-0. Apoi se calculează cota din secţiunea 2-2, având ca secţiune de sprijin secţiunea 1-1, a cărei cotă a fost determinată la pasul anterior 0-1. Operaţiunea se repetă până la secţiunea finală.
Un pas de calcul de la secţiunea k la secţiunea k+1 se rezolvă cu ecuaţia lui Bernoulli:
rkk
2
k1k
2
1k h)g2
V(H)g2
V(H ++=+ ++αα (4.73)
Hk = zk + hk este cota suprafeţei libere, egală cu cota piezometrică în secţiune; hrk este pierderea de sarcină pe sectorul (k+1) – k. Inlocuind în relaţia (4.73) viteza V = Q/A obţinem:
rk21k
2k
2
k1k h)A
1A1(
g2QHH +−+=
++
α (4.74)
Ecuaţia este implicită în Hk+1, deoarece în partea dreaptă Ak+1 şi hrk sunt funcţii de Hk+1.
Ecuaţia se rezolvă astfel: 69

-se alege pentru Hk+1 o valoare ; )o(1kH +
-se calculează pentru aceasta, valorile lui Ak+1, care se introduce în partea dreaptă a ecuaţiei (4.74) şi se obţine o nouă valoare notată cu . )1(
1kH +
Dacă: (4.75) ε≤− ++ ]HH[ )0(1h
)1(1k
în care ε este eroarea admisă ( 100/zkΔε ≈ ) atunci valoare Hk+1 este corectă, se poate trece la calculul lui Hk+2..
Dacă condiţia (4.75) nu este satisfăcută, trebuie aleasă şi încercată o nouă valoare (aproximaţie) pentru , până se ajunge să fie satisfăcută această condiţie. Este de dorit ca: )1(
1kH +)0(1k
)1(1k HH ++ = (4.76)
4.4.5. SALTUL HIDRAULIC. 4.4.5.1. DEFINIŢIA SALTULUI HIDRAULIC. FORME. Saltul hidraulic este o formă caracteristică de mişcare cu suprafaţă liberă, prin care se
trece de la mişcarea în stare rapidă la mişcarea în stare lentă. In saltul hidraulic, mişcarea are o neuniformitate pronunţată, cu o creştere relativ bruscă
a adâncimilor şi o modificare importantă a distribuţiei vitezelor. Saltul hidraulic are forme variate. O sistematizare a acestor forme a fost făcută de
Bradley şi Peterka, clasificându-le după numărul lui Froude la intrare. In figura (4.15) sunt redate cinci forme.
Fig.4.15. Forme ale saltului hidraulic.
Când saltul hidraulic este prea înalt el se răstoarnă în sens invers curgerii şi formează o
saltea rostogolitoare, care de multe ori se deplasează spre amonte.
70

4.4.5.2. ELEMENTELE SALTULUI HIDRAULIC. Principalele elemente ale saltului hidraulic sunt (fig.4.16):
Fig.4.16. Elementele saltului hidraulic.
-h1 adâncimea de intrare în salt; -h2 adâncimea de ieşire din salt; -hcr adâncimea critică; -h2-h1 înălţimea saltului; -Ls lungimea saltului.
Locul saltului se găseşte la intersecţia celor două linii energetice, de exemplu cea amonte corespunde regimului rapid cu cea din aval corespunzând regimului lent.
Lungimea saltului se calculează după diverse formule. De exemplu: -Bradley şi Peterka: Ls = 6,15 h2 pentru 20 < Fr <120 (4.77) -Certusov: Ls = 10,3 h1( Fr - 1) (4.78) 81,0
Ad\ncimile de intrare şi de iesire sunt:
h1 = 0,5h2( )1)hh
(81 3
2
cr −+ ; h2 = 0,5h1( )1)hh
(81 3
1
cr −+ (4.79)
Cunoscând una din adâncimi se poate determina cealaltă. Adâncimile h1 şi h2 sunt adâncimi conjugate (alternante). La definirea lungimii saltului hidraulic există unele dificultăţi datorită faptului că
intervin elemente subiective la stabilirea secţiunii de ieşire din salt . 4.4.6. SCURGEREA TORENŢIALĂ. 4.4.6.1. CONSIDERAŢIUNI GENERALE . Scurgerea torenţială denumită în mod curent şi viitură tor4enţială este feomenul
priencipal al procesului torenţial- Acest fenomen se datorează ploilor torenţiale şi a topirii bruşte a zăpezilor, Fără scurgere torenţială nu pot avea loc celelalte trei feomene torenţiale: eroziunea torenţială, transportul torenţial şi sedimentarea torenţială.
Studiul ploilor torenţiale şi al fenomenelor torenţiale, constituie obiectul hidrologiei bazinelor hidrografice torenţiale.
Studiul procesului torenţial şi al fenomenelor torenţiale nu este posibil fără cunoaşterea temeinică a hidraulicii scurgerii torenţiale.
4.4.6.2. CARACTERISTICILE HIDRAULICE ALE SCURGERII TORENŢIALE. Scurgerea torenţială este constituită din mişcarea fluidului format din apă şi aluviunile
rezultate din fenomenul de erodare. Hidraulic, scurgerea torenţială este o mişcare: - cu suprafaţa liberă, după conturul tubului de curent - nepermantă, după criteriul variaţiei în timp a presiunii şi vitezei - neuniformă, după modul de desfăşurare a liniilor de curent - în regim rapid (torenţial), după criteriul Froude Fr>1 - eterogenă, după criteriul mişcării vitezei relative - turbulentă. după regimul de mişcare al lichidului purtător - pulsatorie, datorită caracterului turbulent al mişcării - cu un debit cu creşteri bruşte, (maximul chiar în câteva zeci de secunde). - cu un flux de energie cinetică foarte mare.
71

5. HIDRAULICA CONSTRUCŢIILOR PENTRU CORECTAREA TORENŢILOR. 5.1. GENERALITĂŢI. Corectarea torenţilor implică o serie de construcţii hidrotehnice specifice grupate în
două mari categorii şi anume: lucrări transversale şi lucrări longitudinale, care se execută pe reţeaua hidrografică şi versanţii bazinelor hidrografice torenţiale, ca parte a complexului de lucrări necesare amenajării acestor bazine.
Diversitatea formelor pe care le prezintă aceste construcţii, generează tot atâtea tipuri de probleme de hidraulică.
In acest context, se remarcă hidraulica: deversoarelor, radierelor, confuzoarelor, canalelor, evazoarelor, (fig.5.1).
Fig.5.1. Deversor, radier, confuzor, canal, evazor.
Specificul construcţiilor hidrotehnice pentru corectarea torenţilor se poate concretiza
prin următoarele câteva caracteristici esenţiale: -au un grad mare de neuniformitate, cu o mare varietate de forme specifice; -amplasamentul construcţiilor se află în zone cu accesibilitate redusă şi relief dificil; -există o strânsă legătură între latura funcţională şi cea a siguranţei construcţiilor; -adoptarea lor, necesită în prealabil, efectuarea unor studii şi analize foarte complexe
(tehnice, ecologice, economice, sociale, orgsnizatorice, etc.) care să conducă la elaborarea şi adoptarea unor soluţii optime din toate punctele de vedere.
72

5.2. ORIFICII. AJUTAJE. BARBACANE. 5.2.1. DEFINTII. CLASIFICĂRI. 5.2.1.1. DEFINIŢII. Orificiul este o deschidere în peretele unui rezervor, prin care lichidul curge sub
presiune, astfel încât curentul efluent denumit –vână lichidă- sau –jet-, să fie în contact numai cu muchia interioară a deschiderii. Înseamnă că lichidul efluent udă întotdeauna întregul contur al muchiei interioare a orificiului (fig.5.2).
Ajutajul este o conductă scurtă cu forme speciale, ataşată etanş unui orificiu, destinată să formeze o vână de lichid, să dirijeze această vână sau să-i modifice proprietăţile hidraulice.
Barbacanele sunt deschideri de diferite forme şi dimensiuni, practicate în corpul barajelor de corectarea torenţilor, care au ca scop evacuarea apei acumulate în bieful amonte. Barbacanele se asimilează din punct de vedere hidraulic cu ajutaje.
Fig.5.2. Orificii şi ajutaje.
5.2.1.2. CLASIFICAREA ORIFICIILOR (fig.5.2). a)După grosimea pereţilor avem:
-Orificii cu pereţi subţiri……………………………2ae ≤
-Orificii cu pereţi groşi (ajutaje)………………….. e<2a
b)După mărime: -Orificii mici ………………..a≤0,5H sau d≤0,5H -Orificii mari………………..a>0,5H sau d>0,5H
73

La orificiile mici se poate considera că sarcina H este constantă în orice punct al orificiului, ceea ce permite să se admită în calculul debitelor o distribuţie uniformă a vitezelor în secţiunea contractată a jetului.
La orificiile mari distribuţia vitezelor în plan vertical nu este uniformă în secţiune, calculul debitelor fiind diferit faţă de orificiile mici.
c)După regimul de mişcare: -Orificii în regim permanent, când sarcina H şi debitul sunt constante. -Orificii în regim nepermanent, când H şi debitul variază în timp.
d)După poziţia în spaţiu: -Orificiile pot fi verticale, oblice sau orizontale.
e)După nivelul apei din aval: -Orificiile pot fi libere, semiînecate sau înecate.
5.2.2. SECTIUNEA CONTRACTATĂ. Particulele de lichid se deplasează spre orificiu după traiectorii convergente. Această
convergenţă se accentuiază cu cât particulele sunt mai apropiate de orificiu şi de pereţii săi directori.
După atingerea muchiei de intrare, fenomenul de convergenţă se manifestă şi în aval pe o anumită porţiune în lungul venei şi se accentuiază în virtutea inerţiei şi direcţiei pe care sunt angajate particulele în mişcare. Aceasta are ca efect o reducere, respectiv o contracţie treptată a secţiunii vânei până la o valoare minimă în raport cu aria orificiului Ac
Secţiunea de arie minimă Ac se numeşte secţiune contractată. In secţiunea contractată mişcarea este gradual variată, astfel încât firele de lichid pot fi
considerate paralele, vitezele aproximativ egale şi paralele, iar distribuţia presiunilor sensibil apropiată de cea din mişcarea uniformă. In consecinţă sarcina orificiului H se poate măsura în cazul orificiilor libere, până la centrul orificiului (fig.5.2.).
Raportul ε dintre aria secţiunii contractate Ac a vânei de lichid şi aria secţiunii orificiului A se numeşte coeficient de contracţie:
AA
AA c
or
c ==ε <1 (5.1)
Coeficientul de contracţie este subunitar şi depinde de felul construcţiei, sarcina în orificiu, înălţimea acestuia, natura şi vâscozitatea lichidului.
Coeficientul de contracţie se poate determina teoretic cu ajutorul teoremei impulsului, cât şi experimental, valorile corespund între ele.
5.2.3. ORIFICII MICI ÎN REGIM PERMANENT. 5.3.2.1. VITEZA. Consider[m un orificiu mic liber vertical în regim permanent (fig.5.2) în care:
H -sarcina orificiului V0 -viteza de acces în rezervor, suficient de departe de orificiu
H0 = H + g2V 2
00α -sarcina totală a orificiului (5.2)
p0 -presiunea la nivelul liber al orificiului p -presiunea la nivelul secţiunii contractate Ac α0 , α –coeficienţii lui Coriolis în secţiunile 0-0 şi C-C
Aplicând ecuaţia lui Bernoulli pentru secţiunea de la nivelul liber 0-0 şi secţiunea contractată C-C:
74

z1 + g2Vpz
g2Vp 22
000 αγ
αγ
++=+ + hr0-C (5.3)
Insă p0 = p = pa presiunea atmosferică, iar α0 = α = 1 deoarece în secţiunile de calcul distribuţia vitezelor este uniformă.
Pierderea de sarcină locală între cele două secţiuni de calcul este:
hr0-C = g2
V 2
ξ (5.4)
unde ξ este coeficientul rezistenţelor locale sau coeficientul de pierdere de sarcină locală la trecerea jetului prin orificiu.
Ecuaţia lui Bernoulli devine:
z1 – z + g2
Vg2
Vg2
Vpp 2220aa ξ
γγ+=+− (5.5)
sau: H + )1(g2
Vg2
V 220 ξ+= (5.6)
de unde: V = t0
20 VgH2)g2
VH(g2
11 ϕϕξ
==++
(5.7)
unde: V este viteza reală a jetului în secţiunea contractată Vt = 0gH2 este viteza teoretică a jetului ce trece prin orificiu
ξϕ
+=
11 este coeficientul de viteză, care corectează viteza teoretică Vt pentru a obţine
viteza reală V.
Dacă factorul cinetic calculat cu V0 este foarte mic faţă de H adică g2
V 20 < H pentru că
H H0 expresia vitezei reale V are forma uzuală: ≈gH2V ϕ= (5.8)
având evident: H
H P=ϕ şi H – HP =Hξ
ξ+1
= hr0-C (5.9)
Aceasta rezultă dacă introducem în jet un tub Pitot, observăm că lichidul se ridică la înălţimea HP (fig.5.2).Rezultă că:
V2 = φ2.2gH = 2gHP de unde H/H P=ϕ iar H-HP=H-φ2H=H(1-φ2)=Hξ
ξ+1
Pentru apă Weissbach a găsit valoarea medie de φ = 0,97 pentru care rezultă 064,0≈ξ şi H - HP 06.0≈
5.2.3.2. DEBITUL VOLUMIC. Debitul volumic evacuat de un orificiu mic liber dintr-un perete vertical este:
Q = AcV = εAV = εφA 0gH2 = μΑ 0gH2 (5.10) care este formula generală a debitului, iar
μ = εφ (5.11) este coeficientul de debit al orificiului.
Pentru: g2V 2
00α < H debitul este Q = μA gH2 (5.12)
Valorile coeficienţilor ε, φ, μ, variază în funcţie de forma şi dimensiunile orificiului, sarcina H, natura şi vâscozitatea lichidului, viteza de acces.
75

Pentru orificii mici circulare în pereţi verticali, cu contracţie perfectă se pot folosi următoarele valori:
ε = 0,96....0,64 valorile mici fiind valabile pentru sarcini mari şi invers. φ = 0,96....0,99 μ = 0,59.....0,63 se ia în medie μ = 0.60 iar la sarcini foarte mici μ ajunge la
la valoarea 0,70. Pentru aceşti coeficienţi sunt întocmite tabele cu valori obţinute experimental. 5.2.3.3. DETERMINAREA TEORETICĂ A COEFICIENTULUI DE CONTRACŢIE. Determinarea teoretică a coeficientului de contracţie se efectuiază cu ajutorul teoremei
impulsului (fig.5.2):
HAVdtdm
t γ= = P (5.13)
unde P este forţa hidrostatică de impuls la gura orificiului, unde diagrama presiunilor este un trapez cu latura mică p1= γ(H – a/2) şi cu latura mare p2= γ(h + a/2), presiune ce se exercită pe lungimea b, deci :
P = HAab)pp(21
21 γγ =+
Masa de lichid pe secundă este:
tAVg
Qgdt
dm εγγ== (5.14)
iar =tVdtdm HAAV
g2
t γεγ = (5.15)
Dar gH2Vt = de unde g2
VH
2t=
aşa încât relaţia (5.15) devine:
AVg2
AVg
2t
2t
γεγ =
de unde: 21
=ε = 0,5 (5.16)
Dacă în loc de viteza teoretică Vt, folosim viteza reală gH2V ϕ= obţinem:
221ϕ
ε = (5.17)
iar ε
ϕ21
= şi μ = ϕεε=
2 (5.18)
5.2.4. ΟRIFICII MARI ÎN REGIM PERMANENT. 5.2.4.1. ORIFICII MARI LIBERI. La orificiile mari verticale, vitezele în diferite puncte ale secţiunii contractate variază
sensibil, în funcţie de sarcina z (fig.5.3). Debitul elementar într-o secţiune elementară orizontală este:
76

Fig.5.3. Orificiu mare liber.
gz2dAdQ μ= (5.19)
unde: dA = bdz ; b = f(z) deci dA = f(z) deci:
dzzb.g2dQ μ= (5.20)
aşa încât: dzzbg2Q 2
1
H
H∫= μ (5.21)
Pentru integrarea relaţiei (5.21) care este formula generală a debitului trebuie cunoscută forma geometrică a orificiului, deoarece b = f(z).
Coeficientul de debit μ este şi el variabil cu înălţimea z, care însă este considerat constant, ca fiind valoarea medie pentru toate firele de lichid din jet.
În mod curent se foloseşte formula de la debitul orificiilor mici (5.12), dacă se ia în calcul o sarcină medie Hm convenabil aleasă, obţinându-se astfel formula simplificată a debitului.
-Debitul orificiului dreptunghiular de dimensiune a şi b=const. este:
77
== ∫ dzzg2bQ2
1
H
H
2/1μ =2H
H
23
z32g2bμ ⎟⎟
⎠
⎞⎜⎜⎝
⎛− 2
3
123
2 HHg2b32 μ (5.22)
⎥⎥⎥
⎦
⎤
⎢⎢⎢
⎣
⎡
⎟⎟⎠
⎞⎜⎜⎝
⎛+−⎟⎟
⎠
⎞⎜⎜⎝
⎛+=
23
2o
1
23
20
2 g2V
Hg2
VHg2b
32Q μsau: (5.23)
Pentru determinarea formulei simplificate, considerăm debitul:
m
H
H
gH2Adzzbg2Q2
1
μμ == ∫ (5.24)
unde A = b(H2 – H1). Prin echivalenţă avem:
( ) m1223
123
2 gH2HHbHHg2b32
−=⎟⎟⎠
⎞⎜⎜⎝
⎛− μμ (5.25)
de unde: 12
23
123
2m HH
HH.32H
−−
= (5.26)
Practic sarcina medie Hm se consideră ca sarcină medie din centrul de greutate al orificiului, adică sarcina H multiplicată cu un coeficient de corecţie 1≤δ , aşa încât:

2
HHHH 21m
+== δδ (5.27)
Se constată că la orificiile dreptunghiulare, dacă se înlocuieşte Hm cu H. deci δ =1, comite o eroare prin exces foarte mică, pentru cazurile curente aceasta este sub 4%, eroare de acelaşi ordin de mărime şi la orificii de alte forme. Formulele simplificate sunt: ( ) gH2AgH2HHbQ 12 μμ =−= ; Q = ( ) 0012 gH2AgH2HHb μμ =− (5.28)
-Debitul orificiului circular. Pentru o secţiune circulară: 22 )zH(r2b −−= (5.29) Formula generală a debitului este:
( )[ ]{∫+
−
−−=rH
rH
22 zHrzg22Q μ } (5.30)
Formula simplificată este: 0
22 gH2rQ;gH2rQ μπμπ == (5.31) -Alte orificii. Formula simplificată pentru orificii cu alte secţiuni este: 0gH2AsauQgH2AQ μμ == (5.32)
unde: H0 = H + g2
V 20 pentru α=α0=1
5.2.4.2. ORIFICII CU MUCHII ASCUŢITE ÎNECATE ÎN AVAL. Se disting două două tipuri: orificii semiînecate (fig.5.4.a) şi orificii înecate (fig.5.4.b).
Fig.5.4. Orificii înecate în aval.
-Debitul pentru orificiile dreptunghiulare semiînecate este:
( )⎥⎥⎦
⎤
⎢⎢⎣
⎡−+⎟⎟
⎠
⎞⎜⎜⎝
⎛−= a12
23
123
a gH2HHHH32g2bQ μ (5.33)
-Debitul pentru orificii dreptunghiulare înecate este:
a12 gH2)HH(bQ −= μ (5.34) Formula simplificată a debitului pentru orificiile înecate este:
agH2AQ μ= (5.35) 78

5.2.5. ORIFICII CU AJUTAJE. În practică orificiile cu muchii ascuţite, se folosesc doar în laboratoare, uzine
hidroelectrice, staţii de pompare, etc., în scopul măsurării debitelor. Pentru nevoile de simplă evacuare a apelor, sau de golire a rezervoarelor se folosesc
ajutajele. Muchiile de intrare pot fi: ascuţite(vii), teşite, sau rotunjite, coeficientul de debit μ
crescând. 1. Ajutaje tubulare (fig.5.5), care au diametrul (dimensiunile transversale)constant. Pentru ajutajele de lungime l = (3…5)d coeficienţii de debit sunt (Dorin Pavel):
Fig.5.5 Ajutaje tubulare.
-muchii ascuţite (vii) la 900 (fig.5.5.a)……………μ = 0,82 -muchii slab teşite (fig.5.5b)..................................μ = 0,90 -muchii rotunjite bine (fig.5.5.c)…………………μ = 0,97
2. Αjutaje convergente (fig.5.6.a) şi divergente (fig.5.6.b) la care coeficienţii de debit sunt funcţie de unghiul α şi raportul l/d.
Fig.5.6 Ajutaje convergente şi divergente. Pentru aceste ajutaje cât şi pentru ajutaje de alte forme sunt întocmite tabele cu coeficienţii de
debit. 5.2.6.BARBACANE ÎN REGIM PERMANENT. Barbacanele sunt ajutaje tubulare sau conducte scurte de golire, din elevaţia barajelor,
pentru evacuarea unei părţi a apei acumulate în bieful amonte, în timpul viiturilor torenţiale. Secţiunea barbacanelor poate fi circulară, dreptunghiulară sau patrată.
79

Fig.5.7. Barbacană liberă şi înecată.
Formulele simplificate pentru calculul debitelor sunt pentru:
80
- barbacane libere (neînecate) Q = gH2Aμ (5.36)
- barbacane inecate Q = agH2Aμ (5.37) Spre deosebire de orificii, coeficientul de debit
este exprimat prin pierderile liniare de sarcină, datorită faptului că vâna de lichid rămâne lipită de pereţii barbacanei, şi chiar dacă pe o lungime scurtă există o contracţie, această vână îşi recapătă forma iniţială, umplând spre ieşire întreaga secţiune, deci:
ϕεϕμε ==⇒≈ 1 (5.38) În consecinţă coeficienţii de debit sunt pentru: -secţiuni circukare:
=≈ ϕμ
∑ ++DL1
1
λξ (5.39)
-secţiuni dreptunghiulare:
∑ ++==
RL1
1
λξϕμ (5.40)
unde L = lungimea barabacanei, D =diametrul secţiunii circulare, R = raza hidraulică a secţiunii dreptunghiulare, ∑ = suma coeficienţilor tuturor rezistenţelor locale, λ = coeficientul rezistenţelor liniare, care depinde re rugozitatea pereţilor.
ξ
Muchiile de intrare pot fi ascuţite(vii), teşite sau rotunjite.Cu cât muchiile sunt mai bine rotunjite, fapt ce asigură o intrare lină în barbacane, coeficientul rezistenţelor locale scade şi evident că debitul de evacuare creşte. Coeficientul ξ = 0,05…..0,10.
Pentru calcule orientative, indiferent de natura pereţilor, se poate lua λ . 25,o≈Coeficienţii de debit pentru barbacane din beton se pot calcula cu formulele(D.L.Yarnel,
F.A.Nagler, S.M.Woodward, King Brater Lencaster) pentru: 1.Conducte circulare:
-cu muchie de intrare rotunjită:
2,1DL026.01,1
1
+=μ (5.41)
-cu muchie de intrare ascuţită(vie):
2,15,0
DLL31,01
1
++=μ (5.42)
2.Conducte dreptunghiulare: -cu muchie de intrare rotunjită:
25,1RL0045,005,1
1
+=μ (5.43)
-cu muchie de intrare ascuţită(vie):

25,15,0
RL0045,0R48,01
1
++=μ (5.44)
Pe baza acestor formule sunt întocmite tabele pentru coeficienţii de debit. 5.3.DEVERSOARE. 5.3.1. DEFINITII. Deversoarele sunt deschideri practicate la coronamentul construcţiilor hidrotehnice
transversale, peste care trece apa în curgere cu suprafaţă liberă. În mod obişnuit deversoarele sunt amplasate în partea centrală a construcţiei, ele
limitând frontul de scurgere al apelor şi dirijează curentul după o direcţie definită.
Fig.5.8. Parametrii geometrici şi hidraulici ai deversoarelor.
Parametrii geometrici ai deversoarelor sunt (fig.5.8): -Creasta sau pragul deversorului, care este porţiunea din coronament BC peste care se
scurg apele. -Umerii deversorului AB şi CD, care încadrează şi mărginesc lateral lama deversantă. Parametrii hidraulici ai deversoarelor sunt (fig.5.8): -Forma deversorului ABCD în profil transversal. -Forma pragului “a”. -Lăţimea pragului “a”, care este egală cu grosimea construcţiei la coronament în zona
deversată. -Sarcina deversorului H. -Sarcina totală a deversorului H0:
g2V
HH2
000
α+= (5.45)
Teoretic, suprafaţa apei în apropierea deversorului capătă o formă curbă, care se racordează la infinit cu suprafaţa liberă a apei din amonte, racord care se consideră că se realizează practic la distanţa . H3d ≥
-Lăţimea deversorului b măsurată după direcţia muchiei pe care se scurge apa. -Înălţimea pragului în amonte Ym care este măsurată pe verticală între pragul
deversorului şi nivelul terenului în momentul execuţiei construcţiei. La lucrările hidrotehnice transversale pentru corectarea torenţilor, se ia raportul:
81

5,2.....5,0YH
m
= (5.46)
raport denumit înălţimea relativă a deversorului. Curgerea în amonte de deversor se consideră în regim lent, caz în care viteza de acces
V0 în funcţie de mărimea acesteia poate fi sau nu considerată ca parametru independent determinant.
Datorită diferenţei de sarcină ce există dintre nivelele amonte şi aval, curgerea este rapidă şi neuniformă, firele de curent având o curbură pronunţată, formându-se astfel lama deversantă.
5.3.2.CLASIFICAREA DEVERSOARELOR Clasificarea deversoarelor se poate face după diverse criterii, luând în considerare
factorii importanţi care influenţează curgerea peste deversor. Astfel: a)După forma secţiunii de curgere (forma conturului) avem:
-deversoare poligonale: dreptunghiulare, triunghiulare, trapezoidale (fig.5.9a) utilizate la pragurile şi barajele din zidărie de piatră cu mortar de ciment şi din beton.
Fig.5.9. Deversoare poligonale şi curbilinii.
-deversoare curbilinii: arce de cerc, elipsă, parabolă (fig.5,9b),folosite la
pragurile din zidărie de piatră uscată, cleonaje,etc. b)După raportul a/H dintre grosimea pragului a şi sarcina de apă H în deversor. Acest raport este criteriul principal de clasificare a deversoarelor, deoarece determină
regimul hidraulic de funcţionare al deversorului. Se deosebesc trei tipuri de deversoare: 1.Deversoare cu prag subţire cu raportul a/H≤ 0,67 la care lama de apă se desprinde
din dreptul muchiei amonte a pragului, pe care nu-l mai atinge în timpul deversării (fig.5.10a)
Fig.5.10. Deversoare cu prag subţire, gros şi lat.
2.Deversoare cu prag gros cu raportul 0,67<a/H≤ 2,5 denumite şi deversoare cu
profile practice, la care pânza inferioară a lamei deversante atinge numai instantaneu suprafaţa orizontală a pragului (fig.5.10b).
3.Deversoare cu prag lat cu raportul a/H>2,5 (fig.5.10c), la care apa curge un anumit timp pe suprafaţa orizontală a pragului, fapt ce determină o subţiere a lamei deversante, urmare creşterii vitezei în zona de deasupra pragului, curentul fiind gradual variat în porţiunea centrală.
La deversoarele clasice grosimea pragului era de 2…3 m. Această grosime, la barajele pentru corectarea torenţilor a scăzut la 0,5 m, astfel încât pentru raportul a/H se utilizează valorile 0,25…1,50, ceea ce corespunde deversoarelor cu prag subţire şi prag gros.
82

c)După felul contracţiei avem (fig.5.11): 1.Deversoare cu contracţie laterală la care b < B. 2.Deversoare fără contracţie laterală la care b = B.
Fig.5.11. Deversoare cu şi fără contracţie laterală
Fig.5.12.Deversoare cu prag poligonal şi prag curb
d)După profilul pragului avem: 1.Deversoare cu prag poligonal (fig.5.12a). 2.Deversoare cu prag curb (fig.5.12b). e)După forma lamei deversamte avem: 1.Deversoare cu lama deversantă liberă (fig.5.13a), când aceasta are două pânze. 2.Deversoare cu lama deversantă aderentă (sprijinită) (fig.5.13b), când lama aderă şi
se sprijină pe paramentul aval. f)In raport cu dispoziţia lor în plan: 1.Deversoare frontale care sunt normale pe direcţia curentului de apă. 2.Deversoare înclinate faţă de direcţia curentului. g)După nivelul apei din bieful aval: 1.Deversoare libere (neînecate), când nivelul apei din bieful aval este sub nivelul
pragului deversorului şi nu influenţează curgerea prin deversor (fig.5.14a).
fig.5.14.Deversoare neînecate şi înecate.
2.Deversoare înecate parţial sau total (fig.5.14b),când nivelul apei din aval depăşeşte
nivelul pragului deversorului şi influenţează curgerea prin deversor. 5.3.3.DEBITUL DEVERSOARELOR CU PRAG SUBŢIRE. 5.3.3.1. DEVERSORUL DREPTUNGHIULAR. FORMULA GENERALĂ A DEDITULUI PRIN DEVERSOR. Dacă se consideră un orificiu cu secţiune dreptunghiulară, la care suprafaţa liberă a apei
coincide cu muchia superioară a orificiului, atunci acesta se transformă într-un deversor dreptunghiular cu prag subţire având adâncimea H2 = H, deoarece H1 = 0 (fig.5.15).
83

Fig.5.15.Deversor dreptunghiular cu prag subţire
Astfel din relaţia (5.23) pentru un orificiu dreptunghiular, rezultă formula debitului
dedusă de Weissbach pentru deversorul dreptunghiular, pentru α0 = 1:
⎥⎥⎥
⎦
⎤
⎢⎢⎢
⎣
⎡
⎟⎟⎠
⎞⎜⎜⎝
⎛−⎟⎟
⎠
⎞⎜⎜⎝
⎛+=
23
20
23
20
g2V
g2V
Hg2b32Q μ (5.45)
Neglijându-se viteza de acces, respectiv termenul /2g, se obţine formula uzuală
dedusă de Poleni şi Du-Buat:
20V
gH2bH32Hg2b
32Q 2
3
μμ == (5.46)
Dacă se ia în considerare viteza de acces V0 debitul este:
23
0Hg2b32Q μ= ; H0= H +
g2V 2
00α (5.47)
Notând cu: μ32m = denumit coeficient de debit
A = bH aria deversorului în plan vertical relaţia (5.46) devine:
gH2mAQ = (5.48) care reprezintă formula generală a debitelor prin deversoare. Această formulă este valabilă numai pentru baraje şi praguri unde înălţimea utilă
Ym>0. Pentru traverse la care Ym= 0, pragul fiind la nivelul terenului, debitul se determină cu
formula utilizată la canalele de evacuare (formula lui Chézy), considerându-se mişcarea uniformă, formula corectată cu coeficientul de contracţie ε, datorat umerilor deversorului:
RiACQ ε= (5.49)
Din formulele uzuale rezultă că capacitatea de evacuare a deversorului depinde de
coeficientul de debit m , de lăţimea deversorului b şi sarcina în deversor H sau H0.
84

Pentru coeficientul de debit se poate lua valoarea m = 0,40, ceea ce corespunde valorii μ = 0,60.
Coeficientul de formă m depinde însă de: -coeficientul de formă al deversorului m0, care este coeficientul de debit al deversorului
cu lama liberă, fără contracţie laterală, cu viteza de acces nulă, din experienţe şi diverse formule a rezultat m = 0,30…..0,60;
-coeficientul funcţie de viteza de acces a apei în deversor mv; -coeficientul de contracţie laterală ε ; -coeficientul de înecare al deversorului σ ; aşa încât:
m = m0.mv. σε . (5.50) Pentru deversoarele cu prag subţire neînecate (libere) fără contracţie laterală (b=B),
coeficientul de debit conform relaţiei lui Bazin este:
( ) ⎥⎥⎦
⎤
⎢⎢⎣
⎡
++⎟
⎠⎞
⎜⎝⎛ += 2
m
2
YHH55.01
H0045,06075,0
32m (5.51)
relaţie valabilă pentru: 0,5 < b < 2m; 0,1 < H <0,6m; 0,2 < Ym<2m. Relaţia (5.51) ia în considerare şi influenţa vitezei de acces şi poate fi extinsă cu
rezultate aproximative şi în afara domeniului ei de aplicare. Dacă este neglijată viteza de acces, coeficientul de debit este:
H003.0405,0
H0045,06075,0
32m +=⎟
⎠⎞
⎜⎝⎛ += (5.52)
La deversoarele dreptunghiulare libere, cu contracţie laterală (b < B), la care intervine
coeficientul de formă şi coeficientul de contracţie laterală, coeficientul de debit este dat de formula lui Hegley:
m=( ) ⎥
⎥⎦
⎤
⎢⎢⎣
⎡
++⎥
⎦
⎤⎢⎣
⎡⎟⎠⎞
⎜⎝⎛ −−+ 2
m
2
2
2
YHH.
Bb55,01.
Bb103,0
H0027,0405,0 (5.53)
Influenţa factorilor principali asupra capacităţii de evacuare a deversoarelor se pot
caracteriza în esenţă astfel: -Capacitatea de evacuare a deversorului creşte odată cu reducerea înălţimii utile Ym,
datorită creşterii vitezei de acces a apei pe deversor, urmare reducerii secţiunii vii (debitul fiind constant).
-La deversoarele cu prag subţire, creşterea sarcinii H , duce la scăderea coeficientului de debit, pe când la cele cu prag gros la creşterea acestuia.
-Creşterea grosimii pragului deversorului a, în anumite limite, micşorează coeficientul de debit. Deci grosimile reduse la coronament, duc la creşterea capacităţii de evacuare, simultan cu economii de materiale.
-Muchia vie(ascuţită) a pragului din amonte micşorează coeficientul de debit, iar cea rotunjită îl măreşte. După colmatarea totală a barajului efectele acestor forme sunt nule..
-Capacitatea de evacuare poate fi redusă şi de rugozitatea pragului, înclinarea deversorului faţă de direcţia curentului, profilul coronamentului, transportul de aluviuni grosiere, bolovani, flotanţi.
85

5.3.3.2. DEVERSORUL TRIUNGHIULAR. Deversoarele triunghiulare cu flancurile cu platbandă metalică, se utilizează pentru
măsurarea cu precizie a debitelor mici, de obicei sub 1 m3/s.
Fig.5.16. Deversor triunghiular
Debitul elementar este: gz2dAdQ μ= (5.54)
unde: dA =xdz; x=2(H – z) (5.55) Considerând coeficientul μ constant, prin
integrare se obţine debitul deversorului:
( )
⎟⎟⎠
⎞⎜⎜⎝
⎛−
=−== ∫∫
25
25
21
0
52
322
22
HHgtg
dzzzHgtgdQH
A
αμ
αμ
2
Q
(5.56)
25
Hg2tg158Q αμ= (5.57)
Pentru unghiul α = 450 (2α = 900) se obţine deversorul Thompson, având debitul:
25
Hg2158Q μ= (5.58)
Pentru μ = 0,5926 avem coefcientul de debit m= μ158 =0,316 iar
25
25
H4,1Hg2316,0Q ≅= (5.59) pentru 5 < H < 25 cm. Dacă se ţine seama de influenţa sarcinii în deversor şi a vitezei de acces, coeficientul de
debit este dat de relaţia lui Hegley pentru 0,1 < H <0,5 m:
⎥⎥⎦
⎤
⎢⎢⎣
⎡⎟⎟⎠
⎞⎜⎜⎝
⎛+⎟
⎠⎞
⎜⎝⎛ +=
2
m
d
AA
1.H002,0310,0m (5.60)
unde Ad = aria deversorului la nivelul sarcinii H; Am= suprafaţa udată a albiei în amonte.
5.3.3.3.DEVERSORUL TRAPEZOIDAL.
Pentru un deversor trapezoidal, liber, fără contracţie laterală având pragul de dimensiunea b, umerii acestuia înclinaţi faţă de verticală cu unghiul α , debitul este dat de suma debitelor unui deversor dreptunghiular de dimensiuni b, H, şi deversor triunghiular cu sarcina H şi unghiul la vârf 2α (fig.5.17).
86
Fig.5.17. Deversor trapezoidal.

25
23
Hg2tg158Hg2b
32Q αμμ += (5.61)
Notând cu: μ32m = şi μ
158m
54
= (5.62)
Relaţia (5.61) devine:
( ) 23
25
23
Hg2Htg8,0bmHg2mtg54Hg2mbQ αα +=+= (5.63)
Dacă intervine contracţia laterală de coeficient ε, acesta corectează lungimea pragului b, aşa încât debitul, când nu se ţine seama de viteza de acces, este:
( ) 23
Hg2Htg8,0bmQ αε += (5.64) Dacă se ia în considerare viteza de acces, în relaţia (5.64) în loc de H se ia H0. Pentru un deversor trapezoidal cu α =450, ε = 0,9 şi m=0,4, debitul este
Q = 1,77 ( ) 23
HH8,0b9,0 + (5.62)
Deversorul trapezoidal cu 41tg =α şi cu coeficientul de debit constant m=0,418,
denumit deversorul Cipoletti are debitul:
( ) 23
HH2,0b86,1Q += ε (5.63) Insă contracţia laterală este:
bH2,01−=ε (5.64)
aşa încât debitul este
23
bH86,1Q = (5.65) 5.3.4. DEBITUL DEVERSOARELOR CU PRAG GROS. Formulele de calcul pentru deversoarele cu prag gros (0,67 < a/H 5,2≤ ) sunt
asemănătoare ca tip cu cele de la deversoarele cu prag subţire. Parametrul principal este coeficientul de debit care trebuie adoptat, care variază în limite largi, (0,30….0,60), siguranţa acestora fiind mică, datorită numărului mare de factori care influenţează scurgerea prin deversor.
In practica de proiectare se pot folosi coeficienţii lui Certusov pentru: -deversoarele la care profilul pragului este dreptunghiular sau trapezoidal
m=0,40……0,43; -deversoarele la care profilul pragului este curbiliniu m = 0,45……0,49. Coeficientul de debit se poate stabili şi cu formule empirice. Astfel pentru deversoarele
frontale libere formula este: m = m0ε (5.66)
unde: m0 este coeficientul de formă al deversorului; ε este coeficientul contracţiei
laterale. Pentru deversoarele al căror prag au profil trapezoidal cu parament amonte vertical,
neînecat, fără contracţie laterală, coeficientul de formă m0 după Berezinski este:
87

m0 = 0,32 + ⎟⎠⎞
⎜⎝⎛ −
Ha5,25,0 (5.67)
iar coeficientul de contracţie laterală ε după acelaşi autor este:
⎟⎠⎞
⎜⎝⎛ −
+−=
Bb1
Bb.
YH3,0H1 43
m
ξε (5.66)
unde ξ este un coeficient cu valorile:
ξ =0,19 pentru deversoare cu muchia amonte ascuţită; ξ=0,10 pentru deversoare cu muchia rotunjită.
H este sarcina în deversor, Ym este înălţimea pragului, b lungimea crestei pragului, B lăţimea albiei la nivelul suprafeţei libere în bieful amonte al barajului.
Viteza de acces se poate neglija pentru valorile V0<0,75……1,0 m/s, sau dacă Am>Ad, Am este suprafaţa udată în bieful amonte al barajului, iar Ad aria secţiunii deversante aferente sarcinii H.
5.3.5. DIMENSIONAREA DEVERSOARELOR. La dimensionarea deversoarelor trebuie să se ţină seama de următoarele: -Deversoarele se dimensionează la debitul maxim de calcul Qd şi se verifică la debitul
maxim de verificare Qv. Debitul maxim de calcul Qd, este debitul corespunzător probabilităţii de funcţionare în
condiţii normale a lucrărilor, punând condiţia ca evacuarea acestui debit să se facă fără apariţia unor avarii sau perturbaţii nici în funcţionarea lucrărilor proiectate şi nici în funcţionarea lucrărilor de apărat.
Debitul maxim de verificare Qv, este debitul corespunzător probabilităţii de exploatare a lucrărilor în condiţii excepţionale, cu admiterea unor avarii şi perturbaţii, în funcţionarea lucrărilor proiectate şi a obiectivelor de apărat, de mică importanţă, care să poată fi remediate fără scoaterea din funcţiune a acestora,
Rezultă că debitul de calcul trebuie să fie evacuat în întregime prin deversorul barajului, iar debitul de verificare să fie evacuat parţial prin deversor şi parţial peste aripile deversorului, dacă acesta se poate limita la cel mult 0,10……0,30 m grosimea lamei deversante şi terenul din aval nu este predispus afuierii.
Fig.5.18. Debitul de calcul şi debitul de verificare.
-Aripile deversorului de la coronamentul barajului se înclină spre maluri cu 5…15%,
pentru a limita lăţimea lamei deversante. -La barajele din beton şi din zidărie de piatră cu mortar de ciment se practică
deversoarele trapezoidale cu umerii având înclinarea de 1/1 (α=450). In albiile înguste, cu debit mare, se utilizează deversoare trapezoidale cu şi deversoare dreptunghiulare, pentru ca deschiderea superioară a deversorului b + Htgα să fie cel mult egală cu lăţimea radierului.
045≠α
88

-Profilul pragului deversorului, în mod obişnuit este trapezoidal cu muchiile tăiate, mai rar rotunjite.
-Dimensiunile deversorului rezultă din aplicarea formulelor aferente formei geometrice, în care se adoptă dimensiuni cunoscute şi necunoscute. La deversoarele trapezoidale cu unghiul α cunoscut, se adoptă ca dimensiune cunoscută fie deschiderea b , fie sarcina în deversor H, evident pentru un coeficient de debit cunoscut.
-Coeficientul de debit m fiind o funcţie complexă de formă şi dimensiunile deversorului, de deschiderea albiei în amonte, etc., dimensionarea se face prin încercări succesive. Astfel de exemplu se admite un anumit coeficient de debit m şi o anumită deschidere b ,cu ajutorul lor se aproximează sarcina în deversor; prin încercări succesive se obţin dimensiunile deversorului care asigură evacuarea debitului de caicul dat. Valoarea sarcinii de calcul H=Hd este bine să fie multiplu de 0,25 m, ceea ce facilitează utilizarea fără interpolări a tabelelor şi graficelor pentru dimensionare.
-La lucrările importante este bine ca raportul H/b să fie cât mai apropiat de cel economic. O sarcină H sub 0,50 m, creiază pericolul trecerii apelor peste aripi, la torenţii cu aluviuni grosiere.
-Intre geometria deversorului şi geometria barajului există o strânsă interdependenţă. Astfel cei doi factori H şi b, influenţează dimensiunile lucrărilor din bieful aval, volumul întregii construcţii hidrotehnice, etc.
-Odată dimensionat deversorul la debitul de calcul, se determină sarcina de verificare Hv (fig.5.18), Hv=Hd + ΔΗ corespunzătoare debitului de verificare. In cazul trecerii debitului de verificare, trebuie luate în considerare şi deversoarele triunghiulare care se formează de o parte şi de alta de deversorului central (care este depăşit cu ΔΗ).
5.4. DISIPATOARE HIDRAULICE DE ENERGIE. 5.4.1. AFUIEREA BARAJELOR. Lama deversantă, formată din apă şi aluviuni, în căderea sa violentă, prin impactul
asupra terenului din aval de baraj, produce escavaţii în acesta, denumite pâlnii de eroziune (fig.5.19).
Fig.5.19. Pâlnia de eroziune.
Pe măsura creşterii dimensiunilor acestei pâlnii, aceasta poate duce la subminarea
(afuierea) barajului, diminuând sau anulând stabilitatea acestuia. Surplusul de energie cinetică care provoacă afuierea terenului din aval este dat de
relaţia:
g2VV
QE2
a2
dc
−= γΔ ( kNm) (5.67)
89

unde : γ = greutatea specifică a apei cu aluviuni (kNm-3); Q=debitul lamei deversante (m3s-1); Vd=viteza medie de deversare a apei peste baraj (ms-1); Va = viteza medie a apei în bieful aval (ms-1); g=acceleraţia gravitaţională (ms-2).
Această energie se consumă pentru erodarea fundului albiei şi respective frecarea interioară între particulele de lichid.
Pâlniile de eroziune pot fi produse în anumite situaţii şi de curgerea apelor subterane, care antrenează particulele solide, fenomen cunoscut sub denumirea de sufozie sau eroziune internă sau antrenare hidrodinamică. In acest caz sunt necesare lucrări speciale.
Din punct de vedere hidraulic, problema se fundamentează pe formarea saltului hidraulic, imediat în aval de secţiunea contractată, şi pe scăderea energiei cinetice până la valoarea minimă, corespunzătoare adâncimii critice.
5.4.2 DEFINIŢII. PĂRŢI COMPONENTE. Disipatoarele hidraulice de energie sunt construcţii speciale, care se execută în bieful
aval al barajelor, făcând corp comun cu acesta, cu scopul disipării energiei cinetice suplimentare, pentru evitarea complectă a fenomenului de afuiere, sau dacă acest lucru nu este posibil, să fie îndepărtată cât mai mult pâlnia de eroziune faţă de amplasamentul fundaţiei lucrării transversale.
Disipatoarele de energie sunt de diverse tipuri. In funcţie de aceste tipuri se pot distinge următoarele construcţii componente:
-Radierul amplasat la baza elevaţiei paramentului aval, în dreptul deversorului. -Zidurile de gardă (de apărare) care încadrează lateral radierul. -Dinţii disipatori de energie amplasaţi pe radier. -Contrabaraj; prag; traverse. -Pinten terminal al radierului încastrat în teren. -Risberme de diverse tipuri. 5.4.3. TIPURI DE DISIPATOARE. 5.4.3.1. DISIPATOARE CU PRAG TRANSVERSAL PE RADIER (CONTRABARAJ). Acest tip este format dintr-un bazin pentru liniştirea apei denumit bazin disipator, în
cuprinsul căruia scurgerea rapidă (torenţială) să fie înecată în salteaua de apă dintre baraj şi prag (contrabaraj).
Se deosebesc următoarele forme:
Fig.5.20. Disispatoare cu prag transversal pe radier.
-disipator sub forma unei adâncituri în radier (fig.5.20.a); -disipator cu prag (contrabaraj) special (fig.5.20.b) -disipator combinat (mizt) (fig.5.20.c).
90

Fig.5.21. Curgerea în disipator.
Aceste tipuri s-au folosit în anii 1950-1960, fără însă a da rezultatele asteptate. Aceasta
datorită colmatării cu aluviuni a bazinelor disipatoare şi a subminării în aval a contrabarajului, necesitând repetate reparaţii.
Pentru îmbunătăţirea caracteristicilor bazinelor, Bradley-Peterka prevăd praguri dinţate care fracţionează curentul, micşorând energia cinetică.
5.4.3.2. DISIPATOARE CU TREPTE DE CĂDERE (DISIPAT0R ÎN CASCADĂ). Disispatorul de aceste tip este realizat dintr-un radier cu una sau mai multe trepte de
cădere (fig.5.22).
Fig.5.22. Disipator în cascadă.
In practică, nici acest tip nu a dat rezultatele scontate, deoarece nu asigură o reducere
substanţială a vitezei, iar treptele de cădere produc neregularităţi de scurgere, concentrează şocul asupra radierului fapt ce duce la avarii.
Când însă condiţiile de teren impun acest tip, este bine ca înălţimea treptelor să fie cât mai redusă.
Acet tip de disipator este necesar pe canalul de scurgere, unde condiţiile de pantă le impun.
5.4.3.3. RADIER CU DINTI DISIPATORI DE ENERGIE. În urma cercetărilor şi studiilor pe modele de laborator, a verfificărilor experimentale,
s-a ajuns la concluzia că dispatoarele eficiente sunt radierele cu dinţi disipatori de energie (fig.5.1) şi (5.25).
Dinţii disipatori de energie fac corp comun cu radierul, au o anumită formă, anumite dimensiuni şi o anumită dispoziţie în plan. In mod obişnuit pot fi dispuse pe un singur rând sau două rânduri în alternanţă.
91

5.4.3.4. ALTE TIPURI DE DISIPATORI DE ENERGIE. -Radier fără dinţi disipatori de energie, dar cu zidurile de gardă dispuse converegent şi
racordate la canalul din aval. -Traverse de consolidare amplasate în albie în aval de baraj, în locul radierului, sau
imediat în aval de radier. -Risberme din blocaje de piatră, fascine, gabioane, etc. 5.4.4. DIMENSIONAREA DISIPATOARELOR DE ENERGIE. 5.4.4.1. PARAMETRII PRINCIPALI. Construcţiile care alcătuiesc disipatoarele de energie depind de următorii parametri
principali: -lungimea de bătaie a lamei deversante; -adâncimea curentului în secţiunea contractată; -lungimea şi lăţimea radierului; -înălţimea zidului de gardă; -elementele confuzorului. 5.4.4.2. LUNGIMEA DE BĂTAIE A LAMEI DEVERSANTE. Lungimea de bătaie a lamei deversante este lungimea măsurată pe orizontală, de la
creasta deversorului până la punctual în care lama deversantă atinge radierul, acolo unde există, sau fundul natural al albiei din bieful aval.
Pentru un baraj cu un deversor cu prag gros, şi bieful aval orizontal, dacă se ia ăn considerare mişcarea în vid unei particule de lichid a pânzei interioare şi exterioare a lamei deversante (fig.5.23), ecuaţiile parametrice sunt:
Fig.5.23. Traiectoria teoretică a pânzelor lamei decersante la un deversor cu prag gros
92
x = V.t ; y = 2gt21 (5.68)
Prin eliminarea parametrului timp t,
ecuaţia traiectoriei pariculei, care este o parabolă, are forma:
ygV2x
22 = (5.69)
Din relaţia (5.69) pentru:
y = Ym lungimea de bătaie a pânzei interioare este: gY2
Vl mbi = (5.70)
y = Ym+H lungimea de bătaie a pânzei exterioare este: g
)HY(2Vl m
be+
= (5.71)
În realitate traiectoria lamei deversante este diferită de cea teoretică. În practică lungimea de bătaie a lamei deversante se determină cu formule empirice,
deduse experimental.

Fig.5.24. Lungimea de bătaie a lamei deversante la deversor cu prag subţire.
Pentru determinarea lungimii de bătaie a lamei deversante M.D.Certusov (1966)
propune următoarele relaţii (fig.5.24): -Pentru deversoarele cu prag subţire, la care lungimea de bătaie lb se măsoară de la
muchia amonte a pragului, formula este: )H45,0Y(H38,1H33,0l 000b ++= (5.72)
-Pentru deversoarele cu prag gros, la care lungimea de bătaie lb se măsoară de la muchia aval a progului, avem:
)H33,0Y(H33.1l 0c0b += (5.73) unde: H0 = sarcina totală în deversor; Yc = înălţimea pragului deversorului de la
orizontala ce trece prin punctul unde lama deversantă atinge radierul sau patul natural al albiei, din bieful aval.
Înălţimea Yc poate fi egală sau mai mare decât înălţimea utilă Ym. În mod obişnuit radierele sunt înclinate, adică Yc > Ym.
Determinarea lui Yc se poate face prin metoda încercărilor succesive. Asfel la prima încercare se ia Yc1 = Ym şi se obţine o lungime de bătaie lb1. La a doua încercare înălţimea Yc2 se ia corespunzător lungimii lb1, după care se stabileşte prin calcul o nouă lungime lb2, ş,a.m.d. Aproximarea se consideră satifăcătoare când .ll 1bnbn +≅
Calculul prin încersări succesive se poate elimina prin exprimare înălţimii Yc în fucţie de:
-panta radierului, care în mod curent este egală cu panta albiei din aval ia = tgθ; -lungimea de bătaie a lamei deversante lb; -înălţimea utilă a barajului Ym. -după caz grosimea coronamentului în zona deversată a.
abmmc ilYYYY +=+= Δ (5.74) Efectuându-se operaţiile necesare, se obţin ecuaţiile de gradul II, care dau direct
lungimea de bătaie a lamei deversante. -Pentru deversoare cu prag subţire:
0)H75,0Y90,1(Hl)i90,166,0(Hl 0m0ba02b =+−+− (5.75)
-Pentru deversoare cu prag gros: 0)H53,0ai77,1Y77,1(HliH77,1l 0am0bao
2b =++−− (5.76)
5.4.4.3. ADÂNCIMEA CONTRACTATĂ. Lama deversantă în contact cu radierul se contractă, după care urmează saltul hidraulic.
Adâncimea curentului din secţiunea contractată condiţionează amplasamentul şi dimensiunile dinţilor disipatori de energie, cât şi lungimea radierului.
93

Adâncimea contractată se determină cu ecuaţia lui Bernoulli (fig.5.25), între secţiunile situate imediat în amonte de baraj (0-0’) şi secţiunea contractată din aval pe radier (C-C’).
Fig.5.25. Adâncimea contractată şi lungimea radierului.
Energia specifică a secţiunii contractate T0 este:
T0 = Yc + H0 = hc+ ∑ −+ CrO
2cc h
g2Vα
(5.77)
unde Yc = înălţimea de la baza secţiunii contractate până la pragul deversorului; H0=sarcina totală în deversor; αc = coeficientul lui Coriolis în seccţiunea contractată; Vc = viteza medie a curentului în secţiunea contractată; Σht0-C = pierderea totală de sarcină între cele două secţiuni.
Dacă se neglijează pierderile de sarcină liniare dintre cele două secţiuni, pierderea totală de sarcină este egală cu pierderea de sarcină locală:
g2Va
hh2
cclC0t ξΣ =≅− (5.78)
bilanţul energetic devine:
T0=hc+ g2V 2
ccα+ hl = hc + ( ξ
α+1
g2V 2
cc ) = hc + 2
2cc
g2Vϕ
α (5.79)
luând în considerare coeficientul de viteză de viteză ξ
ϕ+
=11
c de unde obţinem 2
11ϕ
ξ =+
Insă debitul Q = AcφcVc de unde 2c
2c
22
c AQV
ϕ= aşa încât:
T0 = hc + 2c
2c
2c
Ag2Qϕ
α (5.80)
unde Ac este suprafaţa udată a secţiunii contractate, care este funcţie de adâncimea contractată hc.
Din relaţia (5.80) rezultă:
( )c0c
cc hTg2
QA
−=ϕ
α (5.81)
94

Suprafaţa udată Ac = f(hc), ecuaţia (5.81) se rezolvă prin metoda încercărilor succesive.
Pentru o secţiune dreptunghiulară, paramentul zidurilor de gardă fiind vertical, suprafaţa udată este Ac = brhc.
Dacă lăţimea radierului este egală cu lăţimea crestei deversorului, adică br = b, atunci:
( )c0c
cc hTg2
qh
−=ϕ
α (5.82)
unde: q = bQ (m3/s.m) (5.83)
este debitul specific. Dacă forma dreptunghiulară a secţiunii radierului are baza mai mare ca cea a
deversorului, fapt ce duce la evazarea lamei şi la o reducere a adâncimii contractate, debitul specific este dat de relaţia (Certusov):
q = br l1,0b
Q+
(5.84)
unde lb = lungimea de bătaie a lamei deversante. Pentru o secţiune trapezoidală suprafaţa udată este:
Ac=brhc+m =hc(br+mhc) (5.85) 2ch
unde m este coeficientul de taluz al paramentului interior al zidului de gardă. Dacă br = b, din relaţia (5.81) adâncimea contractată este:
( )( )2cc0c
cc
mhbhTg2
Qh
+−=ϕ
α (5.86)
Dacă br>b caz în care lama deversantă se evazează, atunci lăţimea la baza secţiunii contractate, care se ia în calcul (Certusov) este:
br= bc =(b + 0,8Htgα) + 0,1. lb (5.82) unde α = unghiul format de umerii deversorului cu verticala.
Pentru determinarea adâncimii contractate pin încercări succesive, prima încercare se efectuiază cu hc = 0, la radicalul de la numitor, şi se obţine o mărime hc1, apoi se introduce acesta sub acelaşi radical şi se obţine hc2. Operaţiunea se repetă până când se obţine relaţia de egalitate bcn bcn+1. ≅
Adâncimea contractată se poate determina expeditiv folosind nomograma din figura (5.26).
95

Fig.5.26. Nomograma pentru determinarea adâncimii contractate pentru secţiunidreptunghiulare şi trapezoidale (Gaspar 1970).
5.4.4.4. DIMENSIUNILE RADIERULUI.
Lăţimea radierului br trebuie să fie cel puţinegală sau mai mare ca lungimea crestei deversorului b, adică br b. ≥
Lungimea radierului (Lr) este delimitată în amonte de intersecţia radierului cu paramentul aval al barajului (baza elevaţiei aval a barajului Yv), şi după caz, de pintenul terminal sau de confuzor. Această lungime este funcţie de lungimea de bătaie a lamei deversante la care se adaugă o lungime suplimentară de racordare în mod constructiv (fig.5.25).
-La barajele de priză, la care în general nu se prevăd dinţi disipatori de energie, lungimea de racordare este cel puţin dublul adâncimii contractate, este:
-pentru deversoare cu prag subţire: Lr = lb – (a + λYv) + 2hc (5.83)
96

-pentru devrsoare cu prag gros: Lr = lb – λYv + 2hc (5.84)
Dacă se prevăd dinţi disipatori de energie, în aceste relaţii se adaugă lungimea corespunzătoare ld.
-La barajele care nu sunt priză de canale, lungimea radierului este formată din suma lungimii de bătaie plus lungimea dinţilor disipatori, plus lungimea suplimentară Yv + H.
-pentru deversoare cu prag subţire: Lr = lb + Yv(1 – λ) + H – a + ld (5.85)
-pentru deversoare cu prag gros: Lr = lb + Yv(1 – λ) + H + la (5.86)
unde: a
amv i1
aiYY
λ−+
= (5.87)
Yv este elevaţia aval, iar ialbie = iradier. Relaţia (5.67) este valabilă şi pentru barajele cu priză. Lungimea radierului pentru cazul din figura (5.25) este:
Lr=lb-(a+λYv)+2hc+d1+4hc+d2+(1,5…2,0m (5.88) unde d1 şi d2 sunt dimensiunile de la baza dinţilor disipatori.
5.4.4.5.DIMENSIUNILE DINŢILOR DISIPATORI. In general, dinţii disipatori de energie au forma de prisme dreptunghiulare sau
trapezoidale. Studiile au arătat că efectul de disipare a energiei cinetice suplimentare este maxim,
când se aplică dinţilor disipatori următoarele condiţii privind amplasarea în plan şi înălţimea acestora:
-Rândul de dinţi din amonte se amplasează la distanţa 2hc , în aval de secţiunea contractată, înălţimea acestora fiind egală cu hc. -Rândul al doilea, amplasat în aval de primul rând de dinţi, se amplasează la distanţa de
4hc de la rândul din amonte, înălţimea acestora trbuie să fie egală cu (1,25…1,30)hc. 5.4.4.6. INALŢIMEA ZIDURILOR DE GARDĂ. Zidurile de gardă trebuie să satisfacă atât condiţia hidraulică de încadrare a apei în
radier, cât şi atunci când este cazul, de ziduri de sprijinn a malurilor albiei. Dezideratul hidraulic este satisfăcut dacă înălţimea zidului de gardă Yzg este:
Yzg = Yd + 0,6H (5.89) unde Yd = înălţimea dinţilor disipatori din primul rânmd (amonte); H = sarcina în deversor.
Condiţia de stabilitate la înpingerea pământului rezultă din dimensionarea corespunzătoare a zidului de gardă.
5.5. CONFUZOARE. 5.5.1.DEFINIT”IE. CONDITII DE RACORDARE. Confuzorul este construcţia din bieful aval, care racordează dispatorul de energie al
barajului cu canalul, care tranzitează viitura în colector (fig.5.27). Forma confuzorului este o pâlnie convergentă. Soluţia optimă din punct de vedere hidraulic şi economic pentru această pâlnie este cea
care are unghiul φ faţă de axa de simetrie a confuzorului, denumit unghiul de confuzor, valoarea de circa 140 ( φ = 12.50….150).
97

Fig.5.27. Confuzorul. Este bine ca muchiile de racordare dintre confuzor să fie rotunjite, iar panta
longitudinală a radierului,confuzorului şi canalului să fie egale. Confuzorul este bine să fie coaxial cu direcţia de scurgere a apei din decersor. Dacă
această condiţie nu poate fi satisfăcută, se înclină în mod convenabil muchia deversorului, astfel încât evacuarea debitului ptin deversor să nu ducă la perturbaţii în regimul de curgere.
5.5.2. LUNGIMEA CONFUZORULUI. Din figura (5.27) lungimea confuzorului este dată de relaţia:
)bb(2tg2
bbL cr
crcf −≅
−=
ϕ (5.90)
unde: br = lăţimea radierului; bc = lăţimea canalului. 5.5.3. ÎNĂLTIMEA ZIDURILOR ÎN CONFUZOR. Înălţimea zidurilor confuzorului trebuie să fie cel putin egală cu adâncimea curentului
din confuzor, în care are loc remuul pozitiv. Adâncimea curentului în sceţiunile din confuzor se decetrmină cu ecuaţia lui Bernoulli
(fig.5.28) pentru mişcarea permanentă gradual variată.
98

Fig.5,28. Secţiunile de calcul în confuzor.
Calculul porneşte dela secţiunea contractată (C – C) ca secţiune de control unde
sarcina hidrodinamică faţă de planul de comparaţie (P.C.) este:
1C
2cc
cC d.ig2V
hH −++=α
; 2c
22
c AQV = ; Ac=f(hc) (5.91)
iar pentru secţiunea de calcul (1 – 1) este:
H1 = h1 + 1dc
211 h
g2V
−+α ; 2
1
22
1 AQV = ; A1=f(h1) (5.92)
unde hdc-1 este pierderea de sarcină liniară egală cu: hdc-1 = Jc-1dc-1 (5.93)
Panta hidraulică conform formulei lui Chézy este:
RCAQ
RCV
Lh
J 22
2
2
2d === (5.94)
Luând în considerare panta medie hidraulică pe sectorul de lungime L=dc-1, conform relaţiei (5.93) pierderea de sarcină liniară pe această lungime este:
1cJ −
hdc-1= 1c1
21
21
2
c2c
2c
2
dRCA
QRCA
Q21
−⎟⎟⎠
⎞⎜⎜⎝
⎛+ (5.95)
Conform echivalenţei energiilor specifice în lungul curentului,condiţia este: H1 = Hc (5.96)
de unde prin încercări succesive se determină adâncimea h1. Pentru următoarea secţiune de calcul (2-2), căreia îi corespunde planul de comparaţie,
iar secţiunea de control devine secţiunea (1-1), operaţiunile de mai sus se repetă pentru echivalenţa H2 = H1 şi se obţine adâncimea curentului h2. Astfel, în continuare se procedează pentru celelalte secţiuni.până la secţiunea finală a confuzorului, unde adîncimea curentului este hn.
La capătul confuzorului, înălţimea zidurilor trebuie să fie: Yzcf = hn + s (5.97)
99

unde s = 10…20 cm reprezentând o gardă de siguranţă. 5.6. CANALE. 5.6.1. DEFINITII. CONDITII HIDRAULICE ŞI CONSTRUCTIVE. Canalele sunt lucrări hidrotehnice care asigură dirijarea şi evacuarea apelor de
viitură pe reţeaua hidrografică, cele amplasate pe versanţi colectează şi evacuiază surplusul de apă de pe suprafeţele respective, către reţeaua hidrpgrafică.
Din punct de vedere hidraulic, evident şi economic, un canal este corespunzător, respectiv optim, când evacuiază un debit maxim. Aceasta depinde de:
-forma geometrică a secţiunii transversale; -panta canalului; -continuitatea (discontinuitatea) profilului longitudinal; -natura materialului de construcţie (rugozitatea); -regimul de funcţionare, etc.; Din punct de vedere constructiv, trebuie să fie asigurate condiţiile de stabilitate şi în
special cea la eroziune şi afuiere. 5.6.2. CANALE CU SECŢIUNI OPTIME DIN PUNCT DE VEDERE HIDRAULIC. O sceţiune este optimă din punct de vedere hidraulic, dacă pentru o surafaţă udată
dată, în condiţiile când panta şi rugozitatea albiei sunt constante, evacuiază debitul cel mai mare.
Din formula debitului:
iPAACRiACQ == (5.98)
rezultă că , pentru A, C, i, constant, debitul este maxim când raza hidraulică R este maximă, deci perimetrul udat P este minim.
100

Fig.5.29. Secţiuni optime din punct de vedere hidraulic: a)semicirculare, b)dreptunghiulare, c)trapezoidale, d)triunghiulare, e)parabolice.
Semicercul (fig.5.29a) este prin definiţie secţiune optimă. Secţiune optimă din punct de vedere hidraulic este: -dreptunghiul rezultat din jumătatea unui patrat circumscris unui cerc de rază egală
cu adâncimea curentului (fig.5.29b). -trapezul care corespunde semihexagonului circumscris cercului de rază egală cu
adâncimea curentului (fig.5.29c). -triunghiul isoscel drept înscris unui cerc de rază egală cu adâncimea curentului,
respectiv înălţimea triunghiului (fig.5.29d)-
-secţiunea parabolică la care suprafaţa udată este A = 2h3
24 , iar raza hidraulică
este R = h/2 (fig.5.29e). In practică se folosesc frecvent profilele dreptunghiulare şi trapezoidale. Secţiunea optimă a semihexagonului (fig.5.29c) , al cărui unghi al taluzurilor faţă de
orizontală este α = 600, rezultă din următoarele relaţii:
A = bh + h2ctgα ; b = αhctghA− ; P = b +
αsinh2 = )(f
sinh2hctg
hA α
αα =+− (5.99)
Prin derivare în raport cu α şi egalare cu zero rezultă:
101

0sin
cosh2sin
hddP
22 =−=αα
αα (5.100)
de unde: 06021cos =⇒= αα
In contextul folosirii frecvente a trapezului izoscel, nu întotdeauna este posibilă folosirea semihexagonului din diverse motive (de exemplu caracteristicile terenului natura materialelor de construcţie a taluzurilor, trecerea sub un pod, etc.).
Fig.5.30. Secţiune trapezoidală.
Se pune deci problema găsirii unei secţiuni trapezoidale în care pentru un coeficient unghiular dat m =ctgα, aceasta să fie optimă din punct de vedere hidraulic.
Rezultă că trebuie determinat acel raport β = b/h, pentru care la o suprafaţă udată A
dată şi un coeficient unghiular m = ctgα dat, perimetrul udat să fie minim. Suprafaţa udată este:
A=bh+h2ctgα=h(b+hctgα)=h(b+mh)=h2 =⎟⎠⎞
⎜⎝⎛ + m
hb
h2(β+m) (5.101)
iar perimetrul udat: 22 m1h2bctg1h2b
sinh2bP ++=++=+= αα
(5.102)
Notând cu: m’ = 2m12 + (5.103) Perimetrul udat este:
P = b + hm’ = h ⎟⎠⎞
⎜⎝⎛ + 'm
hb = h(β +m’) (5.104)
Prin diferenţierea relaţiilor (5.101) şi (5.104) în raport cu h şi β , se obţin următoarele ecuaţii : dA = 2h(β + m)dh + h2dβ = 0 (5.105) dP = (β + m’)dh + hdβ = 0 (5.106)
Din aceste ecuaţii rezultă că :
hdh)'m(
hdh)m(h2d 2
+−=
+−=
βββ (5.107)
aşa încât: 2(β + m) = β + m’ (5.108) de unde : βο = m’ – 2m = 2 ( )mm1 2 −+ (5.109) în care βο reprezintă raportul optim.
Rezultă că în afara trapezului izoscel cu α = 600 ( m=ctg )58,0≈α , oricare alt trapez, poate să reprezinte o secţiune optimă din punct de vedere hidraulic, cu condiţia ca lăţimea relativă a canalului β=b/h să fie egală cu βο, respectiv perimetrul udat să fie circumscris unui semicerc cu diametrul la suprafaţa liberă a curentului.
Notând cu ko = m’ – m, paeametrii geometrici ai secţiunilor trapezoidale optime (S.A.Munteanu 1968) sunt:
-Suprafaţa udată optimă (Ao): Ao= bh+mh2=h2(βο+m)=(m’-m)h2=koh2 (5.110)
-Ad\ncimea curentului optimă (ho):
ooo
bAk1h
β== (5.111)
-Perimetrul udat optim (Po): Po=b+m’h= Ak2h)'m( oo =+β (5.112)
-Raza hidraulică optimă (Ro): 102

Ak2
12
b2hR
ooo ===
β (5.113)
-Lăţimea curentului optimă la suprafaţa liberă (Bo):
Ak'mh'mh)m2(mh2b
sinh2B
ooo ==−+=+== β
α (5.114)
-Lăţimea optimă a albiei la bază (bo):
Ak
hbo
ooo
ββ == (5.115)
Εlemente pentru calculul parametrilor secţiunilor trapezoidale optime din punct
de vedere hidraulic (S.A.Munteanu 1968) Tabela 5.1.
m 0,00 0,25 0,50 0,58 0,75 1,00 1,25 1,50 2,00 m’ 2,000 2,062 2,236 2,309 2,500 2,828 3,202 3,606 4,472 β0 2,000 1,652 1,236 1,155 1,000 0,828 0,702 0,6ο6 0,472
1/β0 0,500 0,640 0,809 0,866 1,000 1,207 1,425 1,651 2.118 1/2β0 0,250 0,320 0,395 0,433 0,500 0,604 0,713 0,836 1,059
k0 2,000 1,812 1,736 1,732 1,750 1,828 1,952 2,106 2,472 2k0 4,000 3,623 3,472 3,464 3,500 3,657 3,903 4,211 4,944
2 0k 2,829 2,692 2,635 2,632 2,646 2,704 2,794 2,902 3,145
1/2 0k 0,354 0,371 0,379 0,380 0,378 0,370 0,358 0,345 0,318
m’/ 0k 1,414 1,532 1,697 1,755 0,890 2,092 2,292 2,485 2,844
β0/ 0k 1,414 1,160 0,938 0,877 0,756 0,613 0,502 0,417 0,300 5.6.3.DIMENSIONAREA CANALELOR. 5.6.3.1.CONDIŢII HIDRAULICE ŞI DE STABILITATE. Canalele folosite în cadrul lucrărilor de amenajare a bazinelor hidrografice torenţiale
trebuie să îndeplinească două principale condiţii: -Condiţia hidraulică, constă în asigurea evacuarii debitului maxim de viitură. Forma
secţiunii este bine să fie optimă din punct de vedere hidraulic. -Condiţia de stabilitate la eroziune. Acţiunea dinamică a curentului de apă asupra
fundului şi pereţilor canalelor poate provoca eroziuni periculoase,ducând la distrugerea acestuia.In consecinţă în afara dimensionării pur hidraulice, care să asigure un anumit debit, la dimensionare, respectiv verificare, trebuie să se ţină seama de condiţia de stabilitate la eroziune, dată de corelaţia ce trebuie să existe dintre materialul din care se execută canalul şi viteza medie a curentului, respectiv al efortului unitar tangenţial la perete.
5.6.3.2. PARAMETRII PRINCIPALI DE CALCUL. Parametrii principali necesari pentru dimensionarea canalelor sunt:
-coeficientul de rugozitate ρ sau n; -coeficientul de taluz m; -lăţimea canalului la partea inferioară b; -lăţimea relativă a secţiunii β=b/h; -panta longitudinală i=J; -viteza medie în secţiune V; -debitul maxim Q.
103

104
In funcţie de parametrii cunoscuţi şi necunoscuţi, pentru diverse cazuri de calcul, se folosesc metodele specifice aferente
5.6.3.3. STABILITATEA CANALELOR LA EROZIUNE - Stabilitatea canalelor la eroziune, este bazată pe două orientări principale: -O orientare mai veche, criteriul vitezei, care constă în stabilirea valorii maxime
aadmisibile vitezei medii a curentului, sub care se presupune că nu se produc eroziuni periculoase, în materialul din care este construit canalul.
-O orientare mai nouă, care ia în considerare efortul unitar tangenţial la perete, denumită şi efort unitar de antrenαρε sau forţă unitară de tărâre, sau impropriu forţă de antrenare.
.1.Criteriul vitezei medii a curentului.
.Viteza medie a curentului depinde şi de natura şi dimensiunile particulelor, cât şi de materialul din care este executat fundul şi pereţii albiei sau a canalului. Cum însă viteza curentului pe fundul albiei şi al pereţilor, care produc eroziune diferă de viteza medie din secţiune dată de relaţia V=Q/A, este evident că această viteză este o primă sursă de erori.
In tabela 5.2. sunt redate vitezele medii admisibile pentru diverse pământuri şi materiale.
Tabela 5.2 Viteze medii admisibile (m/s)
La adâncimea medie a curentului (m)
Natura pământului
sau materialului
Dmensiunea Particulelor
(mm) hmed=0,40 hmed=1,0 hmed=2,0 hmed=3,0 0 1 2 3 4 5 6
I. Pământuri omogene necoezive 1 2 3 4 5 6 7 8 9
10 11 12 13 14
Praf şi mâl Nisip fin “ mijlociu “~ mare Prundiş mărunt “ mijlociu “ mare Pietriş mărunt “ mijlociu “ mare Bolovani mici “ mijlocii “ mari Bolovâniş
0,005-0,050 0,05-0,25 0,25-1,00 1,0-2,5 2,5-5,0 5-10 10-15 15-25 25-40 40-75
75-100 100-150 150-200 peste 200
0,12-0,17 0,17-0,27 0,27-047
0,47-9,53 0,53-0-65 0,65-0,80 0,85-0,95
0,95-1,2 1,2-1,5 1,5-2,0 2,0-2,3 2,3-2,8 2,8-3,2
peste 3,2
0,15-0,2 0,21-0,32 0,32-0,57 0,57-0,65 0,65-0,80 0,80-1,00 1,00-1,20 1,2-1,4 1,4-1,8 1,8-2,4 2,4-2,8 2,8-3,4 3,4-3,9 peste3,9
0,17,0,24 0,24-0,37 0,37-0,65 0,65-0,75 0,75-0,90 0,90-1,10 1,10-1,30
1,3-1,6 1,6-2,1 2,1-2,8 2,8-3,2 3,2-3,9 3,9-4,5
peste 4,5
0,19-0,26 0,26-0,40 0,40-0,70 0,70-0,80 0.80-0,95 0,95-1,20
1,2-1,4 1,4-1,8 1,8-2,2 2,2-3,0 3,0-3,4 3,4-4,2 4,2-4,9
peste 4,9II. Pământuri coezive
În funcţie de conţinutul de particule fine, compactitate, indicele porilor şi greutatea volimetrică
1 2 3 4 5
Argile nisipoase grele “ “ uşoare Loessuri tasate Nisipuri argiloase Sol vegetal şi mâl
0,38-1,53 0,34-1,45 0,27-0,60 0,27-0,55 0,12-0,17
0,45-1,80 0,40-1,70 0,32-0,70 0,30-0,65 0,15-0,21
0,49-1,98 0,44-1,87 0,35-0,77 0,33-0,71 0,17-0,24
0,54-2,16 0,48-2,04 0,38-0,84 0,36-0,78 0,19-0,26
III. Căptuşeli din zidărie cu mortar de ciment, beton şi beton armat 1 2 3 4 5 6 7 8
Zidărie din cărămidă “ “ piatră moale “ “ “ de calitate mijlocie Beton marca 210 “ “ 170 “ “ 140 “ “ 110 “ “ 90
1,6 2,9 5,8 7,5 6,6 5,8 5,0 4,2
2,0 3,5 7,0 9,0 8,0 7,0 6,0 5,0
2,3 4,0 8,1 10,0 9,2 8,1 6,9 5,7
2,5 4,4 8,7 11,0 10,0 8,7 7,5 6,2

105
IV. Consolidări 1 2 3 4
Anrocamente cu piatră de 75-100 mm “ “ “ * 100-150 “ “ “ “ “ 150-200 “ “ “ “ “ peste 200 “
2,0-2,3 2,3-2,8 2,8-3,2 peste 3,2
2,4-2,8 2,8-3,4 3,4-3,9
peste 3,9
2,8-3,2 3,2-3,9 3,9-4,5 peste 4,5
3,0-3,4 3,4-4,2 4,2-4,9
peste 4,95 Anrocamente ăn cleonaje, în funcţie de mărimea pietrelor valorile de la 1,2,3,4, cresc cu 10%
6 7 8
9 10 11
12 13
Pavaj simplu- bolovani de râu de 15cm Idem – bolovani de râu de20 cm Pavaj dublu şi pavaj din blocuri de piatră regulate,cioplite şi cu suprafeţe drepte,pietre de 15cm Idem-cu pietre de 20 cm Gabioane Imbrăcăminţi din nuiele verzi şi consolidări din nuiele Brazde verzi aşezate pe lat “ “ “ în perete
2,5 2,9
3,1 3,6
până la 4,2
1,8 0,6 1,5
3,0 3,5
3,7 4,3
până la 5,0
2,2 0,8 1,8
3,5 4,0
4,3 5,0
până -5,7
2,5 0,9 2,0
3.8 4,3
4,6 5,4
până-5,9
2,7 1,0 2,2
Viteza la fund este mai mare la canalele mai puţn adânci. Aşa cum se vede din tabela
5.2. valorile maxime admisibile admisibile ale vitezei medii, se iau mai mari la canalele mai adânci decât la cele mai puţin adânci.
Canalele vechi în general, admit viteze mai mari decât canalele noi, datorită adaptării lor la dinamica curentului, depunerilor de materiale coloidale, sau dezvoltarea vegetaţiei.
Incărcarea apei cu aluviuni, prin natura lor influenţeză eroziunea. Astfel în cazul aluviunilor fine până la fracţiunea nisipului, exclusiv, se pot lua viteze mai mari ca în cazul transportului de nisip, pietriş, sau bolovăniş. Dacă apa de exemplu este încărcată cu nisip sau pietrş colturos, aceasta la o singură viitură cu viteze mici poate degrada puternic o îmbrăcăminte din beton.
2.Criteriul eforturilor tangenţiale unitare la perete. Criteiul vitezei medii maxime admisibile, deşi este răspândit în proiectare, neavând o
fundamentare teoretică, din motivele mai sus menţionate nu dă rezultate corespunzătoare. Criteriul eforturilor tangenţiale unitare la perete are la bază cercetările coordonate de
E.W.Lane (U.S.Bureau of Reclamation) din perioada 1937-1955, Ven Te Chow 1959, şi ulterior a altor cercetători.
a) Canale dreprunghiulare foarte largi. Pentru albiile dreptunghiulare foerte largi, se admite că raza hidraulică este egală
practic cu cu adâncimea curentului h. Pentru regimul de curgere uniform, efortul tangenţial mediu la perete τ0 este:
το = γ.h.i = ρ.g.h.i (5.116) admiţându-se ca ipoteză fundamentală de calcul distribuţia uniformă a efortului tangenţial το de-a lungul lăţimii albiei b .
b) Canale trapezoidale. Pentru secţiunile trapezoidale eforturile se consideră astfel: -efortul tangenţial nu se distribuie uniform pe perimetrul udat; -efortul tangenţial maxim pe taluzuri τ’οmax este mai mic decât efortul tangenţial maxim
pe fundul albiei τomax. Distribuţia eforturilor tangenţiale pe fundul albiei şi taluzuri adoptate de Lane şi Chow,
care s-au impus sunt redate în figura (5.31).

Fig.5.31. Distribuţia eforturilor tangenţiale în canale trapezoidale.
Eforturile unitare tangenţiale maxime sunt date re relaţiile:
-pentru fundul canalului: hiKmaxmaxo γτ = (5.117)
-pentru taluzurile canalului:
hiK 'max
'omzx γτ = (5.118)
Distanţa pe verticală d de la fund la este: 'maxoτ
d = Kdh (5.119) Parametrii Kmax, K’max şi Kd sunt coeficienţi de reducere. In tabela 5.3 sunt redate valorile acestor coeficienţi, în funcţie de lăţimea relativă a
albiei şi coeficientul unghiular al taluzurilor m = ctgα. Tabela 5.3
Secţiuni dreptunghiulare şi trapezoidale m 0 (dreptunghi) 3/2 2/1
b/h Kmax K’max Kd Kmax K’mx Kd Kmax K’max Kd
0,00 (triunghi) 0,000 0,565 0,3 0,000 0,650 0,3 1,00 0,372 0,468 1,0 0,780 0,695 - 0,780 0,730 - 2,00 0,686 0,686 1,0 0,890 0,735 0,2 0,890 0,760 0,2 3,0 0,870 0,740 1,0 0,940 0,743 - 0,940 0,760 - 4,00 0,936 0,744 1,0 0,970 0,750 0,2 0,970 0,770 0,2 6,00 - - - 0,980 0,755 - 0,980 0.770 - 8,00 - - - 0,990 0,760 0,2 0,990 0,770 0,2 Secţiuni triunghiulare
m 1/2 2/3 1/1 3/2 2/1 K’max 0,325 0,375 0,480 0,565 0,650
Kd 0,7 0,7 0,5 0,3 0,3
3. Efortul unitar tangenţial critic. Efortul unitar tangenţial critic τοcr este forţa unitară de antrenare la care particulele de
pământ încep să se deplaseze, să fie antrenate de curent prin tărâre. Efortul unitar critic se determină separat pentru fundul albiei si separat la taluzuri. a) Canale cu pământ necoeziv din particule grosiere. -Stabilitatea fundului canalului. Efortul unitar critic se poate exprima prin diametrul particulelor D75 (diametrul căruia
îi corespunde curba granulometrică 75% în greutate, de material de diametru inferior),admiţănd un coefficient de siguranţă de 0,8:
75ocr D8,0≈τ (5.120) în care D se ia în centimetri.
Relaţia (5.120) este valabilă pentru greutatea specifică a pămîntului γp=2560kgf/m3=25,11 kN/m3
Dacă γp real > γp se foloseşte un factor de corecţie: 106

81,911,2581,9
C prealc −
−=λ
(5.121)
în care γp real se ia în kN/m3. De exemplu dacă γp real = 25,997 kN/m3 valoarea factorului de corecţie este
Cc=1,058 , valoare cu care se multiplică efortul unitar critic τocr, din relaţia (5.120). 1,1≈Fundul canalului este stabil la eroziune dacă omxτ < τοcr. -Panta longitudinală a canalului. In cazul mişcării uniforme unde J=I=i, pentru un canal trapezoidal cu m, b, h, D75
cunoscuţi, condiţia de pantă longitudinală este:
hKD8,0
imax
75
γ< (5.122)
care se compară cu panta i obţinută la calculul taluzurilor, şi se ia valoarea cea mai mică. -Stabilitatea taluzurilor canalului. Considerăm o granulă de pământ de suprafaţă “ a” calculată ca front de atac, situată
pe taluzul unui canal având unghiul α faţă de orizontală (fig.5.32), unghiul taluzului natural (unghiul de ferecare interioară a pământului respectiv) fiind φ.
Pe porţiuea submersată a taluzului, se iau ăn considerare pe de o parte acţiunea fizică exercitată de apă asupra coeziunii aparente şi asupra altor elemente ale pământului, şi pe de altă parte, efortul tangenţial exercitat de curent la contactul cu taluzul, efort al cărui efect duce la reducerea valorii unghiului de frecare φ.
Fig.5.32. Forţele care acţionează asupra granulei.
Forţele care acţionează asu pra granulei sunt:
Gw = greutatea proprie a granulei sub apă, care se descompune în: μN = Gwcosαtgφ forţa care tinde să menţină granula pe taluz şi T = Gwsinα forţa care tinde să deplaseze granula pe linia de cea mai mare pantă a
taluzului. Dacă taluzul este omogen granulometric şi gravimetric, în starea de repaus a apei
condiţia de echilibru este: ϕαα tgcosGsinG ww ≤ iar la limită ϕα tgtg = (5.123)
Apa fiind în mişcare granula este solicitată şi de forţa de antrenare pe taluz Ft pe direcţia curentului egală cu:
Ft = a. (5.124) ,oτ
unde este efortul tangenţial longitudinal unitar la peretele taluzului. ,
oτIn momentul reuperii echilibrului, granula începe să se deplaseze pe o traiectorie
determinată de forşa rezultatntă R: 2
t2 FTR += = 2,
o2.
22w asinG τα + (5.125)
Condiţia de echilibru limită este şi ţinând seama de expresia (5.123), prin transformările necesare obţinem, efortul tangenţial unitar critic unitar pe suprafaţa taluzurilor canalului:
,ocr
,o ττ =
107

ϕαϕατ 2
2w,
ocr tgtg1tgcos
aG
−= (5.126)
-Stabilitatea fundului canalului. In mod analog se determină condiţia limită de echilibru pentru o granulă de aceiaşi
greutate în stare de submersie pe fundul albiei.
fw FtgG =ϕ unde ocrf .aF τ= aşa încât ϕτ tga
Gwocr = (5.127)
-Relaţia dintre eforturile unitare critice. Dacă notăm cu K raportul dintre şi ,
ocrτ ocrτ obţinem:
ϕαα
ττ
2
2
ocr
,ocr
tgtg1cosK −== (5.128)
denumit raport al forţei unitare de antrenare (Lane, Carter, Chow), important pentru proiectare. Factorul K poate fi determinat şi din graficul din figura (5.33).
Fig.5.33. Grafic pentru determinarea factorului K. -Unghiul de frecare interioară. Valorile unghiului de frecare interioară φ, în funcţie de diametrul granulelor D75 (in
mm), pentru pământurile necoezive grosiere, pentru , rezultă din graficul din figura (5.343), pentru particule: 1-foarte colţuroase; 2-mijlociu colţuroase; 3-puţin coţuroase; 4-puţin rotunjite; 5-mijlociu rotunjite; 6-foarte rotunjite.
mm5D ≥
108

Fig.5.34. grafic pentru determinarea unghiului φ. b)Canale trapezoidale de pământ necoeziv din particule fine . La aceste canale se neglijează efectul forţei T=Gwsinα. Pentru pământ necoeziv din particule fine, valorile efortului unitar tangenţial critic τοcr
sunt redate în tabela 5.4. Tabela 5.4.
τocr kgf/m2 Diametrul mediu al particulelor D50 mm
Specificaţie 0,1 0,2 0,5 1,0 2,0 5,0 Apă limpede 0,012 0,013 0,015 0,020 0,029 0,068 Apă cu puţine aluviuni fine
0,024
0,025
0,027
0,029
0,039
0,081
Apă cu multe sedimente fine
0,038
0,038
0,041
0,044
0,054
0,090
c)Canale trapezoidale din pământ coeziv.
La terenurile coezive, la care nu se pot lua în considerare dimensiunile particulelor, se recurge la indicele porilor şi gradul de compactitate. Pentru o determinare precisă a efortului critic este evident că trebuie luate în considerare şi alte proprietăţi ale pământurilor.
In tabela 5.5. sunt redate valorile efortului critic pentru pământuri coezive. Tabel 5.5.
τocr kgf/m2 Compactitatea şi indicele porilor (e)
Natura
pământului din care este
constituită albia
Foarte puţin compact
e=2,0,,,,,1,2
Puţin Compact
e=1,2,,,,,0,6
Compact
e=0,6,,,,,0,3
Foarte Compact
e=0,3,,,,,0,2 Argile nisipoase (nisip sub 50%)
0,020
0,077
0,160
0,308
Pământuri cu multă argilă
0,015
0,069
0,149
0,275
109

110
τocr kgf/m2 Compactitatea şi indicele porilor (e)
Natura
pământului din care este
constituită albia
Foarte puţin compact
e=2,0,,,,,1,2
Puţin Compact
e=1,2,,,,,0,6
Compact
e=0,6,,,,,0,3
Foarte Compact
e=0,3,,,,,0,2 Argile 0,012 0,061 0,137 0,259 Pământuri slab argiloase
0,010
0,047
0,104
0,173
5.6.3.4. CALCULUL CANALELOR. 1.Canale cu secţiuni trapezoidale optime din penct de vedere hidraulic. In calculele de dimensionare a canalelor trebuie avute în vedere întotdeauna cele două
criterii, cel hidraulic adică să asigure evacuarea debitului, şi cel de stabilitate prin nedepăşirea vitezei admisibile, respectiv a efortului tangenţial unitar critic.
In funcţie de parametrii cunoscuţi şi cei necunoscuţi se folosesc diverse metode de calcul.
Să considerăm următoarele cazuri: a) Se cunoaşte: debitul Q; materialul din care este construit canalul, respectiv viteza
admisibilă V şi coeficientul lui Chézy C; coeficientul de taluz m. Nu se cunosc parametrii h, b,B,P,R. In acest caz:
-Se determină suprafaţa udată necesară A = Q/V; -Se calculează parametrul m’ = 2m12 + ; -Se calculează parametrul k0 = m’ – m ; -Cu relaţiile (5.111)….(5.115) şi datele din tabela 5.1, se determină parametrii: h0,
bo,Bo,P0,R0,β0. -Se calculează din formula lui Chézy, panta canalului i = V2/C2R0 = Q2/A2C2R0 ,
asigurându-se stabilitatea la eroziune. b)Se cunosc parametrii n(ρ),m,β0,J,Q; nu se cunosc parametrii b,h,V. Pentru rezolvarea problemei (S.A.Munteanu 1968) se folosesc modulele de debit şi
viteză cât şi relaţiile (5.111)….(5.111), aplicând metoda grafo analitică, metoda prin aproximaţii succesive, sau metoda interpolării liniare.
c)Pentru dimensionare canalelor trapezoidale şi dreptunghiulare cu secţiune optimă din punct de vedere hidraulic sunt întocmite diagrame, dintre care menţionăm cele ale lui S,A.Munteanu şi I.Ciortuz (1963) şi R.Gaspar ş.a.(1965).
2. Canale cu secţiuni neoptime din punct de vedere hidraulic. Nu intotdeauna, datorită condiţiilor specifice de teren, se pot adopta canale cu secţiuni
optime din punct de vedere hidraulic. In acest caz calculul canalelor este in funcţie de parametrii cunoscuţi respectiv
necunoscuţi care determină metoda de calcul. Condiţia fiind aceiaşi de asigurare a evacuării debitului şi stabilităţii la eroziune.
In cazul secţiunilor complexe cu profil minor şi major (fig.5.35), calculul debitului se face prin însumarea debitului secţiunii centrale cu cele ale secţiunilor laterale
Dacă canalul în secţiune , are
rugozităţi diferite ni corespunzătoare perimetrelor Pi, viteza medie se calculează cu un coeficient de rugozitate echivalent ne
Fig.5.35. Secţiune de canal cu profil minor şi major.
PnP
n iie∑= (5.129)

formuă discutabilă ca valabilitate hidraulică O altă formulă a lui N.N.Pavlovski este mai justificată (S.A.Munteanu 1968) este:
21
iie P
nPn
⎥⎥⎦
⎤
⎢⎢⎣
⎡= ∑ (5.130)
3. Panta longitudinală a canalului. Panta canalului nu întotdeauna poate fi continuă,datorită faptului de foarte multe ori,
panta terenului it = tgθt este mai mare decât panta admisibilă a canalului ic = tgθc rezultată din calculele de dimensionare.
Soluţia care se adoptă in aceste cazuri este cea a canalelor în trepte. In funcţie de configuraţia terenului, respectiv a profilului longitudinal avem: a)Canale cu trepte de aceiaşi înălţime h (fig.5.36),caz în care numărul treptelor n
pentru o lungime de canal L este: ( )
htgtgL
hHn ct θθΔ −
== (5.131)
lungimea unei trepte fiind: nLl = (5.132)
Fig.5.36. Canal cu trepte de aceiaşi înălţime.
b)Canale cu trepte de înălţimi diferite hi.
Fig.5.37. Canal cu trepte de înălţimi diferite.
AB = AC – BC ; hi = li(tgθt,i –tgθc) = li(it,i – ic) (5.133)
ci,t
i,ti ii
hl
−= ; ∑= ilL (5.134)
111

112
5.7. EVAZOARE. Racordarea canalelor cu colectorul trebuie efectuată astfel încât să se obţină viteze şi
adâncimi cât mai mici la confluenţă, pentru a se reduce efectul de deformare a albiei părâului emisar.
La stabilirea soluţiilor trebuie avute următoarele: -Debuşeul perpendicular pe direcţia emisarului, are curentul deviat în direcţia de curgere
a emisarului printr-o evazare asimetrică a porţiunii finale de canal. -Folosirea unei pâlnii evazate şi apoi comprimate la capătul din aval, în scopul creşterii
efectului de disipare a enrgiei cinetice. -Pâlnie de racordare sub form de difuzor simetric cu un unghi de 300 şi respectiv 450, pe
o lungime egală cu de 10 ori înălţimea apei în canal, cu scopul micşorării adâncimii curentului şi implicit a vitezei acestuia. Pentru mişcarea permanentă şi uniformă, unghiul optim al pâlniei difuzor este 300.
-Mărirea artificială a rugozităţii cu blocuri de piatră sau din beton, de tipul celor utilizaţi la dinţii disipatori de energie pentru reducerea vitezei. Distanţa dintre blocuri în ambele direcţii se ia egală cu adâncimea din canal, iar înălţimea lor va fi egală cu jumătate din adâncimea apei în canal.
BIBLIOGRAFIE SELECTIVĂ 1.Butnaru N., 2000, Hidraulică, Editura Universităţii Suceava 2.Cioc D., 1983, Hidraulica, Editura Didactică şi Pedagogică Bucureşti 3.Clinciu I.,LazărN., 1997, Lucrări de Amenajare a Bazinelor Hidrografice Torenţiale Editura Didactică şi Pedagogică Bucureşti. 4.Clinciu I.,Lazăr N., 1999, Bazele amenajării torenţilor, Editura Lux Libris Braşov. 5.Deymier C,et al.,1994, Conception et calcul de barrages de correction torrentielle Centre National du Mashinisme Agricol du Genie Rural, Groupement de Grenoble 6.Gaspar R.,1970, Studii asupra unor tipuri de baraje de corectarea torenţilor realizate în perioada 1960-1970, I.C.A.S. Bucureşti 7.Grudnicki F.,1996. Corectarea Torenţilor, Universitatea Suceava 8.Hütte, 1995, Manualul Inginerului-Fundamente. Editura Tehnică Bucureşti 9.Manualul Inginerului vol.II, 1966, Editura Tehnică Bucureşti
10.Munteanu S.,et al.,1993, Amenajarea Bazinelor Hidrografice Torenţiale cu lucrări silvice şi hidrotenice,vol.II, Editura Academiei Române. 11.Normativ pentru proiectarea lucrărilor de Amenajarea Bazinelor Hidrografice Torenţiale,vol.II, 1995, I.C.A.S. Bucureşti. 12.Pavel D.,1950, Hidraulică teoretică ţi aplicată, Editura Tehnică Bucureşti.